-
Quantum chromodynamics (QCD) is a well-established theory of strong color interaction among quarks and gluons. Two major aspects of QCD are the asymptotic freedom (ultraviolet regime) [1, 2] and quark confinement (infrared regime) [3]. In asymptotic freedom, the quarks interact weakly at a short distance inside the hadrons. In contrast, at a large distance (or at low energy), the quarks are confined and never exist in isolation. In addition to color confinement, dynamical chiral symmetry breaking is another important property of low-energy QCD, which is related to the dynamical mass generation of quarks. It is well known that the QCD exhibits confinement and chiral symmetry breaking with a small number of light quark flavors
$ N_f $ . However, for larger$ N_f $ , it is believed that a critical value$ N^{c}_{f} $ exists, above which the chiral symmetry restores and quarks become unconfined [4–6]. This$ N^{c}_{f} $ value must be smaller than the upper limit of the critical value where asymptotic freedom appears to exist, i.e.,$ N^{A,c}_{f}= (11/2)N_c $ [2]; for$ N_c=3 $ with a gauge group$ SU(3) $ , this critical number is$ N^{A,c}_{f}=16.5 $ . Hence, the QCD theory is considered to be conformal in the infrared, guided by an infrared fixed point (i.e., a point at which the β-functions for the QCD couplings vanish); see for example for details [7–12]. The region$ N^{c}_{f}\lesssim N_f<N^{A,c}_{f} $ is often called the "conformal zone" [4, 13]. At or near the upper end$ (N_f \lesssim N^{A,c}_{f}) $ of the conformal zone, the infrared fixed point lies in the weakly interacting region and can be solved using perturbative techniques of QCD. In contrast, around the lower end$ (N_f \sim N^{c}_{f}) $ , the infrared fixed point shifts toward the strongly interacting region where the coupling is sufficiently strong as$ N_f $ decreases; thus, the system enters a phase in which the chiral symmetry breaks and quarks become confined. In this scenario, the perturbative approaches to QCD are inconceivable; thus, the non-perturbative techniques are useful tools. Lattice QCD simulations [5, 14–17], as well as the continuum methods of QCD [6, 18–22], in the fundamental$S U(3)$ representation emphasize that the chiral symmetry restoration and deconfinement phases occur when$ N_f $ reaches the conformal zone$ 8\lesssim N^{c}_f< 12 $ . QCD theory with a larger number of colors$ N_c $ in the fundamental$S U(N_c)$ representation also has a significant role in the infrared domain. Ref. [22] discussed that the chiral symmetry is dynamically broken above a critical value$ N^{c}_{c}\approx2.2 $ . The increasing$ N_c $ enhances the dynamical mass generation near and above$ N^{c}_{c} $ . A large$ N_{c} $ also effects the critical value of flavors$ N^{c}_{f} $ , that is,$ N^{c}_{f} $ shifts toward its higher values as$ N_{c} $ increases.In addition to
$ N_{c} $ and$ N_{f} $ , the infrared domain of QCD is also affected by the presence of heat baths. It is believed that at zero or low temperature T, the fundamental degrees of freedom of low-energy QCD are the color-singlet (confined) hadrons, whereas at high T, when T reaches its critical value$ T_c $ , the interaction becomes weaker, thus causing hadrons to melt into a new phase, where the quarks and gluons become the new degrees of freedom. The chiral symmetry is restored and deconfinement of quarks occurs in this new phase. Lattice QCD calculations [23–29], the Schwinger-Dyson equation [30–39], and other effective models of low-energy QCD [40–46] indicate that the nature of this transition is a crossover in the presence of a finite current quark mass m. Similarly, when the quark chemical potential μ increases, the same physical picture prevails but the nature of the phase transition changes from crossover to first-order at some point, which is known as the critical endpoint in the QCD phase diagram, often drawn in the$ T-\mu $ plane. Experimentally, there is a strong motivation toward the study of phase transitions in the Heavy-Ion Collision at the Large Hadron Collider (LHC) at CERN, the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory (BNL), and the Compressed Baryonic Matter (CBM) experiment. The study of low-energy QCD for higher quark flavors$ N_f $ and$ N_c $ also has a significant role in physics beyond the standard model (BSM), and its extension to the QCD phase diagram at finite T and μ, where different phases of QCD exist, i.e., quark-gluon plasma, quarkyonic matter, neutron star environment, and the color-flavor-locked region of the QCD phase diagram.Our aim and motivation of this work was to investigate the critical
$ N_c $ and$ N_f $ for the chiral symmetry breaking and restoration at zero T and finite T and μ. Furthermore, we are interested to draw the QCD phase diagram in the$ T-\mu $ plane for various$ N_c $ and$ N_f $ . We use the effective Nambu-Jona-Lasinio (NJL) model [47], dressed with the number of quark flavors$ N_f $ and in the fundamental$S U(N_c)$ representation in the Schwinger-Dyson equations framework. The NJL model has several features and is commonly used in the literature. Dynamical chiral symmetry breaking and its restoration are some of the main features of this model. However, it does not support the phenomenon of quark confinement.The remainder of this article is organized as follows: In Sec. II, we introduce the general formalism of the NJL model at
$ T=0 $ and at finite T and μ. In Sec. III, we discuss the numerical solution of the gap equation to study dynamical chiral symmetry breaking and its restoration for higher$ N_c $ and$ N_f $ values. In Sec. IV, we present the numerical solution of the gap equation for higher$ N_c $ and$ N_f $ and at finite T. In Sec. V, we depict the numerical solution of the gap equation at finite μ for various$ N_c $ and$ N_f $ . In Sec. VI, we sketch the phase diagram in the$ T-\mu $ plane for various$ N_c $ and$ N_f $ . Finally, in Sec. VII, we provide the summary and conclusions of this work. -
We begin the QCD in an effective manner through the NJL Lagrangian density [47]:
$ \begin{equation} {\cal L}=\bar{q} ({\rm i}\not {\partial}-m)q + \frac{G_0}{2}[(\bar{q}q)^2+(\bar{q} {\rm i}\gamma_5 \vec{\tau}q)^2], \end{equation} $

(1) where q and
$ \bar{q} $ represent quark and antiquark fields, respectively. Here,$\not \partial =\gamma_{\mu} \partial^{\mu}$ , where$ \gamma^{\mu} $ are the Dirac ($ 4\times4 $ ) gamma matrices, and$\partial^{\mu}= -{\rm i} p^{\mu}$ ($ p^{\mu} $ represents the four-momenta). Here, m is the bare light quark mass matrix, which may be equal to zero at the chiral limit. The four-fermion interaction in the square brackets contains a scalar and pseudoscalar interaction piece.$ \vec{\tau} $ represents the Pauli matrix acting in isospin space.$ G_0 $ is the dimensionful effective coupling constant that can be obtained by considering the Fierz transformation of the color-current–color-current interaction ($ -(\bar{q}\gamma^{\mu}\lambda^{\alpha} q)^{2} $ ) (see Appendix A.3 in [41] or the Appendix of this paper).Such a Lagrangian density Eq. (1) describes dynamical chiral symmetry breaking, which, in the Hartree (mean field) approximation can be triggered through the following gap equation:
$ \begin{equation} M=m-2G_0 \langle\bar{q}q\rangle \quad {\rm or} \quad \frac{M-m}{2G_0}=\langle\bar{q}q\rangle, \end{equation} $

(2) where M is the effective or dynamically quark mass, and
$ \langle\bar{q}q\rangle $ is the quark-antiquark condensate:$ \begin{equation} \langle\bar{q}q\rangle=- {\rm i} \int\frac{{\rm d}^4k}{(2\pi)^4 } {\rm Tr}[S(k)]\;, \end{equation} $

(3) where "
$ {\rm Tr} $ " means the trace over Lorentz, color, and flavor matrices, and$S(k)=(\not k- M + {\rm i}\epsilon)^{-1}$ is the dressed-quark propagator (in Minkowski space) with${\rm i}\epsilon$ being the causality factor, introduced to exclude the singularity from the propagator.Substituting Eq. (3) into Eq. (2) and after performing the traces, we obtain
$ M=m+ 8 {\rm i} G_0 N_{f} N_{c} \int \frac{{\rm d}^{4}k}{(2\pi)^4}\frac{ M}{k^2 - M^2 + {\rm i}\epsilon}. $

(4) The gap equation Eq. (4) is based on the NJL Lagrangian. Eq. (1) describes the dynamical mass generation for
$ N_f $ and$ N_c $ ①.In this work, we are interested to include the anti-screening effects of the gluons and the screening effects of the light quarks; we extend the NJL model to an
$S U(N_c)$ gauge theory with an$ N_f $ number of light quarks. In this connection, we can determine the critical number of flavors or colors for the dynamical chiral symmetry breaking/restoration using an "NJL-type" model in the Schwinger-Dyson equations (SDE) framework. In the SDE scenario, the dynamical mass can be obtained from the dressed quark propagator:$ \begin{array}{*{20}{l}} S^{-1}(p)&=S^{-1}_{0}(p) + \Sigma(p)\,, \end{array} $

(5) where
$S_{0}(p)=(\not p- m + {\rm i}\epsilon)^{-1}$ is the bare quark propagator, and$ S(p) $ is the dressed quark propagator. The self energy$ \Sigma(p) $ is given by$ \Sigma(p)=-{\rm i}\int \frac{{\rm d}^4k}{(2\pi)^4} g^{2} D_{\mu\nu}(q)\frac{\lambda^a}{2}\gamma_\mu S(k) \frac{\lambda^a}{2}\Gamma_\nu(p,k)\,, $

(6) where
$ g^{2} $ is the QCD coupling constant, and$ \Gamma_\nu (k,p) $ is the dressed quark-gluon vertex. Here,$D_{\mu\nu}(q)= D(q) (-{\rm i} g_{\mu\nu} - \frac{q_{\mu} q_{\nu}}{q^2})$ is the gluon propagator in the Landau gauge, with$ g_{\mu \nu} $ being the metric tensor in the Minkowski space;$ q=k-p $ is the gluon four momentum, and$ D(q) $ is the gluon scalar function.$ \lambda^{a},s $ are the usual Gell-Mann's matrices. In the$S U(N_c)$ representation, the Gell-Mann's matrices satisfies the following identity:$ \sum^{8}_{a=1}\frac{{\lambda}^a}{2}\frac{{\lambda}^a}{2}=\frac{1}{2}\left(N_c - \frac{1}{N_c} \right)I, $

(7) where I is the unit matrix. We use the following form of the gluon propagator (in Landau gauge), in the infrared region where the gluons dynamically acquire a mass
$ \Lambda_{g}^{2} $ ($ \sim 500\pm 200 $ MeV) [48, 49] and bare vertex approximation ($ \Gamma_{\nu}(k,p)=\gamma^\nu $ ) (see for example [22, 50, 51]):$ g^2 D(q\rightarrow 0)=\frac{4\pi\alpha_{ir}}{\Lambda_{g}^{2}}=G, $

(8) which ensures the mapping of one-gluon exchange diagrams to a contact interaction in the NJL model. With a particular choice of the gap equation kernel, the dynamical quark mass function is merely a constant, and the dressed quark propagator takes the form [52]
$ S(k)=\frac{\not k+ M }{k^2- M^2 + {\rm i}\epsilon} . $

(9) The effective coupling G must exceed its critical value
$ G_c $ to describe dynamical chiral symmetry breaking. When G is greater than$ G_c $ , a nontrivial solution to the QCD gap equation bifurcates from the trivial one (see for example [53]). In this work, we use the effective coupling$ G=7.05\times 10^{-6} {\rm{MeV}}^{-2} $ ②, which can be obtained by setting the gluon mass scale$ \Lambda_{g}=587.9 $ MeV [41] and$ 4\pi\alpha_{ir}=2.44 $ . Substituting Eqs. (6)–(9) into Eq. (5) and taking the trace over the Dirac, colors, and flavors components, the gap equation is given by$ M = m + 8{\rm i} \mathcal{G}^{N_c}(N_f)\int{\frac{{\rm d}^{4}k}{(2\pi)^4}\frac{M}{k^2 - M^2 + {\rm i}\epsilon}}. $

(10) Thus, our truncation of the Schwinger-Dyson equations is equivalent to that of the NJL model in the Hartree mean field approximation, where
$ \mathcal{G}^{N_c}(N_f) $ is the effective coupling in which the color and flavor factors are incorporated as$ \mathcal{G}^{N_c}(N_f)=\left[\frac{1}{2}\left(N_c -\frac{1}{N_c}\right)\right]G(N_f). $

(11) To study the gap equation for the various number of flavors, we must modify the flavor sector
$ G(N_f) $ of the effective coupling$ \mathcal{G}^{N_c}(N_f) $ in a manner that it provides us the solution to the gap equation for the higher number of flavors. We shall use this modification as our modeling and it will aid us in determining$ N^{c}_{f} $ or$ N^{c}_{c} $ for chiral symmetry breaking or restoration. We adopt a similar method of modeling used by [5, 22] in which$ N^{c}_{f} $ are obtained from Schwinger-Dyson equations. According to [5, 22], the dynamically generated mass M should have the following type of relationship with$ N^{c}_{f} $ :$ M \backsim \sqrt{1 - \frac{N_f}{N^{c}_{f}}}, $

(12) where
$ N^{c}_{f} $ is the critical number of flavors. To obtain such a behavior in the four-fermion contact interaction NJL model, only a square root flavor-dependence in the coupling results in this observed behavior [22]. Therefore, to determine$ N^{c}_{f} $ , we modify the factor$ G(N_f) $ of Eq. (11) in similar fashion as in [22]:$ G(N_f) \longrightarrow \frac{9}{2}G\sqrt{1 - \frac{(N_{f}-2)}{\mathcal{N}_{f}^{c}}}, $

(13) where
$ \mathcal{N}_{f}^{c}=N^c_{f}+\eta $ is a guess value of the critical number of flavors. Our modification of the effective coupling is almost the same as in [22] but slightly different by a factor of$ 9/2 $ This is because the effective coupling model of [22] uses a local symmetry preserving four-point contact interaction, which, in the scalar-pseudoscalar channel, is Fierz equivalent to the term in NJL-Lagrangian Eq. (1) [42], (for Fierz transformation, see for example Appendix A in [41] and the Appendix at the end of this article).To obtain
$ N^{c}_{f} $ , we set$ \eta=2.3 $ which lies in the range as predicted in [22] by considering$ N^{c}_{f}=8 $ . Ref. [22] demonstrated that the parameter η appears because of the factor$ (N_f-2) $ in Eq. (13). For fixed$ N_c =3 $ and$ N_f =2 $ , our modified NJL effective coupling$ \mathcal{G}^{N_c}(N_f)\rightarrow GN_f N_c $ that normally used in NJL model gap equation Eq. (4).The four-momentum integral in Eq. (10) can be solved by splitting the four-momentum into time and space components. We denote the space part by a bold face letter
$ {k} $ and the time part by$ k_0 $ . Thus, Eq. (10) can be expressed as$\begin{aligned}[b] M =& m + 8{\rm i} \mathcal{G}^{N_c}(N_f) M\int_{0} ^{\infty}\frac{{\rm d}^3 {k}}{(2\pi)^4} \\&\times\int_{-\infty} ^{+\infty} {\frac{{\rm d} k_{0}}{ {k_{0}} ^{2} - E_{k} ^{2} + {\rm i}\epsilon}}. \end{aligned} $

(14) Here,
$ E_{k}=\sqrt{{| {k}}|^2 + M^2} $ , in which$ E_{k} $ denotes the energy per particle, and$ {k} $ is the$ 3 $ -momentum. On integrating over the time component of Eq. (14), we obtain the following expression:$ M = m + 8{\rm i} \mathcal{G}^{N_c}(N_f) M \int_{0} ^{\infty} \frac{{\rm d}^3 {k}}{(2\pi)^4} \frac{\pi}{{\rm i} E_{k}} $

(15) In spherical polar coordinates,
${\rm d}^3 {k} = {k}^2 {\rm d} {k} \sin\theta {\rm d}\theta {\rm d}\phi$ , and performing the angular integration, we obtain from Eq. (15)$ M = m + \frac{2 \mathcal{G}^{N_c}(N_f) M}{\pi^2} \int_{0} ^{\infty}{\rm d} {k} \frac{ {k}^2}{E_{k}}. $

(16) The integral occurring in Eq. (13) is a diverging integral, and we also know that the NJL model is not renormalizable owing to fermionic contact interaction. Different types of regularization schemes are used in the literature [40]. The regularization procedure we adopt in the present scenario is the three-dimensional (3d) momentum cut-off in which we remove the divergence by applying a certain high ultraviolet 3d-momentum cut-off Λ. Thus, Eq. (16) can be expressed as
$ M = m + \frac{2\mathcal{G}^{N_c}(N_f) M}{\pi^2} \int_{0} ^{\Lambda}{\rm d} {k} \frac{ {k}^2}{E_{k}}. $

(17) After integrating over the time component in Eq. (17), we obtain
$ M = m +\frac{\mathcal{G}^{N_c}(N_f) M}{\pi^2} \left[\Lambda\sqrt{{\Lambda}^2 + M^2} - M^2 {\rm arcsinh}\left(\frac{\Lambda}{M}\right)\right]. $

(18) In the present scenario, the quark-antiquark condensate, which serves as an order parameter for the chiral symmetry breaking, is defined as
$ -\langle \bar{q} q\rangle= \frac{M-m}{2\mathcal{G}^{N_c}(N_f)}. $

(19) The finite T and μ version of the NJL-model gap equation Eq. (10) can be obtained by adopting the standard convention for momentum integration i.e.,
$ \int\frac{{\rm d}^4k}{{\rm i}(2\pi)^4} f(k_0,{\bf{k}})\rightarrow T \sum\limits_{n} \int\frac{{\rm d}^3 k}{(2\pi)^3}f({\rm i}\omega_n+\mu,\bf{k}), $

(20) where
$ \omega_n = (2n+1)\pi T $ are the fermionic Matsubara frequencies. After performing some algebra, the gap equation Eq. (10) at finite T and μ can be expressed as$ M = m + 4\mathcal{G}^{N_c}(N_f)M\int^{\Lambda}_{0} \frac{{\rm d}^{3} {k}}{(2\pi)^{3}}\frac{1}{E_{k}} (1 - n_{\rm F}(T, \mu)- \bar{n}_{\rm F} (T, \mu)), $

(21) which is similar to Eq. (18) in a vacuum but modified by the thermo-chemical parts.
$n_{\rm F}(T, \mu)$ and$\bar{n}_{\rm F}(T, \mu)$ represent the Fermi occupation numbers for the quark and antiquark, respectively, and are defined as$\begin{aligned}[b]& n_{\rm F}(T, \mu) = \frac{1}{{\rm e}^{(E_{k}-\mu)/T} + 1} , \\& \bar{n}_{\rm F}(T, \mu)= \frac{1}{{\rm e}^{(E_{k}+\mu)/T} + 1}. \end{aligned}$

(22) On further simplifying, we obtain
$ \begin{aligned}[b] M =& m + \frac{\mathcal{G}^{N_c}(N_f) M}{\pi^2} \left[\Lambda\sqrt{{\Lambda}^2 + M^2} - M^2 {\rm arcsinh}\left(\frac{\Lambda}{M}\right)\right]\\&- \frac{\mathcal{G}^{N_c}(N_f)M}{\pi^{2}}\int_{0}^{\Lambda} {\rm d} {k} \frac{ {k}^2}{E_{k}} \left[ n_{\rm F}(T, \mu)+ \bar{n}_{\rm F} (T, \mu)\right]. \end{aligned} $

(23) If we set
$ \mu = T = 0 $ in Eq. (23), we obtain$n_{\rm F}=\bar{n}_{\rm F}=0$ ; thus, we can retain the gap equation in vacuum, i.e., Eq. (18). In the next section, we present a numerical solution of Eq. (18) for higher numbers of colors and flavors. -
In this section, we numerically solve the gap equation Eq. (18) with a particular choice of the parameters, i.e., the cutoff parameter
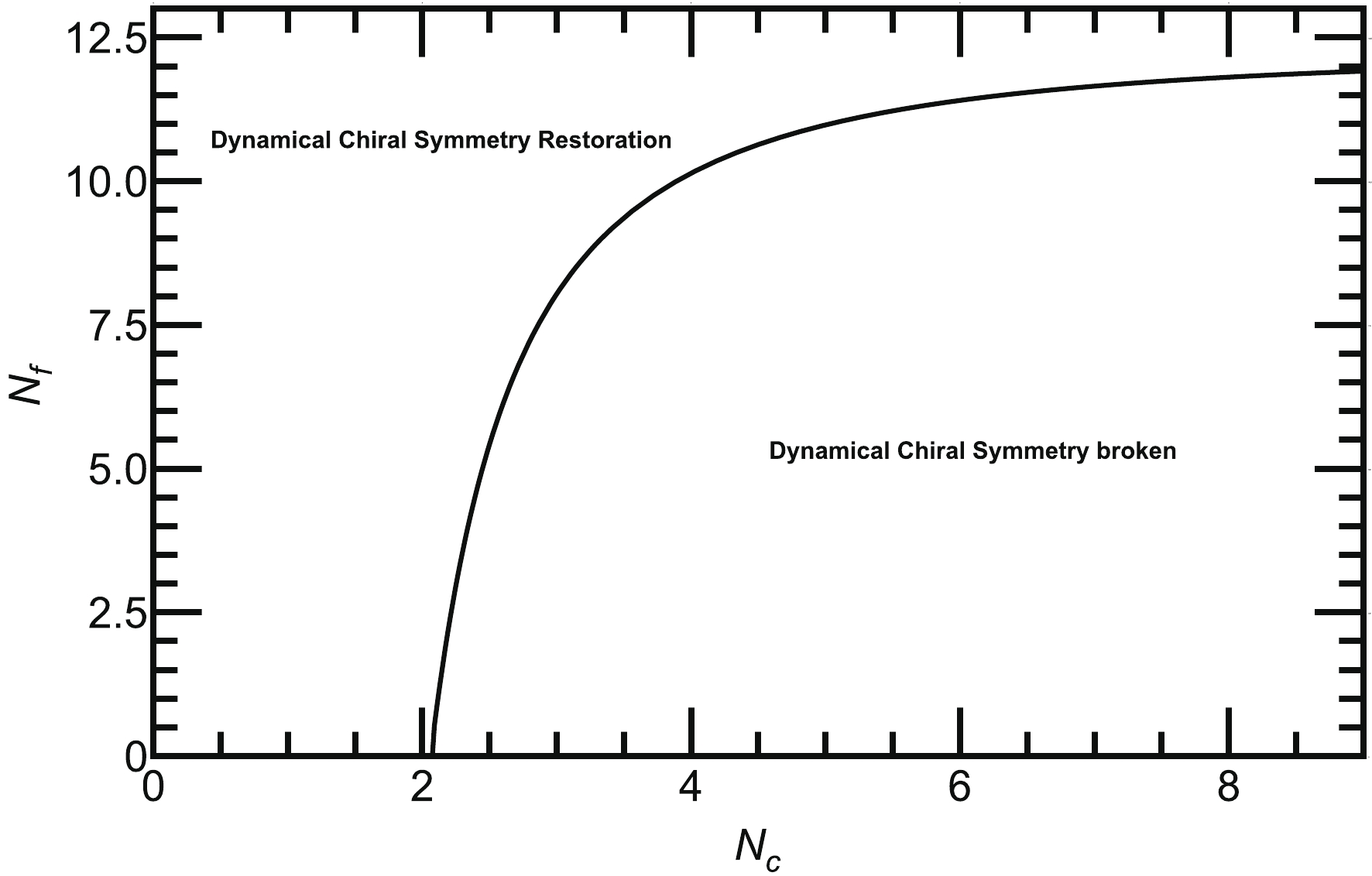
$ \Lambda = 587.9 $ MeV③,$G=7.05\times 10^{-6}$ MeV$ ^{-2} $ , and$ m = 5.6 $ MeV, which have been determined to reproduce the pion decay constant$ f_{\pi} = 92.4 $ MeV and pion mass$ m_{\pi} = 135.0 $ MeV in the two-flavors NJL model [41]. The solution of our gap equation with modified color-flavor dependence effective coupling Eq. (11) for two light flavors$ N_f = 2 $ (i.e., up and down) and for$ Nc = 3 $ yields the dynamical mass$ M = 399 $ MeV. From Eq. (19), we calculate the corresponding quark-antiquark condensate as$ -\langle \bar{q} q\rangle^{1/3}=250 $ MeV. In this scenario, our results are consistent with that obtained in [41]. Next, we solve the gap equation Eq. (18), for various$ N_c $ and$ N_f $ . Initially, we solve the gap equation for fixed$ N_f = 2 $ but varying$ N_c $ and plot the dynamically generated quark mass in Fig. 1(a) as a function of$ N_c $ . We observe that the chiral symmetry is dynamically broken when$ N_c $ exceeds a critical value,$ N_c=N^{c}_{c} $ , and remains broken for larger values of$ N_c $ . The corresponding quark-antiquark condensate$ -\langle \bar{q} q\rangle^{1/3} $ is shown in Fig. 1(b).$ N^{c}_c $ is obtained from the peak of the color gradient of the quark-antiquark condensate$ -\partial_{N_c}\langle \bar{q} q\rangle^{1/3} $ and is depicted in Fig. 1(c), from which we observe that the chiral symmetry is dynamically broken above$ N^{c}_{c}\approx2.2 $ nd is thus consistent with the predicted value obtained in [22]. Next, we fix$ N_c=3 $ and solve Eq. (18) for various$ N_f $ as shown in Fig. 2(a). The plot demonstrates that the dynamically generated mass monotonically decreases with the increase in$ N_f $ until it reaches a critical value$ N^{c}_{f} $ , where the dynamical mass vanishes and only bare quark mass survives; thus, chiral symmetry is dynamically restored when$ N_f $ exceeds$ N^{c}_f $ . In Fig. 2(b), we plot$ -\langle \bar{q} q\rangle^{1/3} $ as a function of$ N_f $ , and its flavor gradient$ -\partial_{N_f}\langle \bar{q} q\rangle^{1/3} $ is depicted in Fig. 2(c). Thus, we obtain$ N^{c}_{f}\approx8 $ from the peak of the flavor gradient$ -\partial_{N_f}\langle \bar{q} q\rangle^{1/3} $ . Our results in this scenario agree with that obtained in [22]. In Fig. 3, we plot the critical line between$ N_{f} $ and$ N_{c} $ in the$ N_c-N_f $ plane; both the parameters opposes the effect of each other. Fig. 3 clearly demonstrates that the$ N^{c}_{f} $ required for dynamical chiral symmetry restoration increases as$ N_c $ increases, and as$ N_{f} $ increases, the$ N^{c}_{c} $ required for the dynamical chiral symmetry breaking increases. For better understanding, we have tabulated some data for the variation in$ N^{c}_{f} $ with various$ N^{c}_{c} $ in Table 1. In the next section, we discuss the dynamical chiral symmetry breaking and its restoration with$ N_c $ and$ N_f $ at finite T.
Figure 1. (color online) (a) Behaviors of dynamical qurak mass as a function of number of colors
$ N_c $ for two fixed flavors$ N_f=2 $ . (b) Quark-antiquark condensate as a function of$ N_c $ . (c) Color gradient of the quark-antiquark condensate; the peak of the gradient is at$ N_c\approx 2.2 $ , which is the critical number for dynamical chiral symmetry breaking.$ N_{c} $ 

2.2 3 4 5 6 7 8 9 10 $ N_{f} $ 

3 8 9.5 10.3 10.7 11 11.2 11.3 11.4 Table 1. Data for plotting the critical line in the
$ N_c-N_f $ plane as depicted in Fig. 3.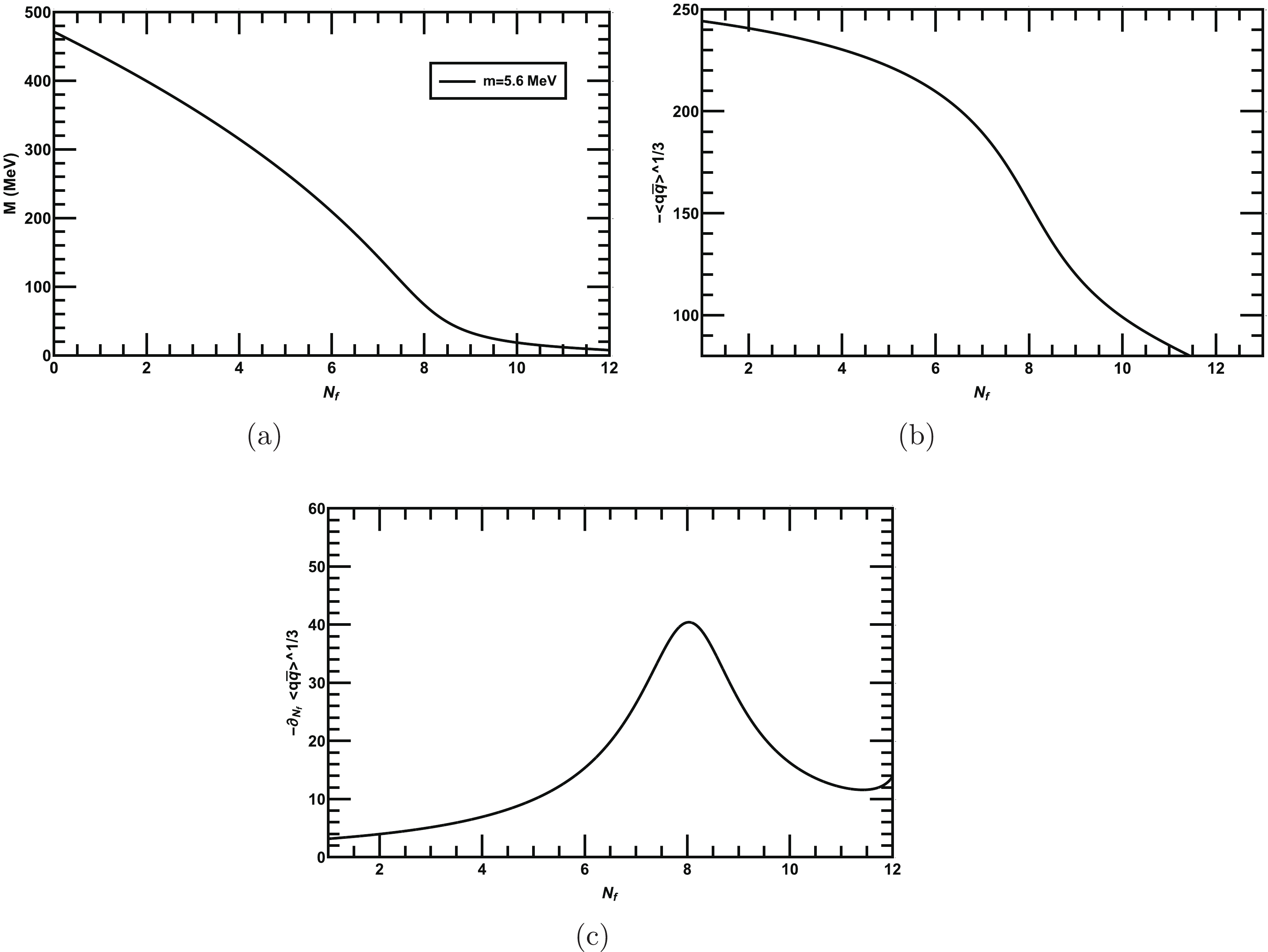
Figure 2. (a) Behavior of the dynamical mass as a function of various
$ N_f $ for fixed$ N_c=3 $ . The dynamical mass monotonically decreases with increasing$ N_f $ . (b) Quark-antiquark condensate as a function of$ N_f $ . (c) Flavor gradient of the quark-antiquark condensate as a function of$ N_f $ . The peak of the gradient is at$ N_{f}\approx8 $ , which is the critical number of flavors$ N^{c}_{f} $ , above which the dynamical chiral symmetry is restored. -
In this section, we numerically solve the gap equation Eq. (23) to understand dynamical symmetry breaking and restoration for various
$ Nc $ and$ N_f $ and at finite T. Initially, we fix$ N_f=2 $ and plot the dynamical mass in Fig. 4(a) as a function of$ N_c $ for various T. The corresponding condensate is depicted in Fig. 4(b). We observe that as T increases, the dynamical symmetry is broken above$ N^{c}_c $ . We determine the$ N^{c}_{c} $ for various values of T from the peaks of the color gradient$ -\partial_{N_c}\langle \bar{q} q\rangle^{1/3} $ , as shown in Fig. 4(c). The peaks of the gradient shift towards larger values of$ N_c $ as we increase T. Hence,$ N_c $ tends to enhance the dynamical quark mass and condensate while T suppresses both, and as a result, we require higher values of$ N_c $ for dynamical chiral symmetry breaking. Thus,$ N^{c}_{c} $ increases with T, as shown in the phase diagram drawn in the$ N_c-T $ plane in Fig. 4(d). This means that in the presence of a heat bath, a large$ N^{c}_{c} $ is required for dynamical chiral symmetry breaking. The nature of the transition at each temperature$ T=T_c $ is of crossover.
Figure 4. (color online) (a) Behavior of dynamical mass as a function of
$ N_c $ for fixed$ N_f = 2 $ and for various T. (a) Quark-antiquark condensate as a function of$ N_c $ for various T and fixed$ N_f = 2 $ . (c) Color gradient of quark-antiquark condensate for various T. The peaks of the gradient shifts towards their larger values of$ N_{c} $ as T increases. (d) Phase diagram for dynamical chiral symmetry breaking/restoration in the$ N_{c}-T $ plane. The higher the T, the larger value of$ N_{c} $ required for the dynamical symmetry breaking.Now, for fixed
$ N_c = 3 $ , we plot the dynamical mass as a function of$ N_f $ for different values of T as shown in Fig. 5(a), and the corresponding condensate is depicted in Fig. 5(b). In this case, we observe that the dynamical mass as a function of$ N_f $ is suppressed as T increases. We obtain the critical number of flavors$ N^{c}_f $ for different T from the peaks of the flavor gradient$ -\partial_{N_f}\langle \bar{q} q\rangle^{1/3} $ , as shown in Fig. 5(c). We observe that the peaks shifted towards their smaller$ N_f $ values. Thus,$ N^{c}_{f} $ monotonically decreases as T increases, as demonstrated in the phase diagram in the$ N_f-T $ plane in Fig. 5(d). Therefore, in the presence of a heat bath, a lower$ N^{c}_{f} $ is required for dynamical chiral symmetry breaking/restoration. The nature of the transition at each temperature T is of crossover. In the next section, we investigate the behavior of chiral symmetry breaking and restoration at a finite chemical potential μ, for various$ N_c $ and$ N_f $ .
Figure 5. (color online) (a) Behavior of dynamical mass as a function of
$ N_f $ for fixed$ N_c=3 $ and various T. As T increases, the dynamical mass is suppressed. (b) Behavior of the quark-antiquark condensate as a function of$ N_f $ for various T. (c) Flavor gradient of the condensate for various T, which shows that as T increases, the peaks shift towards their lower$ N_{f} $ values. (d) Phase diagram for the dynamical chiral symmetry breaking/restoration in the$ N_{f}-T $ plane. -
In this section, we discuss dynamical chiral symmetry breaking and its restoration at a finite μ for various
$ N_c $ and$ N_f $ . The dynamical mass as a function of μ for fixed$ N_f=2 $ and various$ N_c $ is shown in Fig. 6(a). We observe that the chiral symmetry is dynamically restored when μ exceeds a critical value$ \mu_c $ . The discontinuity in the dynamical mass at$ \mu=\mu_{c} $ shows that the nature of the phase transition is of first-order, while the smooth decrease in the dynamical mass represents the crossover transition. This means that μ suppresses the dynamical mass and condensate in contrast to$ N_c $ , which strengthens it. We can determine the critical number of colors$ N^{c}_{c} $ from the peak of$ -\partial_{N_c}\langle \bar{q} q\rangle^{1/3}_{\mu} $ for various μ. We plot the phase diagram in the$ N_c-\mu $ plane, where we show the variation in$ N^{c}_{c} $ with μ in Fig. 6(b). This plot shows that as we increase μ,$ N^{c}_{c} $ also increases. For example, at$ \mu = 100 $ MeV, we require a lower critical number of colors (i.e,$ N^{c}_c= 2.2 $ ) for chiral symmetry breaking compared with$ \mu = 250 $ MeV (i.e.,$ N^{c}_c= 2.5 $ ). We observe the crossover phase transition for$ N_c \leq 2.5 $ and first-order transition for$ N_c > 2.5 $ differentiated by a critical endpoint$ (N_{c}^{c}\approx2.5,\; \mu^{c}_c\approx290 $ MeV). Next, we fix$ N_c=3 $ and plot the dynamical mass as a function of μ for various$ N_f $ in Fig. 7(a). Dynamical chiral symmetry is restored when the chemical potential reaches a critical value$ \mu_c $ for different$ N_f $ . However, the nature of phase transition is of first-order for$ N_f\leq5 $ and crossover for$ N_f\geq5 $ . The dynamical mass as a function of μ is suppressed with the increase in$ N_f $ . We then determine the critical number of flavors$ N^{c}_f $ for each chemical potential μ from the peak of$ -\partial_{N_c}\langle \bar{q} q\rangle^{1/3}_{\mu} $ and plot the variation in$ N^{c}_{f} $ versus$ \mu_c $ in the$ N_f-\mu $ plane, as depicted inFig. 7(a). We note that$ N^{c}_{f} $ decreases with the increase in μ. The nature of the phase transition is crossover until the critical endpoint$ (N_{c}^{f}=5, \mu^{f}_c=290 $ MeV) where at and above it, the nature of transition changes to first-order.
Figure 6. (color online) (a) Dynamical quark mass as a function of μ for various
$ N_c $ and fixed$ N_f=2 $ . The plot shows that the dynamical mass decreases as we increase μ. The discontinuity in the mass function for$ N_c\geq2.5 $ demonstrates that the nature of the phase transition is of first-order, while that of$ N_c<2.5 $ is crossover. (b) Phase diagram for dynamical chiral symmetry breaking/restoration in the$ N_c-\mu $ plane. The nature of the phase transition is of smooth crossover until the critical endpoint$ (N_{c}^{c}\approx2.5, \mu^{c}_c\approx 290 $ MeV), while above it, the transition changes to the first-order.
Figure 7. (color online) (a) Behavior of the dynamical quark mass as a function of μ at various
$ N_f $ and fixed$ N_c=3 $ . The plot demonstrates that the dynamical chiral symmetry is restored above a critical$ \mu_c $ for each$ N_c $ . (b) Phase diagram for dynamical chiral symmetry breaking/restoration in the$ N_f-\mu $ plane. The nature of the phase transition is smooth crossover for$ N_f< 5 $ and changes to first-order for$ N_f\geq5 $ . Both transitions are differentiated by a critical endpoint$ (N_{c}^{f}\approx5,\; \mu^{f}_c \approx 290 $ MeV).The overall results shows that at higher values of μ, we require a higher
$ N^{c}_{c} $ and lower$ N^{c}_{f} $ for dynamical chiral symmetry breaking/restoration. In the next section, we investigate the simultaneous effects of T and μ on chiral phase transition for various$ N_c $ and$ N_f $ . -
In this section, we sketch the QCD phase diagrams in the
$ T-\mu $ plane for various$ N_c $ and$ N_f $ . First, the QCD phase diagram is shown in Fig. 8 for fixed$ N=2 $ and for various number of colors (i.e,$ N_c = 3, 4, 5, 6 $ ) at T and μ. We obtain the critical temperature$ T_c $ and critical chemical potential$ \mu_c $ from the peaks of the thermal and chemical potential gradients of the quark-antiquark condensate, receptively. Initially, we plot the phase diagram for$ N_f = 2 $ and$ N_c = 3 $ , which shows that at finite T but at$ \mu= 0 $ , the dynamical chiral symmetry is broken for$ T\leq T_c \approx 235 $ MeV, while above that, it is restored. The phase transition is a crossover in this case. At finite μ and$ T = 0 $ , the dynamical symmetry is observed to be broken below$ \mu_c \approx 380 $ MeV, while above that, it is restored via first-order phase transition. We confirm from Fig. 8 that the crossover line in the phase diagram starts from a finite T-axis (for$ \mu=0 $ ) never ends up at finite μ-axis (for$ T=0 $ ); hence, a critical endpoint exists at which the crossover transition changes to first-order transition. We determine the co-ordinates of the critical endpoint at$ (\mu^{E}_{c}\approx 330, T^{E}_{c}\approx 81) $ MeV. Our analysis for$ N_f = 2 $ and$ N_c = 3 $ , with a particular choice of parameters of NJL-type model, which is based on the SDE truncation, is consistent with that of the NJL model QCD phase diagram sketched in [41]. Subsequently, we extend it to various$ N_c $ . The solid-triangular lines represents the crossover phase transition for various$ N_c $ phase diagrams, and the dotted dashed lines for the first-order phase transition is separated by the big red dots (the critical endpoints) in all the phase diagrams. We observe that$ T_c $ ,$ \mu_c $ , and co-ordinates of the critical endpoints ($ \mu^{E}_c $ ,$ T^{E}_c $ ) are shifted towards their higher values as$ N_c $ increases. The variation in$ T_c $ ,$ \mu_c $ , and ($ \mu^{E}_c $ ,$ T^{E}_c $ ) with$ N_c $ are tabulated in Table 2. This means that as$ N_c $ increases, the strength of the non-abelian interaction increases. A higher$ N_c $ provides stronger bindings between the quarks. To undo that effect, we require a higher T or μ for the dynamical chiral symmetry breaking/restoration, as Fig. 8 confirms. Refs. [54, 55] demonstrated that$ \mu_c $ increases with$ N_c $ as$ \mu_c\sim\sqrt{N_c} $ . Additionally, effective lattice simulations with heavy quarks have indicated the same observation about the shifting of critical endpoint in the phase diagram for higher$ N_c $ [56, 57]. Ref. [58] argued that$ T_c $ increases with$ N_c $ as$ T_c\sim\sqrt{N_c} $ . However, a lattice simulation of$S U(N_c)$ in the quenched approximation, based on the string tension σ, predicted an opposite behavior, i.e.,$ T_c (\mu=0)/\sqrt{\sigma} $ decreases as$ N_c $ increases, and the transition is first-order at$ T_c $ [59], for more clear demonstration, see for example [60]④, whereas, in the real-world for$ N_c = 3 $ and$ N_f=2 $ , the QCD exhibits a crossover transition near$ T_c $ [61].S.No $ N_c $ 

$ T_c $ /MeV at

$ \mu=0 $ 

$ \mu_c $ /MeV at

$ T=0 $ 

$(\mu^{E}_{c}, T^{E}_{c}) /{\rm{MeV} }$ 

01 3 235 380 (330, 81) 02 4 377 450 (415,185) 03 5 503 510 (509,271) 04 6 623 609 (604,350) Table 2. Data for the variation in
$ T_c $ and ($ \mu^{E}_{c}, T^{E}_{c} $ ) in the phase diagrams with various$ N_c $ , for fixed$ N_f = 2 $ and$ m=5.6 $ MeV.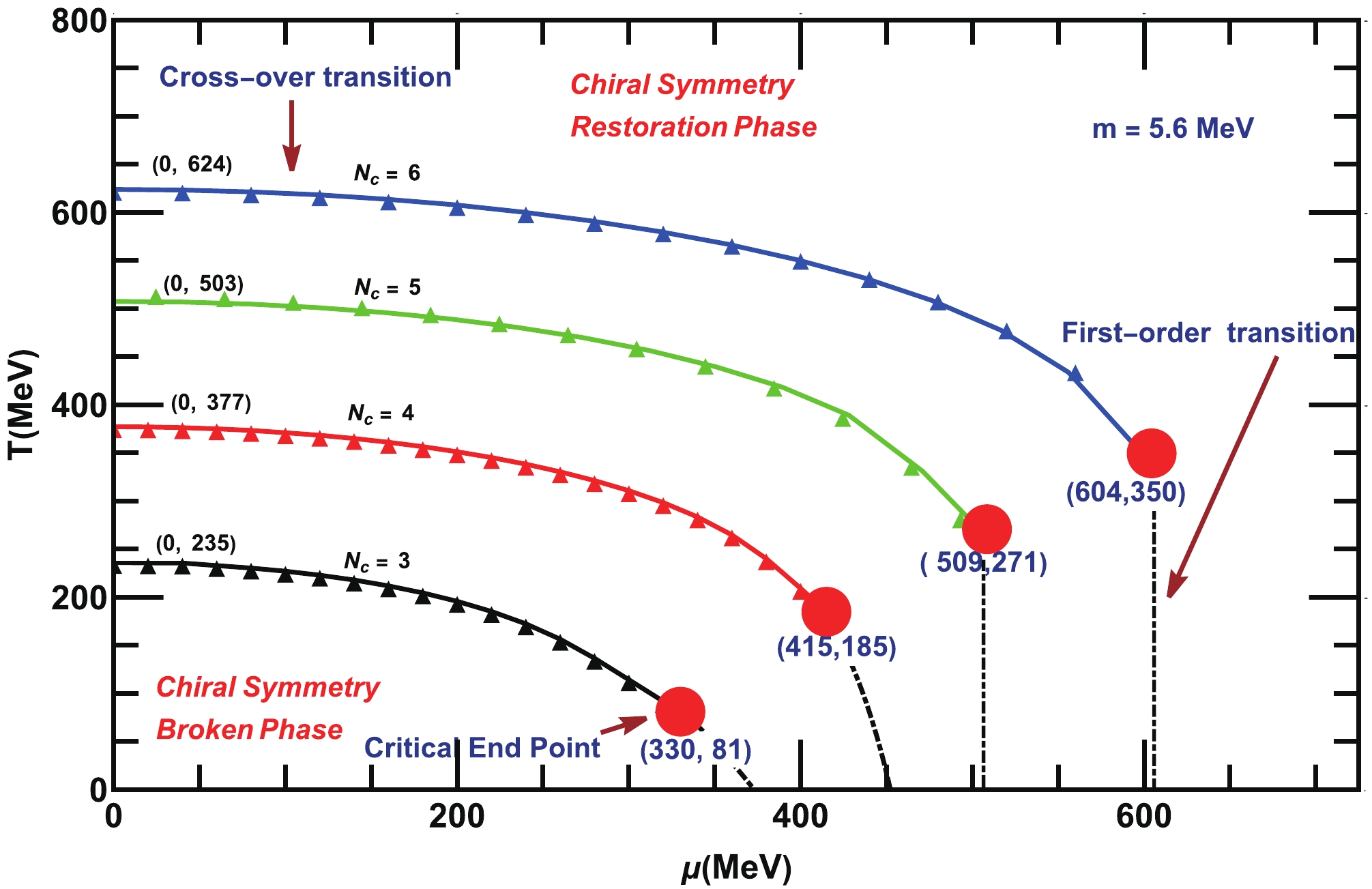
Figure 8. (color online) QCD phase diagram in the
$ T-\mu $ plane for various number of colors$ (N_c =3,4, 5,6) $ and for fixed flavor$ N_f = 2 $ . The all solid-triangle lines represent the crossover phase transitions, and the dot-dashed lines represent the first-order phase transitions. The big red-dots for the critical endpoints in each phase diagrams.Next, we draw the QCD phase diagrams in Fig. 9 for fixed
$ N_c = 3 $ but various numbers of light quark flavors (i.e.,$ N_f = 2,3, 4, 5 $ ). We use the same technique and same parameters to create the phase diagrams, but now we fix$ N_c = 3 $ and vary$ N_f $ . All the phase diagrams in Fig. 9 indicate their regular behaviors but are suppressed with increasing$ N_f $ . We note that as$ N_f $ varies,$ T_c $ , the$ \mu_c $ potential, and the coordinates of the critical endpoints ($ \mu^{E}_c $ ,$ T^{E}_c $ ) are suppressed with the increase in$ N_f $ . In Table 3, we tabulate the variation in$ T_c $ ,$ \mu_c $ , and ($ \mu^{E}_c $ ,$ T^{E}_c $ ) with a large$ N_f $ .S.No $ N_f $ 

$ T_c $ /MeV at

$ \mu=0 $ 

$ \mu_c $ /MeV at

$ T=0 $ 

CEP $(\mu^{E}_{c}, T^{E}_{c})/{\rm{ MeV} }$ 

01 2 235 380 (330, 81) 02 3 216 355 (320, 64) 03 4 194 330 (308, 40) 04 5 169 300 (280, 25) Table 3. Data for the variation in
$ T_c $ and ($ \mu^{E}_{c}, T^{E}_{c} $ ) in the phase diagrams with various$ N_f=2 $ , for fixed$ N_c = 3 $ and$ m=5.6 $ MeV.
Figure 9. (color online) QCD phase diagram for the
$ T_c -\mu_c $ plane for various number of flavors$ (N_c = 2,3,4,5) $ , for fixed$ N_c = 3 $ . All solid-triangle lines represent the crossover phase transitions and dot-dashed lines the first-order phase transition. The big red-dots represent the location of the critical endpoint in each phase diagram.In the next section, we summarize our findings and draw the conclusions.
-
In this work, we have studied the dynamical chiral symmetry breaking/restoration for light quark flavors
$ N_f $ and colors$ N_c $ . Additionally, we investigate the impact of$ N_c $ and$ N_f $ on the QCD phase diagram at finite temperature T and quark chemical potential μ. For this purpose, we use the NJL-type model dressed with the color-flavor dependence of effective coupling$ \mathcal{G}^{N_c}(N_f) $ in the Schwinger-Dyson equations framework, which has advantages to study the QCD gap equation for$ N_f=0 $ as well as a higher number of flavors$ N_f $ . Our observations show that for fixed$ N_c=3 $ and increasing$ N_f $ , the dynamical chiral symmetry is partially restored when$ N_f $ exceeds a critical value$ N_{f}^{c}\approx 8 $ . Our results have a remarkable resemblance with the modern lattice QCD simulation and Schwinger-Dyson's equation predictions. For$ N_f=2 $ , as$ N_c $ increases, we determine the critical number of colors as$ N_{c}^{c}\approx 2.2 $ , above which the dynamical chiral symmetry is broken. The dramatic opposed effects between the two parameters$ N_{f}^{c} $ and$ N_{c}^{c} $ have been observed. This corresponds with our expectation and conforms to previous studies [22], that is, increasing$ N_f $ suppresses the dynamical generated quark mass and quark-antiquark condensate, whereas increasing$ N_c $ enhances the dynamical mass and condensate. At finite T, our results show that the dynamical chiral symmetry is restored when T reaches a critical value$ T_c $ . A higher T suppresses the dynamical quark mass and condensate in contrast to a higher$ N_c $ ; consequently, the larger$ N_c $ is required for chiral symmetry breaking. Thus, the critical value$ N^{c}_c $ (for$ N_f = 2 $ ) increases as T increases. Our results at finite T, for fixed$ N_c=3 $ and varying$ N_f $ shows that the dynamical quark mass and condensate monotonically decreases as$ N_f $ increases; hence, fewer$ N^{c}_f $ are required to restore the dynamical chiral symmetry at finite T. As a result,$ N^{c}_{f} $ decreases as T increases. The nature of the phase transition remains a crossover throughout for both phase diagrams drawn in the$ N_{c}- T_c $ and$ N_{f}-T_c $ planes. Similarly, in the presence of quark chemical potential μ, we conclude that the$ N_{c}^{c} $ for the dynamical chiral symmetry restoration is enhanced as μ increases and vice versa. The nature of the phase transition in this case is observed to be smooth crossover until the critical endpoint$ (N^{cp}_{c}\approx2.5 $ ,$ \mu^{cp}_c\approx 290 $ MeV), and above that, the transition changes to the first-order. We further observe that the$ N^{c}_f $ required for the dynamical symmetry restoration is suppressed as μ increases. In this case, the nature of the phase transition is smooth crossover until the critical endpoint$ (N^{cp}_{f}\approx 5,\mu^{cp}_{f}\approx290 $ MeV) and above that, the transition changes to the first-order.Finally, we have sketched the QCD phase diagram in the
$ T-\mu $ plane for various$ N_c $ and$ N_f $ . We observe that$ T_c $ ,$ \mu_c $ , and the location of critical endpoint ($ \mu^{E}_c $ ,$ T^{E}_c $ ) shift toward higher values with increasing$ N_c $ . For increasing$ N_f $ , the scenario is reversed, i.e.,$ T_c $ ,$ \mu_c $ , and ($ \mu^{E}_c $ ,$ T^{E}_c $ ) shift towards their lower values with the increasing$ N_f $ . We conclude that considering the number of light quark flavors (or colors) yields an important impact on the QCD phase diagram in addition to the heat bath and background fields. This work not only connects the color-flavor dependence with T and μ in congruence with the existing theoretical and phenomenological interpretations, but also has important consequences related to the heavy-ion collision experiments. In the future, we plan to investigate the color-flavor phase diagram in the presence of background fields and other light hadrons properties. -
We thank A. Bashir and A. Raya for their valuable suggestions and guidance during the completion of this manuscript. We acknowledge the organizers and participants of the "19th International Conference on Hadron Spectroscopy and Structure in memoriam Simon Eidelman (HADRON-2021), Mexico (online)" and "International Union of on Pure and Applied Physics (IUPAP-2022) Pakistan (online)", for providing a conducive environment for the exchange of ideas during the presentation of this work, which led to the genesis of this manuscript. We also thank the colleagues of Institute of Physics, Gomal University, for their encouragement.
-
Fierz Transformation is a re-arrangement of fermion operator products in the Dirac, flavor, and color space using index-exchanging properties of the gamma and
$S U(N_c)$ generator matrices. Consider an NJL-type interaction (for detail, see Appendix A in [41]):$ \begin{array}{*{20}{l}} {\cal L}_{\rm int}=g_{I}(\bar{q}\hat{\Gamma}^{I}q)^{2}=g_{I}\Gamma^{I}_{ij}\Gamma^{I}_{kl}\bar{q}_i q_j \bar{q}_k q_l, \end{array} \tag{A1}$

where the operator
$ \hat{\Gamma}^{I} $ corresponds to the quark-antiquark channel I. Considering the anticommutation relation for fermions, we have the following identities$ \begin{aligned}[b]& {\cal L}_{\rm exc}=-g_{I}\Gamma^{I}_{ij}\Gamma^{I}_{kl}\bar{q}_i q_l \bar{q}_k q_j\ \ {\rm and } \\& {\cal L}_{qq}=g_{I}\Gamma^{I}_{ij}\Gamma^{I}_{kl}\bar{q}_i\bar{q}_k q_l q_j. \end{aligned}\tag{A2} $

In the Hartree-type approximation, we can rewrite the operators
$ \Gamma^{I}_{ij}\Gamma^{I}_{kl}=\sum\limits_{M}c^{I}_{M}\Gamma^{I}_{ij}\Gamma^{I}_{kl}, \tag{A3} $

to obtain
$ {\cal L}_{\rm exc}=-g_{I}\sum\limits_{M}c^{I}_{M} (\bar{q}\hat{\Gamma}^{I}q)^{2}. \tag{A4} $

To describe the combined effect of direct plus exchange interaction by Lagrangian, we can perform a Fierz transformation in the quark-antiquark channel:
${\cal L}_{q\bar{q}}={\cal L}_{\rm dir} (\equiv {\cal L}_{\rm int})+ {\cal L}_{\rm exc} =\sum\limits_{M}G_{M}(\bar{q}\hat{\Gamma}^{I}q)^{2}, \tag{A5}$

where
$ G_M $ represents the effective coupling constants and sum runs over all quark-antiquark channels M.$ G_M $ can be obtained from the$ g_I $ i.e,$ G_M=c^{I}_{M} g_I $ for$ M\neq I $ and$ G_M=(1-c^{I}_{I}) g_I $ .In the same manner, we can employ a Fierz transformation into the quark-quark channel to write the an effective quark-quark interaction as
$ {\cal L}_{q q}=\sum\limits_{D}H_{D}(\bar{q}\hat{\Gamma}^{D} C \bar{q}^{T})(q^{T}C \hat{\Gamma}^{D}q),\tag{A6} $

where D corresponds to the various diquark channels.
$ H_D=d^{I}_{D} g_I $ are the quark-quark effective coupling constants. The coefficients$ c^{I}_{M} $ and$ d^{I}_{D} $ of the operators are discussed in detail in Appendix A.2 of [41]. Thus, if we know the Lagrangian${\cal L}_{\rm int}$ ,$ G_M $ and$ H_D $ are uniquely fixed. To avoid double counting,$ {\cal L}_{\bar{q} q} $ and$ {\cal L}_{q q} $ are to be used in Hartree approximation only.A simple Fierz transformation of the color-current–color-current interaction (which can be obtained from the QCD Lagrangian by converting the original
$S U(N_c)$ gauge symmetry into a global symmetry of the quark color-currents) is given by$ \begin{array}{*{20}{l}} {\cal L}_{\rm int}=-g(\bar{q}\gamma^{\mu}\lambda^{\alpha} q)^{2}. \end{array}\tag{A7} $

The quark-antiquark interaction can be expressed as
$ \begin{aligned}[b] {\cal L}_{\bar{q}q}=&\frac{2(N^{2}_c-1)g}{N_fN^{2}_c} \Bigg[(\bar{q}q)^2+(\bar{q} {\rm i}\gamma_5 q)^2- \frac{1}{2}(\bar{q}\gamma^{\mu}q)^2-\frac{1}{2}(\bar{q}\gamma^{\mu}\gamma_5 q)^2\Bigg]\\&+\frac{(N^{2}_c-1)g}{N^{2}_c}\Bigg[(\bar{q}\tau_{a} q)^2+(\bar{q} {\rm i}\gamma_5 \tau_{a}q)^2- \frac{1}{2}(\bar{q}\gamma^{\mu}\tau_{a}q)^2\\&-\frac{1}{2}(\bar{q}\gamma^{\mu}\gamma_5\tau_{a} q)^2\Bigg]-+\frac{g}{N_c N_f} \Bigg[(\bar{q}\lambda_{a} q)^2+(\bar{q} {\rm i}\gamma_5 \lambda_{a}q)^2\\&- \frac{1}{2}(\bar{q}\gamma^{\mu}\lambda_{a}q)^2-\frac{1}{2}(\bar{q}\gamma^{\mu}\gamma_5\lambda_{a} q)^2\Bigg]- \frac{g}{2N_c} \Bigg[(\bar{q}\tau_{a}\lambda_{a^{\prime}} q)^2\\&+(\bar{q}\tau_{a} {\rm i}\gamma_5 \lambda_{a^{\prime}}q)^2- \frac{1}{2}(\bar{q}\gamma^{\mu}\tau_{a}\lambda_{a^{\prime}}q)^2-\frac{1}{2}(\bar{q}\gamma^{\mu}\gamma_5 \tau_{a}\lambda_{a^{\prime}} q)^2\Bigg]\\=&\frac{(N^{2}_c-1)g}{N^{2}_c} \sum^{N^{2}_{f}-1}_{a=0}\Bigg[(\bar{q}\tau_{a} q)^2+(\bar{q} {\rm i}\gamma_5 \tau_{a}q)^2- \frac{1}{2}(\bar{q}\gamma^{\mu}\tau_{a}q)^2\\&-\frac{1}{2}(\bar{q}\gamma^{\mu}\gamma_5\tau_{a} q)^2\Bigg]- \frac{g}{2N_c}\sum^{N^{2}_{f}-1}_{a=0} \Bigg[(\bar{q}\tau_{a}\lambda_{a^{\prime}} q)^2+(\bar{q}\tau_{a} {\rm i}\gamma_5 \lambda_{a^{\prime}}q)^2\\&- \frac{1}{2}(\bar{q}\gamma^{\mu}\tau_{a}\lambda_{a^{\prime}}q)^2-\frac{1}{2}(\bar{q}\gamma^{\mu}\gamma_5 \tau_{a}\lambda_{a^{\prime}} q)^2\Bigg], \end{aligned} \tag{A8}$

where
$ \tau_a $ denotes operators in the$S U(N_f)$ flavor space, and$ \lambda_a $ are the operators in the$S U(N_c)$ color space. The flavor and color indices run from$ 1 $ to$ N^{2}_{f,c}-1 $ . Comparing the coefficient of the scalar$ (\bar{q}q))^2 $ and pseudo-scalar$(\bar{q} {\rm i}\gamma_5 \tau_{a}q)^2$ terms from Eqs. (1) and (31), we obtain$ G:= {\rm coeff.}\; (\bar{q}q)^2= \frac{2(N^{2}_c-1)g}{N_fN^{2}_c}. \tag{A9}$

$ G:= {\rm coeff.}\; (\bar{q}{\rm i}\gamma_5 \tau_{a} q)^2 = \frac{(N^{2}_c-1)g}{N^{2}_c}. \tag{A10}$

For
$ N_c=3 $ and$ N_f=2 $ , we obtain$ G=\dfrac{8}{9} g $ .Now, for the quark-quark interaction, we obtain
$ \begin{aligned}[b] {\cal L}_{qq}=&\frac{(N^{2}_c+1)g}{2N_c} [ (\bar{q}{\rm i}\gamma_5 C\tau_{A} \lambda_{A^{\prime}}\bar{q}^{T})(q^{T}C i\gamma_5 C\tau_{A} \lambda_{A^{\prime}} q)\\&+(\bar{q} C\tau_{A} \lambda_{A^{\prime}}\bar{q}^{T})(q^{T} C\tau_{A} \lambda_{A^{\prime}} q)\\& -\frac{1}{2} (\bar{q}\gamma^\mu \gamma_5 C\tau_{A} \lambda_{A^{\prime}}\bar{q}^{T})(q^{T}C \gamma_\mu\gamma_5 C\tau_{A} \lambda_{A^{\prime}} q)\\&-\frac{1}{2}(\bar{q}\gamma^\mu C\tau_{A} \lambda_{A^{\prime}}\bar{q}^{T})(q^{T}\gamma_\mu C\tau_{A} \lambda_{A^{\prime}} q)]\\&-\frac{(N^{2}_c-1)g}{2N_c}[ (\bar{q}{\rm i}\gamma_5 C\tau_{S} \lambda_{S^{\prime}}\bar{q}^{T})(q^{T}C {\rm i}\gamma_5 C\tau_{S} \lambda_{S^{\prime}} q)\\&+(\bar{q} C\tau_{S} \lambda_{S^{\prime}}\bar{q}^{T})(q^{T} C\tau_{S} \lambda_{S^{\prime}} q)\\& -\frac{1}{2} (\bar{q}\gamma^\mu \gamma_5 C\tau_{S} \lambda_{S^{\prime}}\bar{q}^{T})(q^{T}C \gamma_\mu\gamma_5 C\tau_{S} \lambda_{S^{\prime}} q)\\&-\frac{1}{2}(\bar{q}\gamma^\mu C\tau_{S} \lambda_{S^{\prime}}\bar{q}^{T})(q^{T}\gamma_\mu C\tau_{S} \lambda_{S^{\prime}} q)]. \end{aligned}\tag{A11} $

where the subscripts S and A are the symmetric and anti-symmetric indices, and C is a charge conjugation operator. In particular, we obtain
$ H:={\rm coeff}\; (\bar{q}{\rm i}\gamma_5 C\tau_{A} \lambda_{A^{\prime}}\bar{q}^{T})(q^{T}C i\gamma_5 C\tau_{A} \lambda_{A^{\prime}} q) = \frac{(N_c+1)g}{2N_c}. \tag{A12}$

For
$ N_c=3 $ , we obtain$ H=\dfrac{2}{3}g $ ; thus, the ratio$ H:G=\dfrac{(N_c)}{2(N_c-1)}=\dfrac{3}{4} $ .
Color-flavor dependence of the Nambu-Jona-Lasinio model and QCD phase diagram
- Received Date: 2022-01-26
- Available Online: 2022-08-15
Abstract: We study the dynamical chiral symmetry breaking/restoration for various numbers of light quarks flavors






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: