-
As a specific region of spacetime with strong gravitation, the black hole has always been a hot topic in astronomy and cosmology. For decades, many pioneering and important theoretical research and astronomical observations have been devoted to exploring the properties of black holes. Recently, the Laser Interferometer Gravitational Wave Observatory (LIGO) observed the gravitational wave from the merging of two black holes, which provides direct evidence of the existence of black holes [1–3]. In particular, the first ultra-high angular resolution image of a black hole in the center of galaxy M87* was captured by the Event Horizon Telescope Collaboration (EHT) [4–7]. The image shows a bright ring accompanied by a dark central area, where the bright ring is called the photon ring and the central dark area is the shadow of the black hole. This work not only shows the appearance of black holes visually, but also encourages the research of the black hole shadow.
The shadow is an important feature of a black hole, which could reveal the intrinsic structure of spacetime geometry around a black hole. In 1966, the theoretical analysis of the Schwarzschild black hole shadow formation was first proposed by Synge [8]. Soon after, the shadow of the Kerr black hole was discussed extensively in Refs. [9, 10], and the results showed that when the observer's position coincides with the equatorial plane, a D-shaped shadow will be obtained. Then, Luminet began to study the shadow of the Schwarzschild black hole surrounded by accretion disks, and the numerical simulation image of black hole was shown [11]. Indeed, the high-energy radiative materials around the black hole are the key factor to obtaining the shadow image [6, 12]. In Ref. [13], Cunha et al. found that the shadow of a black hole is affected by geometrically and optically thick accretion disks. By considering that the black hole is surrounded by an optically thin spherical accretion under different gravitational backgrounds, it can be seen that the position and radius of the photon sphere depend on the spacetime structure and are not affected by the behavior of the surrounding accretion [14–18]. In addition, Wald et al. investigated the shadow of a black hole that is surrounded by an optically thin disk accretion [18] and classified the ray trajectories near black holes into three types, namely direct emission, lensing rings, and photon rings. They found that the size and intensity of the bright ring are closely related to the location of the thin disk. In Ref. [19], Peng et al. discussed the shadow, photon rings, and lensing rings of the quantum-corrected Schwarzschild black hole to provide observational evidence for the quantum effect of general relativity. Taking into account this method, they also distinguish the observational feature of the asymmetric thin shell wormholes and black holes in Ref. [20]. Subsequently, the study of shadows and rings has been extended to rotating or non-rotating spacetime as well as other modified gravitational backgrounds [21–26].
As the basis of exploring a strong gravitational field, the shadow and observed appearance of the black hole have also been widely studied in general relativity [27–35] as well as in modified theory of gravity [36–43]. Extra dimensionality is an essential element of string theory [44–46]. It plays an important role in particle physics [45–50]. As a strong gravitational region, black holes have been used to probe potential effects of extra dimensions [51–55]. Recently, the observations of the black hole shadow provided a useful approach to study gravitational physics in high dimensions [56–58]. In the context of the Randall-Sundrum (RS) brane world, the existence of higher dimension spacetime will lead to the emergence of tidal charge [59–63]. In Ref. [64], Neves et al. used the shadow of the black hole to limit the tidal charge parameters in the Randall–Sundrum model and present an upper bound on the tidal charge. Furthermore, some interesting results of the black hole shadow in the Randall–Sundrum brane world can be found in Refs. [65, 66]. The black hole solution in Ref. [64] is similar to the Reissner–Nordström solution, and is just one solution of the gravitational field equation in the Randall–Sundrum model. A class of black hole solutions in a Randall–Sundrum brane have been investigated [67–69]. It is interesting to study the shadow of this black hole solution. The black hole solution proposed in Ref. [67] involves two intrinsic parameters, namely the tidal charge and the deformation parameter, C. The black hole solution [67] will return to a solution similar to that of the Reissner–Nordström solution. It is expected that changes in the structure or properties of the higher dimensions brane would lead to changes in the shadow and appearance of black holes in the observation of our four-dimensional-observable universe. In addition, the two parameters will affect the shadow radius and observation intensity of the black hole shadow [67]. The differences between the black hole shadow derived from the brane world and general relativity present direct evidence for searching for the signal of extra dimensions by future observations of EHT. In this study, for simplicity, we consider a black hole surrounded by an optically and geometrically thin spherical accretion where accretion radiation is the only background light source.
This paper is organized as follows. In Section II, the black hole solutions in the Randall–Sundrum scenario is introduced, and the equations of motion for photons are obtained. In Section III, we show the images of the black hole with spherically symmetric accretions. Finally, the discussions and conclusions are presented in Section IV.
-
The matter fields are confined to a four-dimensional hypersurface (the brane), which is a key feature of the brane-world model, while gravity propagates in a larger spacetime (the bulk). According to the method proposed by Shiromizu et al. [70], the effective four-dimensional gravitational field equation in a vacuum Randall-Sundrum brane is
$ R_{\mu \nu }-\frac{1}{2} R g_{\mu \nu }=-E_{\mu \nu }, $

(1) where R is the four-dimensional Ricci scalar. It is worth mentioning that the effective four-dimensional cosmological constant in the brane is null. Because
$ E_{\mu \nu } $ is the projection of the five-dimensional Weyl tensor on the brane, it is traceless in brane-world models. Then, we get$ R = 0. $

(2) In this work, we are interested in studying a black hole with spherically symmetric and static geometries. The bulk metric is of the form
$ {\rm d} s^2=-A(r) {\rm d} t^2 +B (r)^{-1}{\rm d} r^2 +r^2 {\rm d} \Omega^2, $

(3) where
${\rm d} \Omega^2={\rm d}\theta^2+\sin^2 \theta {\rm d}\phi^2$ is the line element on a unit sphere. Therefore, equation (2) can be written as a constraint between the functions$ A(r) $ and$ B(r) $ . It is given as$ 2(1-B)-r^2B\left[\frac{A^{\prime\prime}}{A}-\frac{\left(A'\right)^2}{2 A^2}+\frac{A'B'}{2 A B}+\frac{2}{r}\left(\frac{A'}{A}+\frac{B'}{B}\right)\right]=0, $

(4) where the primes denote the differentiation with respect to r. Based on the metric function given by equation (3), and the fact that equation (4) corresponds to the four dimensional Einstein equation with traceless energy momentum tensor, one solution of equation (4) is given as [59, 67]
$ A (r)= B(r) = A_0 (r),\quad A_0 (r)=1-\frac{2M}{r}+\frac{q}{r^2}. $

(5) Here, M is a constant and represents the mass of the black hole. It should be emphasized that despite the superficial similarity of the above solution, equation (5), with the Reissner-Nordström (
$ R-N $ ) metric, the charge parameter, q, results from the influence of the higher dimensional brane, which is called tidal charge. Specifically, the term q originates from the projection onto the brane of free gravitational field effects in the bulk, and these effects are transmitted via the bulk Weyl tensor. Moreover, in the vacuum brane, the tidal charge, q, is inherited from the nonlocal contributions of the bulk spacetime. In this solution, the tidal charge parameter, q, can assume both positive and negative values. Because there is no similar case of negative q in general relativity, it provides a true signature of the additional spatial dimensions [71–73]. In this system, the tidal charge parameter satisfies$ q<M^2. $

(6) Meanwhile, because equation (4) is linear for B, a linear combination of solutions with a fixed value of A is still a solution. In Refs. [67–69], the solution of equation (4) is given as
$ A (r)=A_0(r), $

(7) $ B(r)=A_0(r)+(C-1)B_{\rm lin}(r), $

(8) where C is constant and is called the deformation parameter of this solution. Here, the term
$B_{\rm lin}$ in equation (8) is of the form$ B_{\rm lin}(r)=\exp\left[-\int \frac{f (r)}{A_0 (r) h (r) } \, {\rm d}r\right], $

(9) where
$\begin{aligned}[b] f(r)=&A_0(r)A''_0(r) r - \frac{{A_0(r)}^2 r}{2 }+2 A_0(r)A'_0(r)+ 2\frac{{A_0(r)}^2 r}{r }, \end{aligned}$

(10) $ h(r)= \frac{A'_0(r) r}{2 }+2 A_0(r), $

(11) The value of the deformation parameter, C, has a certain influence on the geometric structure of spacetime. For the special case
$ C = 1 $ , it returns to the solution given by equation (5). For the case of$ C \geq 0 $ , it becomes a black hole spacetime with$ r_+=M+\sqrt{M^2-q} $ as the event horizon. Meanwhile, in the case of$ C<0 $ , the maximal extensions are wormhole solutions, which will not be considered in this paper.The trajectory of photons are described by the geodesic equations of a massless particle in spacetime, given by equation (3). Because the spacetime possesses spherical symmetry as given by equation (3), the trajectory of photons can be confined to the equatorial plane, i.e,
$ \theta=\dfrac{1}{2} \pi $ and$ \dot{\theta}=0 $ . In this context, the orbit of one particle in curved spacetime can be described by the Euler-Lagrange equation, that is$ \frac{{\rm d}}{{\rm d} \zeta }\left(\frac{\partial {\cal{L}}}{\partial \dot{x}^{\mu }}\right)=\frac{\partial {\cal{L}}}{\partial x^{\mu }}. $

(12) Here,
$ {\cal{L}} $ is the Lagrangian,$ \dot{x}^{\mu }=\dfrac{\partial x^{\mu}}{\partial \zeta} $ is the four-velocity of the photon, and ζ is the affine parameter. Hence, the Lagrangian,$ {\cal{L}} $ , for a particle is$ {\cal{L}} = \frac{1}{2} g_{\mu\nu} \dot{x}^{\mu } \dot{x}^{\nu }=\frac{1}{2} \left[-A(r) \dot{t}^2+\frac{\dot{r}^2}{B(r)}+r^2 \dot{\phi}^2\right]. $

(13) Because the metric coefficients of spacetime in equation (3) are independent of time, t, and azimuthal angle, ϕ, the two constants of motion, namely E and J, which are related to the energy and angular momentum, respectively, can be derived from the geodesic equations of spacetime given by equation (3). These constants are given as
$ E=A (r) \dot{t}, \quad J=r^2 \dot {\phi}. $

(14) Considering the null geodesic dynamics (
$ g_{\mu\nu} \dot{x}^{\mu } \dot{x}^{\nu }=0 $ ) in this spacetime, and replacing the affine parameter, ζ, with$ \zeta/|L| $ , we get$ \dot{t} = \frac{1}{b [A (r)]}, \quad \dot {\phi} = \pm\frac{1}{r^2},\quad \dot{r}^2=B(r)\left[\frac{1}{b^2 A(r)}-\frac{1}{r^2}\right]. $

(15) In order to show whether the direction of light is counterclockwise or clockwise, there is a ± sign before the azimuthal. Here, b is called the impact parameter, which is the ratio of angular momentum to energy, i.e.,
$ b\equiv J/E $ . There exists a critical curve, which is a circle having an apparent radius of$ b_c $ , and$ b_c $ is called the critical impact parameter. When traced backwards from the distant observer, the light ray from this critical curve will asymptotically approach a bound photon orbit, forming a closed surface, which is called photon sphere. The shadow of the black hole represents the dark interior of the critical curve, that is, the critical impact parameter,$ b_c $ , is the standard shadow radius of the black hole. In the photon sphere, the motions of the light rays follow the conditions$ \dot{r}^2=0 $ and$ \ddot{r}^2=0 $ , so that the radius of the photon sphere,$ r_{ph} $ , can be obtained by$ \left[\frac{A(r_{ph})}{r_{ph}^{2}}\right]'=0, $

(16) and the corresponding impact parameter,
$ b_c $ , is$ b_c=\frac{r_{ph}}{{A(r_{ph})}^{1/2}}. $

(17) In the equation, the prime represents the derivative with respect to
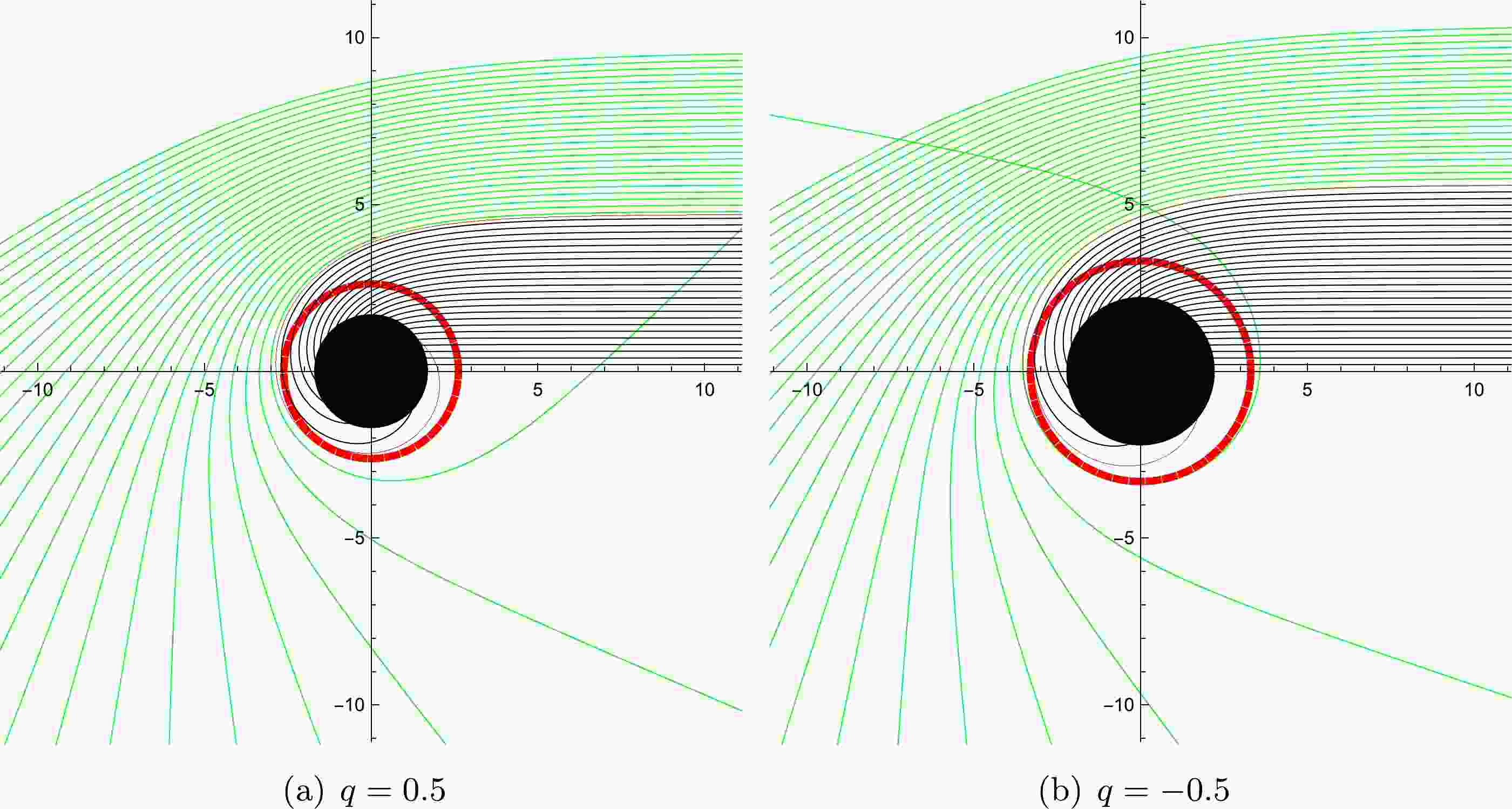
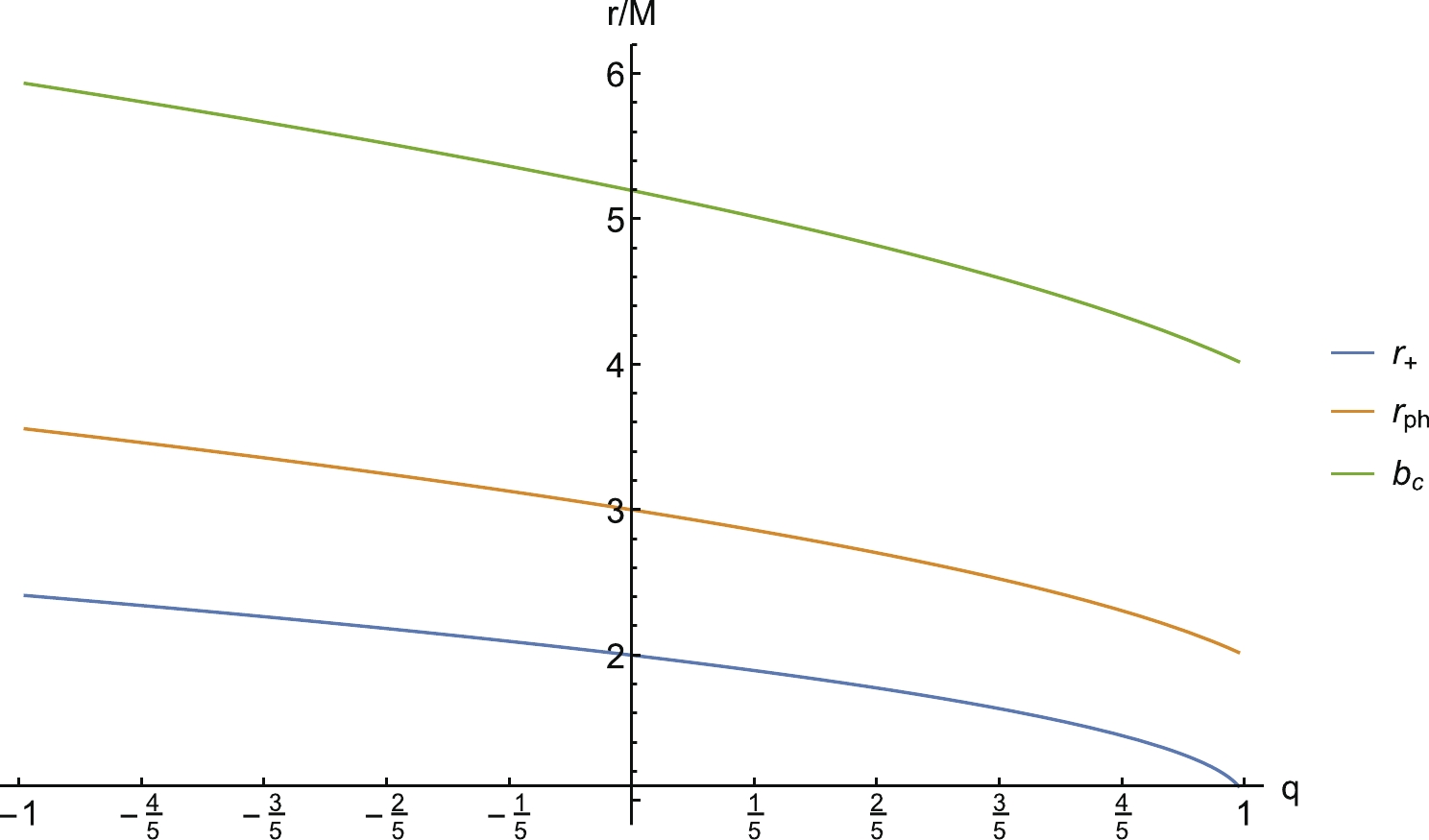
$ r_{ph} $ . From equation (17), the critical impact parameter,$ b_c $ , is a function of the radius of photon sphere,$ r_{ph} $ . When the value of tidal charge, q, increases, the value of the critical impact parameter,$ b_c $ , shows a decreasing trend, and the radius of photon sphere,$ r_{ph} $ , also decreases, which means that$ b_c $ and$ r_{ph} $ are positively correlated.In fact, the impact parameter, b, is defined as the perpendicular distance between the geodesic and a parallel line that passes through the origin, which means that the impact parameter can be regarded as the radial coordinate of the shadow image projected on the observer's screen. By employing the ray-tracing code, we can reveal the deflection of lights near the black hole, which is shown in Fig. 1. From Fig. 1, it can be seen that the path of light has a turning point that enables the photon to reach the observer at an infinite distance when
$ b > b_c $ ; this is indicated by the green lines. In contrast, when$ b < b_c $ , the photon will fall into the black hole and cannot reach an infinite distance, as indicated by the black lines. It should be noted that the critical impact parameter,$ b_c $ , depends completely on$ A (r) $ , not on$ B(r) $ [74]. In other words, the shape and size of the shadow depends only on the tidal charge, q, and the mass, M, of the black hole. The variation of relevant physical quantities with the change in tidal charge, q, is shown in Fig. 2. Fig. 2 shows that the presence of a negative tidal charge parameter enhances the size of the event horizon and photon sphere when compared to the one in the Schwarzschild black hole. The shadow size decreases with higher positive tidal charge.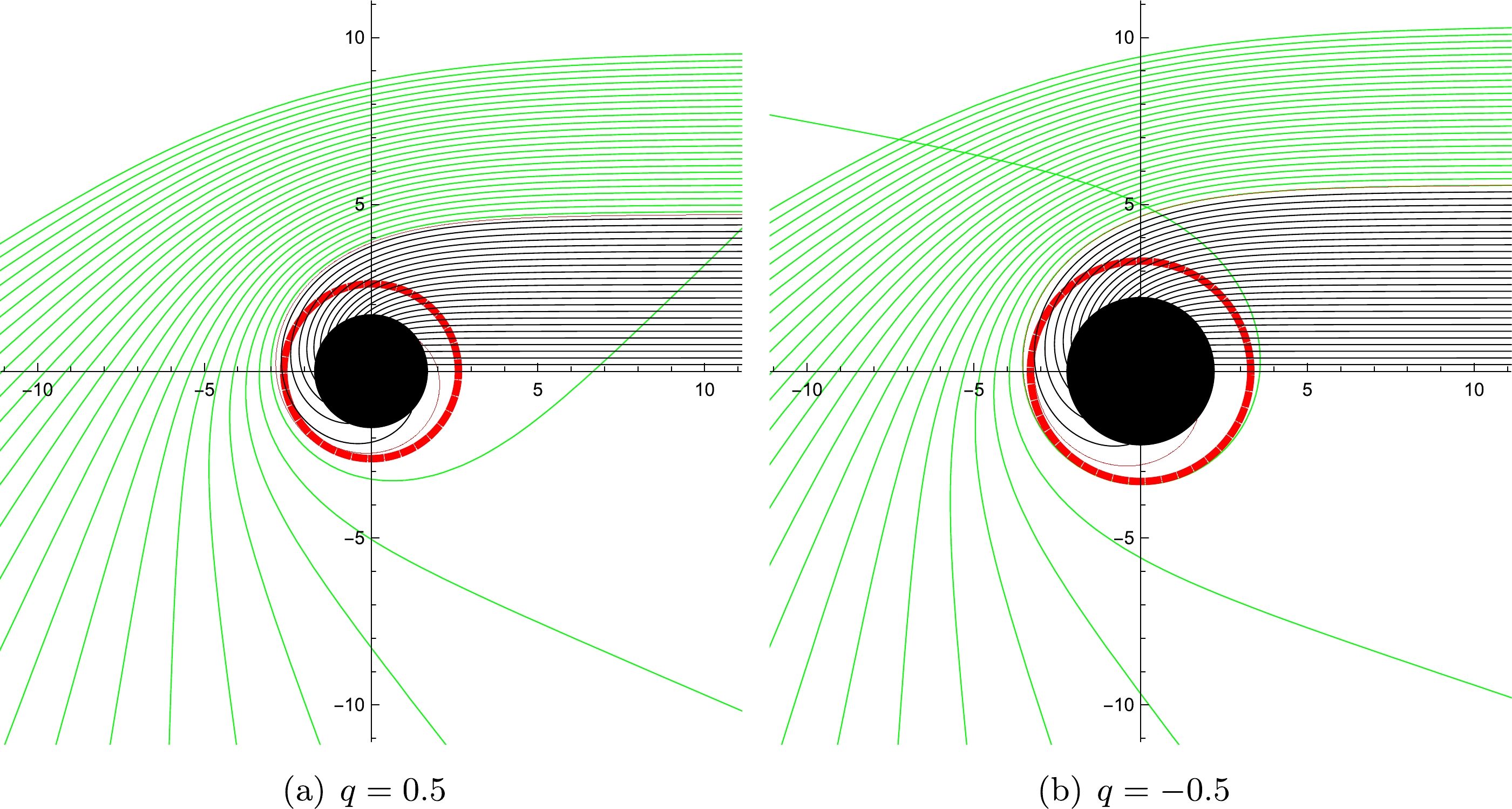
Figure 1. (color online) The trajectories of light rays for different values of q with
$ M=1 $ in the polar coordinates (r,ϕ), and the spacing of impact parameter, b, is 1/5. The dashed red line refers to the position of photon sphere, the red line refers to the critical curve, and the black solid disk represents the black hole. Panel (a) - the value of tidal charge parameter,$ q=0.5 $ . Panel (b)- the value of tidal charge parameter,$ q=-0.5 $ . -
The accretion material around the black hole plays an important role in determining the black hole image seen by distant observers. With the previous preparation, we can further study the shadow of a black hole surrounded by spherical accretion. In this study, we consider the brane-world black hole surrounded by spherical accretion, which is assumed to radiate isotropically in the rest frame of the matter. Meanwhile, the accretion free falls onto the black hole from infinity. This infalling model is thought to be more realistic than the static accretion model since most of the accretion matters are dynamic in the universe.
In the context of spacetime, as given by equation (3), we consider that the observed light intensity is mainly provided by the spherical accretion flow, which is optically and geometrically thin and evenly distributed outside the black hole. When our observer is at the North Pole, the simulation result of the black hole shadow is representative, and we can evolve light rays from the observer's position backwards in time. Following the definitions in Refs. [74, 75], by integrating the specific emissivity along the photon path, γ, we can obtain the observation specific intensity,
${I}_{{\rm obs}}$ (ergs−1cm−2str−1Hz−1) at the observed photon frequency,$\nu_{\rm obs}$ , which is$ {I}_{{\rm obs}}(\nu _{\rm obs})=\int _{\gamma}{g}^3 {j} (\nu _{em}) {\rm d} l_{{\rm prop}}, $

(18) and
$\begin{aligned}[b]g=\frac{k_{\rho}u^{\rho}_{\rm obs}}{k_{\sigma}u^{\sigma}_{em}},\;\;k^{\mu}\equiv \dot x_{\mu},\;\;u^{\mu}_{\rm obs}\equiv(1,0,0,0). \end{aligned} $

(19) Here, g is the redshift factor, and
$ k^{\mu } $ and$u_{\rm obs}^{\mu }$ represent the four-velocity of the photon and distant observer, respectively. In addition,$ \nu _{em} $ is the emitter photon frequency,$ {j} (\nu _{em}) $ is the emissivity per-unit volume at the emitter, and${\rm d} l_{{\rm prop}}$ is the infinitesimal proper length differential as measured in the frame comoving with the matter. The four-velocity of the infalling accretion is$ u_{em}^{\mu } $ $ u_{em}^t={A (r)}^{-1},\quad u_{em}^r=-\sqrt{\frac{1-A (r)}{A (r) B ( r)}}, \quad u_{em}^{\theta }=u_{em}^{\varphi }=0. $

(20) For the photons, we obtain
$ k_t $ as a constant of motion. From the null condition,$ k_{\mu }k^{\mu }=0 $ , we can obtain$ \frac{k_r}{k_t}=\pm \sqrt{B (r) \left(\frac{1}{A (r)}-\frac{b^2}{r^2}\right)}, $

(21) where the signs + and – correspond to the cases where the photon approaches and moves away from the black hole, respectively. According to the above equations, the redshift factor of the infalling accretion is
$ g=\left(u_{em}^t+\left(\frac{k_r }{k_{t}}\right)u_{em}^r \right) ^{-1}. $

(22) In general, we consider the emission of monochromatic light whose frequency is fixed to
$ \nu_f $ and the emission radial profile is$ 1/r^2 $ [74], namely$ {j} (\nu _{em})\propto\frac{\delta \left(\nu _{em}-\nu _f\right)}{r^2}, $

(23) where δ denotes the delta function. From equation (3), the expression of the corresponding proper distance is
$ {\rm d} l_{\rm prop}=k_\sigma u_{em} ^\sigma {\rm d}\lambda=\frac{k_t}{g |k_r|} {\rm d} r, $

(24) where λ is the affine parameter along the photon path, γ, in the case of the free-fall model. Hence, the intensity observed flux with infalling spherical accretion,
${I}_i (\nu_{\rm obs})$ , can be expressed as$ {I}_i (\nu_{\rm obs})\propto \int _{\gamma}\frac{g^3 k_t {\rm d} r}{r^2 |k_r|}. $

(25) It can be seen that the total observed flux obtained by the observer is determined by both
$ A (r) $ and$ B(r) $ , and${I}_i (\nu_{\rm obs})$ is still a function of the impact parameter, b. Therefore, the change in related state parameters has a more direct influence on the black hole shadow image. To intuitively show the kind of influence, we plot the variation of the specific intensity,${I}_i (\nu_{\rm obs})$ , with the impact parameter, b, under different state parameter values in Fig. 3. It should be noted that we still assume that the observer is located in the North Pole, i.e., this is viewed in a face-on orientation from the equatorial plane of the black hole.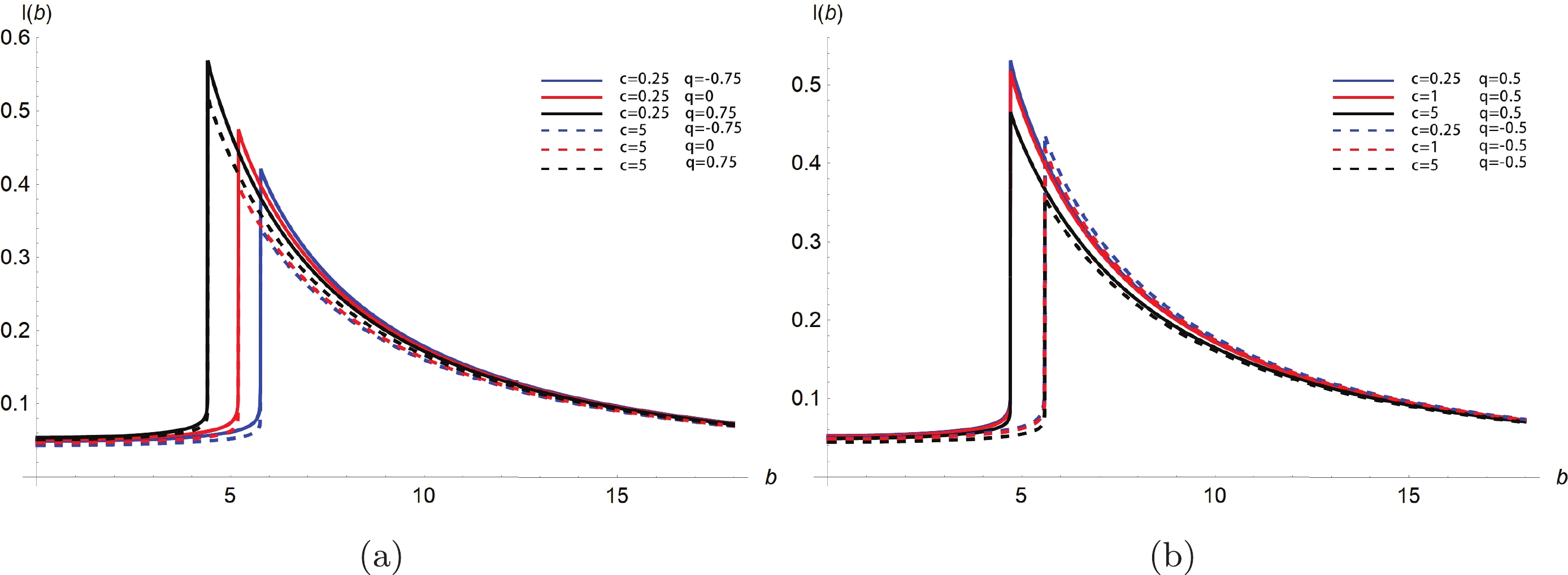
Figure 3. (color online) Profiles of the specific intensity seen by a distant observer under the different relevant state parameters in which
$ M=1 $ . Panel$ (a) $ - Various tidal charges$ q= -0.75, 0, 0.75 $ with$ C=0.25 $ (the solid line) and$ C=5 $ (the dotted line). Panel$ (b) $ - Various parameters$ C=0.25, 1, 5 $ with the positive tidal charge$ q=0.5 $ (the solid line) and the negative tidal charge$ q=-0.5 $ (the dotted line).Owing to the numerical limitations and the logarithmic form of intensity, the actual computed intensity never goes to infinity; this has also been well addressed in Refs. [74, 75]. As illustrated in Fig. 3, when the impact parameter, b, increases, the observed strength,
${I}_i (\nu_{\rm obs})$ , begins to increase slowly; however, it increases sharply near the critical impact parameter,$ b_c $ , until it reaches its peak at the position$ b=b_c $ and then shows an attenuation trend. The light ray will rotate around the black hole many times at the position$ b = b_c $ and collect an arbitrarily large intensity so that the observed intensity at the position,$ b_c $ , is the largest. When$ b < b_c $ , the strong gravity of the black hole causes the light intensity produced by the accretion material to be swallowed by the black hole, which leads to the observed intensity to be extremely small. Meanwhile for$ b > b_c $ , although the refracted light can reach the distant observer, the increase in b causes the refracted light to becomes less, which makes the observed intensity become weaker. With a fixed value of parameter C, the results show that the observation intensity under positive tidal charge is greater than that when the tidal charge parameter is negative. That is, the increase in tidal charge, q, will increase the peak value of observation intensity, although the radius of the black hole shadow will become smaller. In addition, the peak value of observation intensity decreases with the increase in parameter C when the value of tidal charge, q, is fixed.Furthermore, the images of the optically thin emission region around the black hole are also shown in Fig. 4 and Fig. 5. When the value of tidal charge, q, is fixed (
$ q=-0.5 $ or$ q=0.5 $ ), the black hole shadow image darkens with the increase in parameter C; however, the shadow radius and the photon ring size do not change. That is, the change in parameter C will only change the observation intensity; it will not affect the radius of the black hole shadow or the position of the photon sphere. For a fixed value of parameter C ($ C=0.25 $ or$ C=5 $ ), the luminosity increases with an increase in the tidal charge, q, and the bright area outside the black hole shadow also expands. As a result, the change in tidal charge, q, affects the radius of the shadow, the position of the photon sphere, and the intensity of the observation.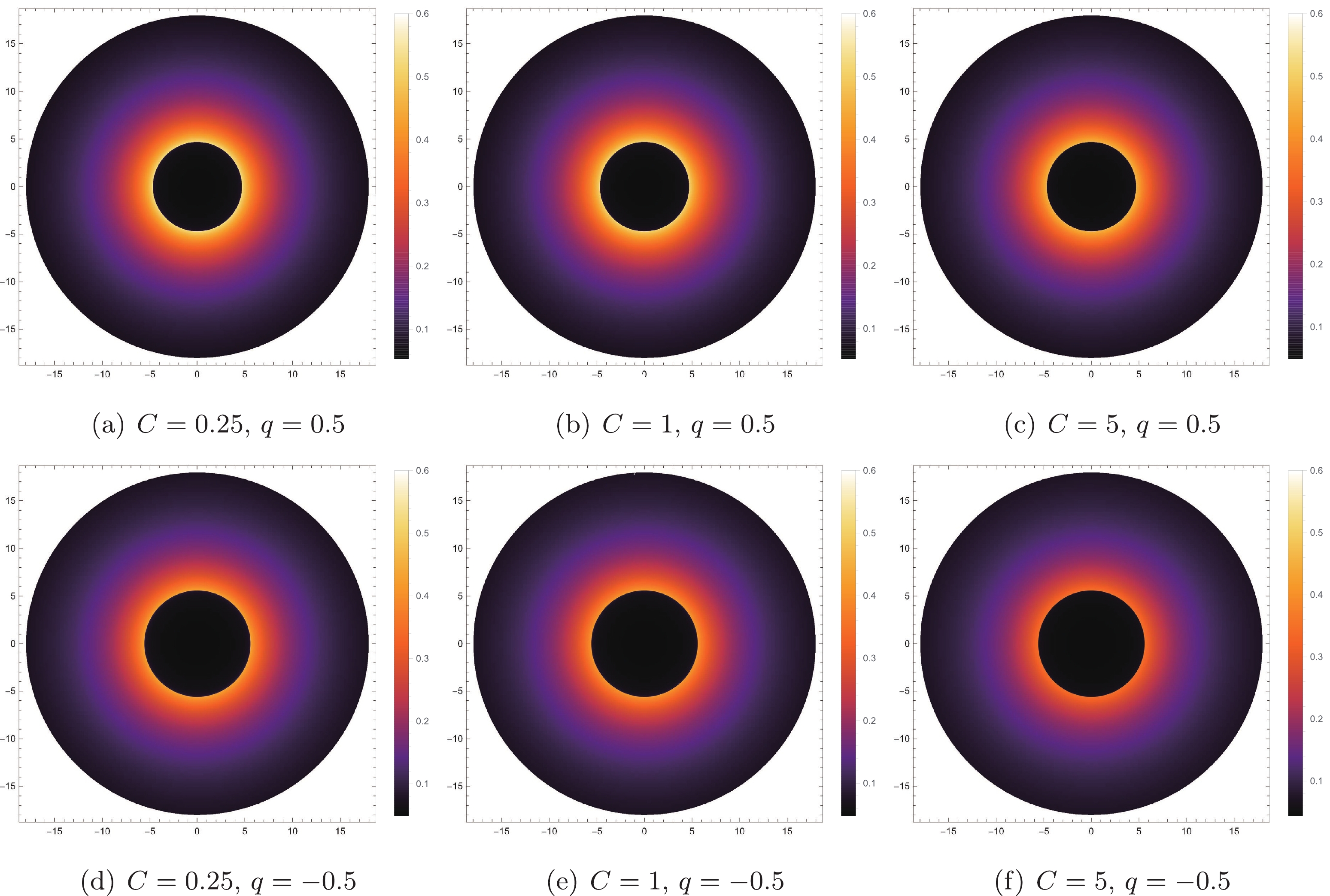
Figure 4. (color online) Image of the black hole shadow with the infalling spherical accretion flow for the different values of C, in which
$ M=1 $ . In the first row, we take$ q = 0.5 $ , and in the second row, we take$ q=-0.5 $ .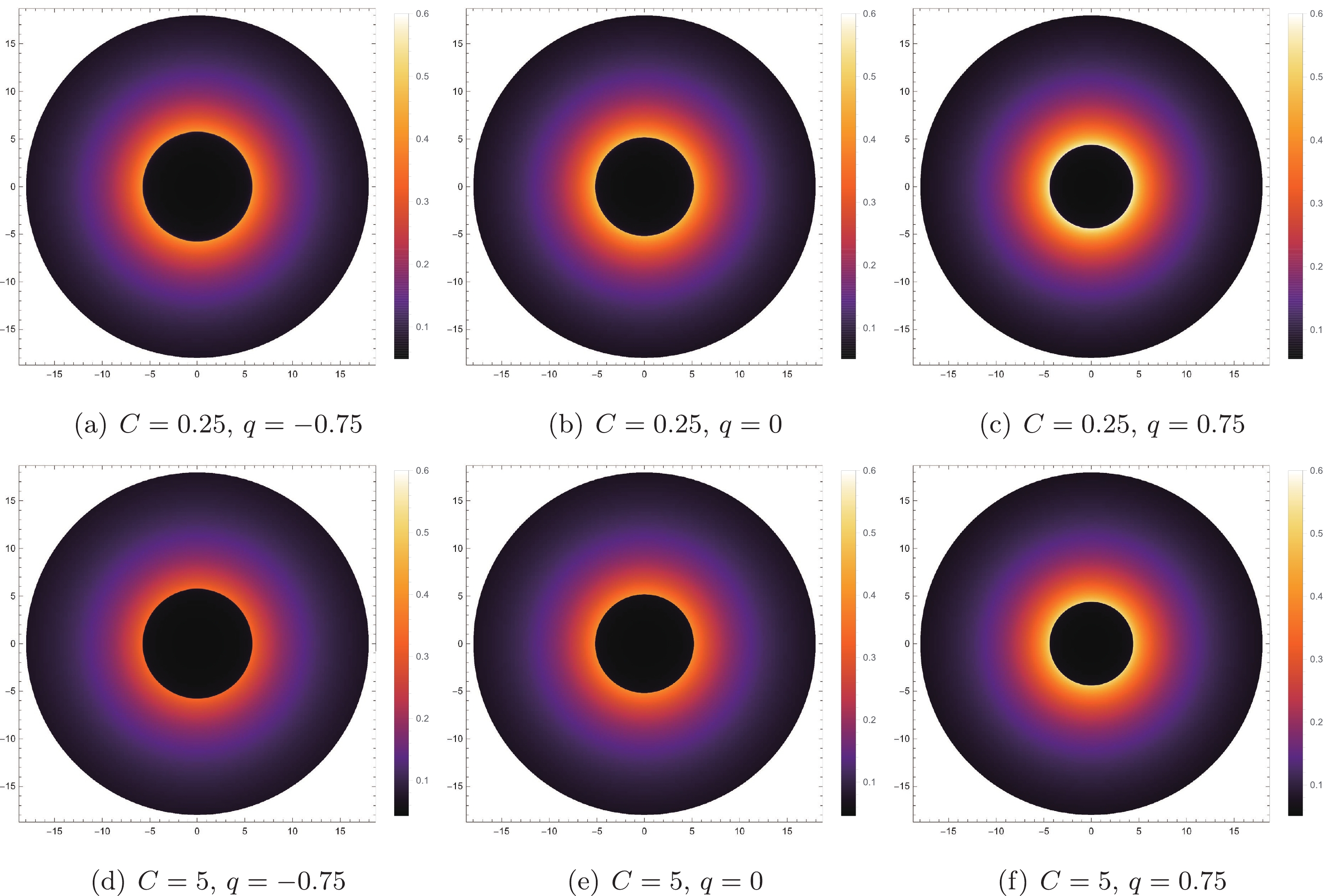
Figure 5. (color online) Image of the black hole shadow with the infalling spherical accretion flow for the different values of q, in which
$ M=1 $ . In the first row, we take$ C = 0.25 $ , and in the second row, we take$ C = 5 $ .On comparing the results in Figs. 4, and 5, we can see that the degree of influence of these two parameters (q and C) on the observation intensity is different. As shown by the blue solid line (
$ C=0.25 $ ,$ q=-0.75 $ ) and blue dotted line ($ C=5 $ ,$ q=-0.75 $ ) in the left panel of Fig. 3, the increase in the value of parameter C reduces the peak value of observation intensity. However, with the increase in tidal charge, q, the peak value of the black dotted line ($ C=5 $ ,$ q=0.75 $ ) becomes higher than that of the blue solid line. That is, the influence of parameter C on the observation intensity is not only loosening, but also enhancing the final observation intensity. In short, the observation intensity is mainly influenced by the tidal charge parameter, q, and parameter C is of secondary importance. -
In this study, we investigated the behavior of the photon sphere and shadow of a black hole surrounded by optically thin accretion embedded in the Randall–Sundrum brane model and explored the optical appearance characteristics of the black hole shadow. In the context of the Randall–Sundrum brane world scenario, the non-trivial effects are inherited from the bulk, the effective gravitational field equations on the brane are modified, and these modifications are manifested in the brane localized black hole solution as the tidal charge. Because the four-dimensional killing horizon (event horizon) geometry structure of the brane-world black hole is affected by changes in the tidal charge parameter, q, the critical impact parameter,
$ b_c $ (the shadow radius of the black hole) is closely related only to the metric coefficient,$ A (r) $ , of a four-dimensional hypersurface as in equation (3). In the case of$ q<0 $ , the critical impact parameter,$ b_c $ , has a greater value than its Schwarzschild counterpart, i.e., the emergence of negative tidal charge makes the black hole cast a larger shadow area. For the case of$ q>0 $ , the radius of the black hole shadow is always smaller than that of the Schwarzschild spacetime ($ q=0 $ ,$ C=1 $ ). Hence, the increase in q reduces the radius of black hole shadow.In the system we investigated, both tidal charge, q, and deformation parameter, C, can affect the geometry structure of spacetime, which means that the observation light intensity obtained by the observer highly depends on these two parameters. Therefore, we numerically calculated the variation of observation intensity under different parameter values and provided the profile image of black hole shadow. Specifically, the peak value of observation intensity increases with the increase intidal charge, q, i.e., the optical observation appearance of black holes is brighter when the tidal charge parameter takes a larger value. Although the range of the shadow decreases, the range of the bright area outside the shadow increases with the increase in tidal charge, q. In addition, it is also found that the peak value of observation intensity shows a downward trend with the increase in parameter C when the tidal charge, q, takes a quantitative value, and the range of bright areas outside the shadow also decreases. In conclusion, the shadow of the black hole embedded in the Randall–Sundrum brane model is very different from the one in the Schwarzschild black hole. These differences can be used to search for signs of extra dimensions in future observations of a black hole shadow.
Shadows and observation intensity of black holes in the Randall–Sundrum brane world model
- Received Date: 2022-01-18
- Available Online: 2022-07-15
Abstract: The shadow and observation intensity of a black hole surrounded by a thin spherical accretion in the Randall–Sundrum brane world model are investigated. The bulk metric depends on the tidal charge parameter, q, and deformation parameter, C. It reduces to the metric that possesses similar form with the Reissner–Nordström metric if





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: