-
Chirality is a subject of general interest in physics, chemistry, and biology. Chirality in atomic nuclei was predicted in 1997 [1], which has been a prominent topic for the past two decades. In the rotating triaxial nucleus with the unpaired particle(s) and hole(s) in the high-j orbital, the particle(s) and hole(s) align their angular momentum vectors along the short and long axes, respectively, while the collective rotation vector of the core aligns along the intermediate axis, which can form a chiral system. Due to quantum tunneling, a pair of nearly degenerate
$ \Delta I=1 $ bands with the same parity, i.e., chiral doublet bands, can be observed experimentally [1]. Since the chiral doublet bands were first observed experimentally [2], more than 50 candidates have been reported in the$ A\sim $ 80,100,130, and 190 [3–11] mass regions. In 2006, Meng et al. [12] suggested that more than one pair of chiral doublet bands can exist in one single nucleus, which are called multiple chiral doublet (MχD) bands. To date, experimental evidence for the MχD bands has been observed in 78Br [13], 81Kr [9], 103Rh [14], 105Rh [15, 16], 107Ag [17–19], 133Ce [20], 135Nd [21, 22], 136Nd [23], and 195Tl [24]. Theoretically, since the chiral symmetry breaking was first predicted using the tilted axis cranking (TAC) approach and particle-rotor model (PRM) [1], numerous efforts have been devoted toward the development of the TAC [25–29] and PRM methods [25, 26, 30–50] to describe chiral rotation in atomic nuclei. Meanwhile, the interacting boson-fermion model approach [51, 52], collective Hamiltonian method [53, 54], angular momentum projection method [55, 56], random phase approximation [57], and critical point symmetries method [58] have also been developed to study chiral doublet bands and have yielded considerable success. An overview of these studies and open problems for understanding the nuclear chirality are introduced in Refs. [3–5, 7].So far, many candidate chiral nuclei have been reported in the 80,100, and 130 mass regions [6, 7], forming three "islands of chiral nuclei". In comparison, only five candidate chiral nuclei have been reported in the 190 mass region, namely,
$ ^{193,194,195,198} $ Tl [24, 59–65] and 188Ir [66]. In 2008, candidate chiral doublet bands with the$\pi h_{9/2}^1\otimes \nu i_{13/2}^{-1}$ configuration were observed in 198Tl [64]. The two-quasiparticle-plus-triaxial-rotor model calculations suggested an aplanar orientation of the total angular momenta for these bands, thus supporting possible chirality [64, 65]. From 2011 to 2014, a pair of rotational bands associated with the$ \pi h_{9/2}^1\otimes \nu i_{13/2}^{-1} $ configuration at lower spins and the$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-3} $ configuration at higher spins were reported in 194Tl [61–63]. These bands were suggested as chiral geometry in the angular momentum space owing to their near-degeneracy in the excitation energies and similar alignments and$ B(M1)/B(E2) $ reduced transition probability ratios [61–63]. The chirality in 194Tl was also supported by the two-quasiparticle-plus-triaxial-rotor model and Cranked Nilsson Strutinsky model [61–63].In 2017, three negative-parity bands based on the
$ \pi h_{9/2}^1\otimes \nu i_{13/2}^{-2} $ configurations with close excitation energies and almost equal$ B(M1)/B(E2) $ values were identified in 193Tl, which suggested that one or two chiral systems were formed [59]. Theoretical calculations with the Cranked Nilsson Strutinsky model suggested the triaxial shape of 193Tl and thus supported the presence of chirality [59, 60]. In 2018, two pairs of nearly degenerate bands based on the$ \pi h_{9/2}^1\otimes \nu i_{13/2}^{-2} $ and$ \pi i_{13/2}^1\otimes \nu (fp)^{1} i_{13/2}^{-3} $ configurations were identified in 195Tl [24], which signified the first evidence of MχD in the 190 mass region. The Total Routhian surface (TRS) and relativistic mean field (RMF) calculations predicted triaxial shapes for both configurations [24, 50].It is naturally interesting to search for and predict the chirality or MχD phenomenon of thallium isotopes in the A
$ \sim $ 190 mass region. The triaxial deformation and suitable unpaired high-j particles-holes configurations are necessary for the prediction of the candidate chiral nuclei, which can be obtained from the fully microscopic self-consistent RMF theory [67]. The RMF has obtained great success in predicting and describing interesting physics [68–79]. Thus, we adopt the constrained triaxial RMF theory to search for the candidate nuclei of chirality and MχD in thallium isotopes. -
The starting point of the RMF theory is the standard effective Lagrangian density constructed with the degrees of freedom associated with a nucleon field (ψ), two isoscalar meson fields (σ and
$ \omega_\mu $ ), the isovector meson field ($ \vec{\rho}_\mu $ ), and the photon field ($ A_\mu $ ). This theory has been successfully applied to study triaxial shape coexistence and possible MχD in many nuclei, e.g., Co isotopes [80], As isotopes [81], Br isotopes [82], Rb isotopes [83],$ ^{104,106,108,110} $ Rh [84, 85],$ ^{103,105} $ Rh [86, 14], 107Ag [87],$ ^{125,129,131} $ Cs [88], 133Ce [20], and 195Tl [50]. Here, only a brief introduction to the triaxial RMF is provided; a detailed formalism can be found in Ref. [12]. Under the “mean-field” and “no-sea” approximations, one can derive the corresponding energy-density functional, from which one can obtain the equation of motion for a single-nucleon orbit$ \psi_i (\boldsymbol{r}) $ with the help of the variational principle$ \{\alpha\cdot [ \boldsymbol{p}-\boldsymbol{V}(\boldsymbol{r})]+\beta m^{*}(\boldsymbol{r})+V_{0}(\boldsymbol{r})\}\psi_{i}(\boldsymbol{r})=\epsilon_{i}\psi_{i}(\boldsymbol{r}). $

(1) Here,
$ m^{*}(\boldsymbol{r}) $ is defined as$ m^{*}(\boldsymbol{r})\equiv m+g_{\sigma}\sigma(\boldsymbol{r}) $ , with m referring to the mass of the bare nucleon. The repulsive-vector potential$ V_{0}(\boldsymbol{r}) $ , i.e., the time-like component of the vector potential is given by$ V_{0}(\boldsymbol{r})=g_{\omega}\omega_{0}(\boldsymbol{r})+g_{\rho}\tau_{3}\rho_{0}(\boldsymbol{r})+e\frac{1-\tau_{3}}{2}A_{0}(\boldsymbol{r}), $

(2) where
$ g_\sigma, g_\omega, g_\rho $ are the coupling strengths between the nucleons and mesons, and$ \tau_3=1 $ ($ -1 $ ) for neutrons (protons). The time-odd fields$ \boldsymbol{V}(\boldsymbol{r}) $ are given by the space-like components of the vector fields$ \boldsymbol{V}(\boldsymbol{r})=g_{\omega}\boldsymbol{\omega}(\boldsymbol{r})+g_{\rho}\tau_{3}\boldsymbol{\rho}(\boldsymbol{r})+e\frac{1-\tau_{3}}{2}\boldsymbol{A}(\boldsymbol{r}). $

(3) Each Dirac spinor
$ \psi_{i}(\boldsymbol{r}) $ is expanded in terms of a set of three-dimensional harmonic-oscillator (HO) bases in Cartesian coordinates with 12 major shells. The meson fields that provide the nuclear mean-field potentials are expanded in terms of the same HO basis as these Dirac spinors but with 20 major shells. Due to the Pauli block effect, pairing correlations are neglected.The calculated results with the parameter set PK1 [89] are shown in this paper, and it has been verified that a very similar conclusion can be obtained adopting the NL3 [90], PC-PK1 [78] parameter sets. We use constrained calculation with
$ \langle\hat{Q}_{20}^{2}+2\hat{Q}_{22}^{2}\rangle $ , i.e.,$ \beta_2^2 $ , to find the ground state of triaxial deformed nuclei. In the process of the β-constrained calculation, triaxial deformation is automatically obtained by minimizing the energy. During the calculation, different configurations can be obtained by adiabatic constrained calculation, and then, the configuration-fixed constrained calculation is performed. Here, the adiabatic constrained calculation indicates that the nucleon always occupies the lowest single-particle levels, while the configuration-fixed constrained calculation suggests that the nucleon must occupy the same combination of the single-particle levels during the constraint process [12, 84]. -
The calculated potential-energy curves for the odd-odd nuclei
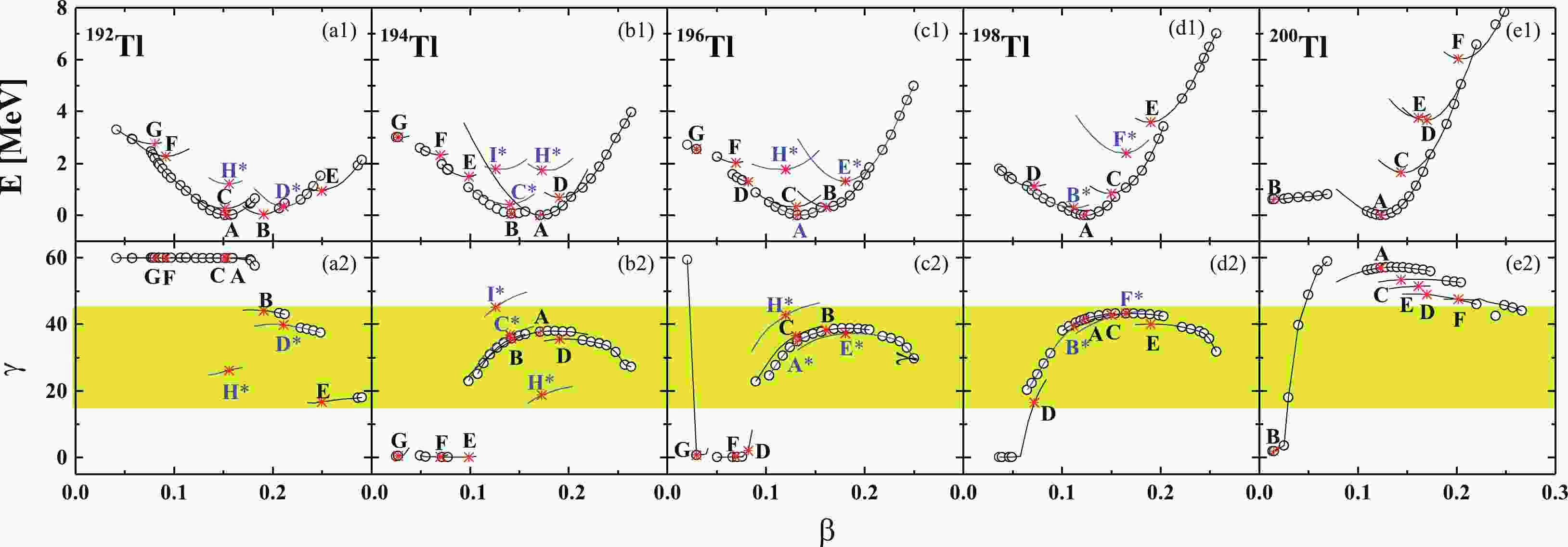
$ ^{192,194,196,198,200} $ Tl, based on the adiabatic and configuration-fixed constrained triaxial RMF theory, are presented in the upper panel of Fig. 1, while the results for the odd-mass nuclei$ ^{193,195,197,199} $ Tl are presented in the upper panel of Fig. 2. The minima in the potential-energy curves for the fixed configurations are represented by stars and labeled as A to J. The triaxiality parameter γ obtained by minimizing the energy is given as a function of β in the lower panel of Fig. 1 and Fig. 2. The shaded areas in the figures represent the triaxiality parameter γ favorable for nuclear chirality. In our calculations, the quadrupole deformation parameter β is constrained from 0 to 0.5. As there are no suitable chiral configurations for$ \beta> 0.3 $ , only the results of$ \beta < 0.3 $ are exhibited here.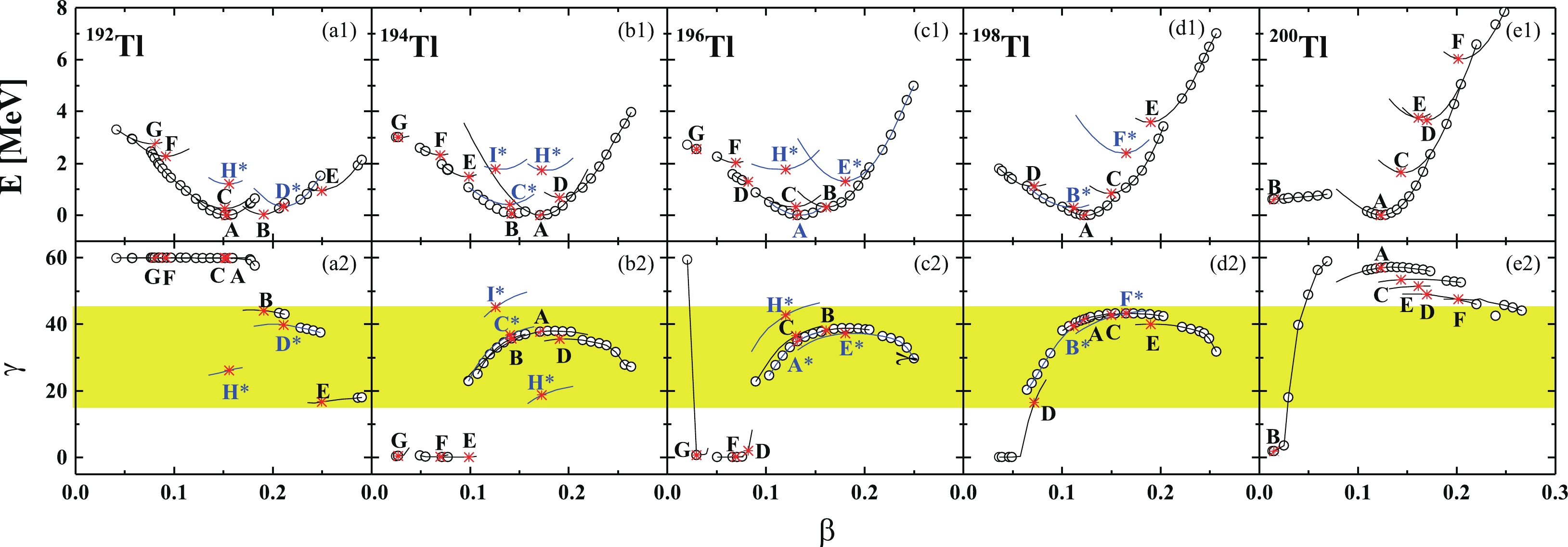
Figure 1. (color online) The calculated potential-energy curves E (in MeV) and triaxiality parameter γ (in degrees) as functions of the deformation parameter β for the odd-odd nuclei
$ ^{192,194,196,198,200} $ Tl. The open circles and solid lines represent the results for the adiabatic and configuration-fixed constrained triaxial RMF calculations with the PK1 parameter set. The minima in the energy curves for the fixed configuration are represented by stars and labeled as A, B, C, D, E, F, G, and H, respectively. The suitable states for the appearance of chirality are marked in blue with asterisks. The shaded area represents the triaxiality parameter γ, favorable for nuclear chirality.
Figure 2. (color online) Same as Fig. 1, but for the odd-mass nuclei
$ ^{193,195,197,199} $ Tl.As triaxial deformation is the necessary condition for nuclear chirality, we first search for the minima with prominent triaxial deformation. As shown in Fig. 1 and Fig. 2, more than one triaxial local minimum is found in
$ ^{192,193,194,195,196,197,198} $ Tl, which provide good examples of triaxial shape coexistence. As the neutron number increases, the quadrupole deformation parameter of the ground states in the Tl isotopes decreases, and the energy of the excited states increases. For 199Tl, the calculations show that there is no suitable triaxial minimum, although the 3-quasiparticle band based on the$\pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-2}$ configuration has been observed experimentally [91]. For 200Tl, the oblate band based on the high-j particle hole configuration$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1} $ has been extended beyond the particle alignment frequencies [92], and our results also show that there is no suitable triaxial deformation in these nuclei. Therefore,$ ^{199,200} $ Tl can be ruled out from the suggested candidate chiral nuclei.Apart from triaxial deformation, the proper particles-holes configuration is also necessary for the appearance of the chiral doublet bands. By performing the configuration-fixed constrained calculations, the single-particle levels for a certain configuration can be obtained as functions of the deformation β [12]. Considering the ground state and excited states with particle-hole configurations of 194Tl and 199Tl as examples, the proton and neutron single-particle levels obtained are presented in Fig. 3. The positive (negative) parity states are marked by solid (dashed) lines and the occupations of the ground states are represented by filled circles (two particles) and stars (one particle). The corresponding quantum numbers for the spherical case are labeled on the left side of the levels.
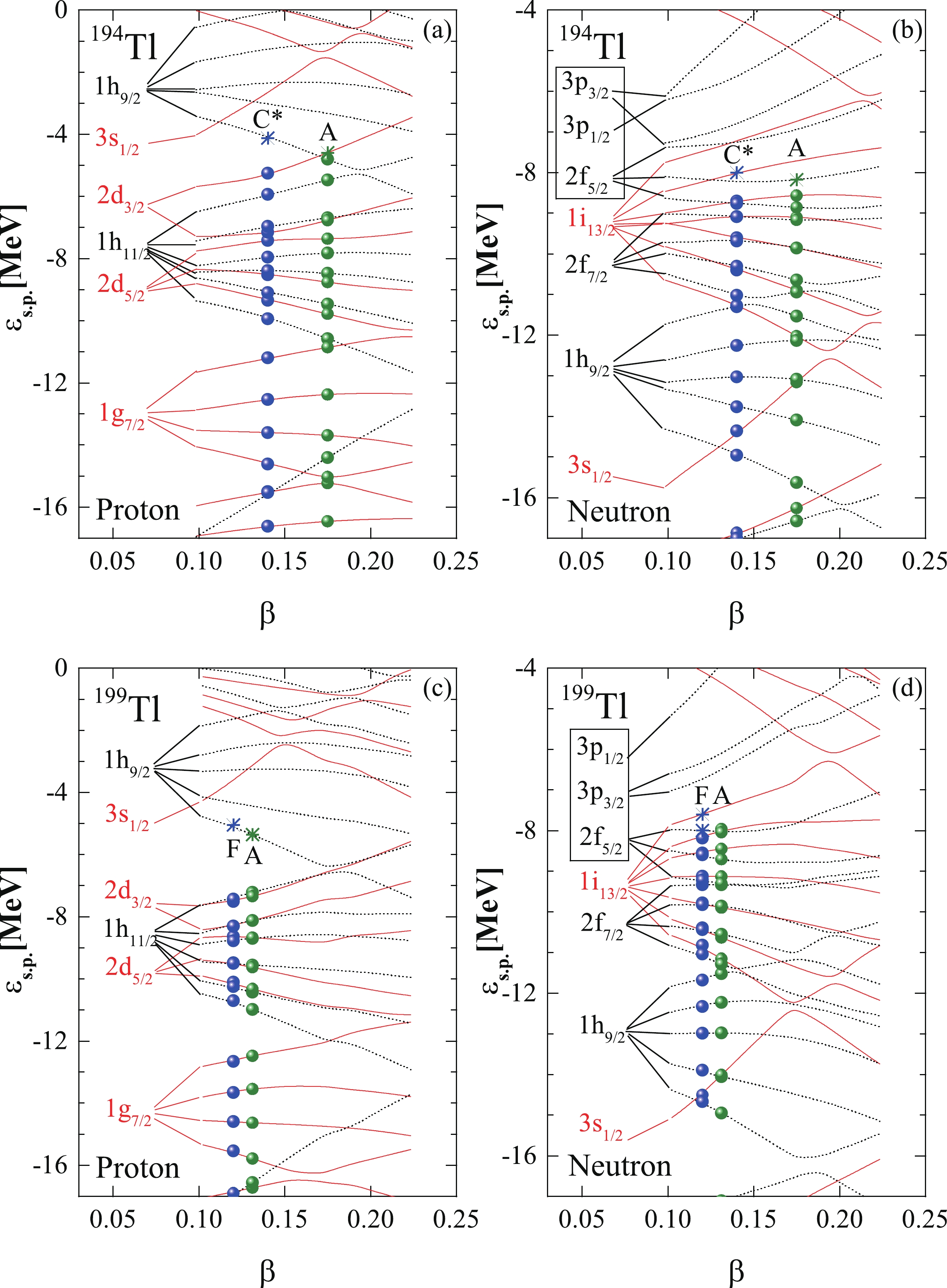
Figure 3. (color online) Proton and neutron single-particle levels obtained for constrained triaxial RMF calculations as functions of the deformation β for the ground state and excited states with particle-hole configurations of 194Tl (upper panel) and 199Tl (lower panel). The positive (negative) parity states are marked by solid (dot) lines and the occupations of the ground states (olive) and excited states (blue) are represented by filled circles (two particles) and stars (one particle).
The calculated total energies
$E_{\rm tot}$ , excited energies relative to the ground state$E_x({\rm cal.})$ , triaxial deformation parameters β and γ, corresponding valence nucleon, and unpaired nucleon configurations of the minima are given in Tables 1 and 2. The valence proton configurations take reference of 82 nucleons, which occupy the states below the 82 major-shell. The valence neutron configurations take reference of 114 nucleons, which occupy the states below the 126 major-shell except for the$ 3p_{3/2} $ ,$ 3p_{1/2} $ , and$ 2f_{5/2} $ subshells. As it is difficult to distinguish the occupation in the low-j orbits$ 3p_{3/2} $ ,$ 3p_{1/2} $ , and$ 2f_{5/2} $ , we denote the nucleons in the three subshells as$ (fp)^{n} $ in the tables. As the nuclear chirality of thallium isotopes is essentially determined by the high-$j $ $ 1i_{13/2} $ and$ 1h_{9/2} $ , such illegibility does not influence the conclusions drawn here. Combining the calculated deformations and configurations, we find the suitable states for the appearance of chirality, which are marked in blue with asterisks in the Figures and Tables. In what follows, the possible candidate states of chirality and MχD in thallium isotopes are discussed for odd-odd and odd-mass nuclei, respectively.Nuclei States Configuration $E_{\rm tot}$ 

/MeV( $ \beta, \gamma $ )

$ E_{x}(\rm cal.) $ 

/MeVValence nucleons Unpaired nucleons 192Tl A $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{3} i_{13/2}^{-6}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (fp)^1 $ 

−1506.26 (0.15,59.82 $ ^\circ $ )

0 B $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{2}i_{13/2}^{-5}] $ 

$ \pi d_{3/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1506.23 (0.19,44.15 $ ^\circ $ )

0.03 C $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}i_{13/2}^{-5}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1506.00 (0.15,59.94 $ ^\circ $ )

0.26 D* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{2}i_{13/2}^{-5}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1505.92 (0.21,39.84 $ ^\circ $ )

0.34 E $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{11/2}^{-2}h_{9/2}^{5})\otimes\nu[f_{7/2}^{-2}(fp)^{3}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes \nu (fp)^1 $ 

−1505.32 (0.25,16.72 $ ^\circ $ )

0.94 F $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{2}i_{13/2}^{-5}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1503.99 (0.09,59.93 $ ^\circ $ )

2.27 G $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{1}i_{13/2}^{-4}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu (fp)^1 $ 

−1503.50 (0.08,59.94 $ ^\circ $ )

2.76 H* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [f_{7/2}^{-2}(fp)^2i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1505.06 (0.16,26.17 $ ^\circ $ )

1.20 194Tl A $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{3}i_{13/2}^{-4}] $ 

$ \pi d_{3/2}^{-1}\otimes\nu (fp)^{1} $ 

−1523.19 (0.17,37.74 $ ^\circ $ )

0 B $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{3}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (fp)^{1} $ 

−1523.12 (0.14,35.68 $ ^\circ $ )

0.07 C* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1522.77 (0.14,36.81 $ ^\circ $ )

0.42 D $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{3}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (fp)^1 $ 

−1522.51 (0.19,35.61 $ ^\circ $ )

0.68 E $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{2}i_{13/2}^{-3}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1521.79 (0.10,0.19 $ ^\circ $ )

1.49 F $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{1}i_{13/2}^{-2}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu (fp)^{1} $ 

−1520.86 (0.07,0.27 $ ^\circ $ )

2.33 G $ \pi(s_{1/2}^{-1})\otimes\nu [i_{13/2}^{-1}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1520.19 (0.03,0.47 $ ^\circ $ )

3.00 H* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{2}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1521.46 (0.17,18.80 $ ^\circ $ )

1.73 I* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1}i_{13/2}^{-1}i_{13/2}^{-1} $ 

−1521.42 (0.13,45.19 $ ^\circ $ )

1.78 196Tl A* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1539.43 (0.13,34.88 $ ^\circ $ )

0 B $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{4}i_{13/2}^{-3}] $ 

$ \pi d_{3/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1539.12 (0.16,38.25 $ ^\circ $ )

0.31 C $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{3}i_{13/2}^{-2}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (fp)^{1} $ 

−1539.11 (0.13,36.56 $ ^\circ $ )

0.32 D $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{3}i_{13/2}^{-2}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu (fp)^{1} $ 

−1538.15 (0.08,2.10 $ ^\circ $ )

1.28 E* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1538.12 (0.18,37.26 $ ^\circ $ )

1.31 F $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{2}i_{13/2}^{-1}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1537.40 (0.07,0.21 $ ^\circ $ )

2.03 G $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{1}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu (fp)^{1} $ 

−1536.88 (0.03,0.77 $ ^\circ $ )

2.55 H* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1,537.67 (0.12,42.75 $ ^\circ $ )

1.77 198Tl A $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{5}i_{13/2}^{-2}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (fp)^{1} $ 

−1555.14 (0.12,41.49 $ ^\circ $ )

0 B* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1554.86 (0.11,39.43 $ ^\circ $ )

0.28 C $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{5}i_{13/2}^{-2}] $ 

$ \pi d_{3/2}^{-1}\otimes\nu (fp)^{1} $ 

−1554.30 (0.15,42.84 $ ^\circ $ )

0.84 D $ \pi(s_{1/2}^{-1})\otimes\nu[(fp)^{4}i_{13/2}^{-1}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1554.02 (0.07,16.54 $ ^\circ $ )

1.12 E $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-2}i_{11/2}^{1}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{11/2}^{1} $ 

−1551.56 (0.19,40.06 $ ^\circ $ )

3.58 F* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1555.44 (0.16,43.32 $ ^\circ $ )

2.40 200Tl A $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{6}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1570.57 (0.12,56.96 $ ^\circ $ )

0 B $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{5}] $ 

$ \pi s_{1/2}^{-1}\otimes\nu (fp)^{1} $ 

−1569.96 (0.02,1.92 $ ^\circ $ )

0.61 C $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{6}i_{13/2}^{-1}] $ 

$ \pi d_{3/2}^{-1}\otimes\nu i_{13/2}^{-1} $ 

−1568.92 (0.14,53.48 $ ^\circ $ )

1.65 D $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{6}i_{13/2}^{-2}i_{11/2}^{1}] $ 

$ \pi d_{3/2}^{-1}\otimes\nu i_{11/2}^{1} $ 

−1566.90 (0.17,48.94 $ ^\circ $ )

3.67 E $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{6}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1} \otimes\nu i_{13/2}^{-1} $ 

−1566.80 (0.16,51.47 $ ^\circ $ )

3.77 F $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-1}i_{11/2}^{2}] $ 

$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1} $ 

−1564.53 (0.20,47.53 $ ^\circ $ )

6.04 Table 1. The total energies
$E_{\rm tot}$ , excited energies relative to the ground state$E_x({\rm cal.})$ , triaxial deformation parameters β and γ, and their corresponding valence nucleon configurations of minima for states in the configuration-fixed constrained triaxial RMF calculations for the odd-odd nuclei$ ^{192-200} $ Tl. The configurations of the valence proton take reference of 82 nucleons, and those of the valence neutron take reference of 114 nucleons. The suitable states for the appearance of chirality are marked in blue with asterisks.Nuclei States Configuration $ E_{\rm tot} $ 

/MeV$ (\beta, \gamma)^\alpha $ 

$ E_{x}(\rm cal.) $ 

/MeVValence nucleons Unpaired nucleons 193Tl A $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{2}i_{13/2}^{-4}] $ 

$ \pi d_{3/2}^{-1} $ 

−1514.80 (0.18,38.38 $ ^\circ $ )

0 B $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1} $ 

−1514.44 (0.15,37.06 $ ^\circ $ )

0.36 C $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{2}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1} $ 

−1514.35 (0.20,35.54 $ ^\circ $ )

0.45 D $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{2}i_{13/2}^{-4}] $ 

$ \pi s_{1/2}^{-1} $ 

−1513.17 (0.10,0.21 $ ^\circ $ )

1.63 E $ \pi(s_{1/2}^{-1})\otimes\nu [i_{13/2}^{-2}] $ 

$ \pi s_{1/2}^{-1} $ 

−1511.62 (0.05,0.36 $ ^\circ $ )

3.18 F* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu[f_{7/2}^{-2}(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes \nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ 

−1514.27 (0.19,20.64 $ ^\circ $ )

0.53 G* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [f_{7/2}^{-2}(fp)^{3}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes \nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1514.13 (0.20,36.63 $ ^\circ $ )

0.67 H* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{3}i_{13/2}^{-5}] $ 

$ \pi h_{9/2}^{1}\otimes \nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1513.94 (0.15,40.44 $ ^\circ $ )

0.86 I* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu[(fp)^{3}i_{13/2}^{-5}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1513.36 (0.19,20.83 $ ^\circ $ )

1.44 J* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes \nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ 

−1513.13 (0.14,39.64 $ ^\circ $ )

1.67 195Tl A $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1} $ 

−1531.52 (0.15,44.58 $ ^\circ $ )

0 B $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi d_{3/2}^{-1} $ 

−1531.09 (0.18,40.86 $ ^\circ $ )

0.43 C $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1} $ 

−1530.27 (0.20,38.38 $ ^\circ $ )

1.25 D $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi s_{1/2}^{-1} $ 

−1529.80 (0.11,25.12 $ ^\circ $ )

1.73 E $ \pi(s_{1/2}^{-1}) $ 

$ \pi s_{1/2}^{-1} $ 

−1528.19 (0.00,29.86 $ ^\circ $ )

3.34 F $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{2}i_{13/2}^{-2}] $ 

$ \pi s_{1/2}^{-1} $ 

− − − G $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ 

− 1530.95 (0.15,46.12 $ ^\circ $ )

0.57 H $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{5}i_{13/2}^{-5}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1530.92 (0.15,59.90 $ ^\circ $ )

0.60 I* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{3}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1530.73 (0.14,42.94 $ ^\circ $ )

0.79 J* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{3}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1529.96 (0.19,39.70 $ ^\circ $ )

1.56 K* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-4}] $ 

$ \pi h_{9/2}^{1}\otimes\nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ 

−1529.31 (0.19,43.75 $ ^\circ $ )

2.21 L $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{5}i_{13/2}^{-5}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1527.74 (0.19,47.14 $ ^\circ $ )

3.78 197Tl A $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}i_{13/2}^{-2}] $ 

$ \pi h_{9/2}^{1} $ 

−1547.53 (0.13,35.83 $ ^\circ $ )

0 B $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{4}i_{13/2}^{-2}] $ 

$ \pi d_{3/2}^{-1} $ 

−1547.10 (0.15,38.81 $ ^\circ $ )

0.43 C $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{4}i_{13/2}^{-2}] $ 

$ \pi h_{9/2}^{1} $ 

−1546.01 (0.17,38.42 $ ^\circ $ )

1.52 D $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{2}] $ 

$ \pi s_{1/2}^{-1} $ 

−1545.57 (0.09,47.61 $ ^\circ $ )

1.96 E $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{2}] $ 

$ \pi s_{1/2}^{-1} $ 

−1544.92 (0.04,59.83 $ ^\circ $ )

2.61 F* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{5}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1546.73 (0.13,43.18 $ ^\circ $ )

0.8 G* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}i_{13/2}^{-2}] $ 

$ \pi h_{9/2}^{1}\otimes \nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ 

−1546.38 (0.12,40.51 $ ^\circ $ )

1.15 H* $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{3}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes \nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1546.17 (0.12,41.97 $ ^\circ $ )

1.36 I* $ \pi(d_{3/2}^{-2}s_{1/2}^{-2}h_{9/2}^{3})\otimes\nu [(fp)^{3}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes \nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1544.54 (0.17,43.72 $ ^\circ $ )

2.99 J* $ \pi(s_{1/2}^{-2}i_{13/2}^{1})\otimes\nu [(fp)^{3}i_{13/2}^{-1}] $ 

$ \pi i_{13/2}^{1}\otimes \nu [(fp)^{1}i_{13/2}^{-1}] $ 

−1542.89 (0.12,43,29 $ ^\circ $ )

4.64 199Tl A $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{6}i_{13/2}^{-2}] $ 

$ \pi h_{9/2}^{1} $ 

−1562.83 (0.13,50.63 $ ^\circ $ )

0 B $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{4}] $ 

$ \pi h_{9/2}^{1} $ 

−1562.09 (0.11,53.31 $ ^\circ $ )

0.74 C $ \pi(s_{1/2}^{-1})\otimes\nu [(fp)^{4}] $ 

$ \pi s_{1/2}^{-1} $ 

−1561.87 (0.03,0.73 $ ^\circ $ )

0.96 D $ \pi(d_{3/2}^{-1}s_{1/2}^{-2}h_{9/2}^{2})\otimes\nu [(fp)^{6}i_{13/2}^{-2}] $ 

$ \pi d_{3/2}^{-1} $ 

−1561.34 (0.15,48.46 $ ^\circ $ )

1.49 E $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{6}i_{13/1}^{-2}] $ 

$ \pi h_{9/2}^{1} \otimes\nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ 

−1562.51 (0.13,59.96 $ ^\circ $ )

0.32 F $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{5}i_{13/2}^{-1}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1} i_{13/2}^{-1}] $ 

−1562.31 (0.12,51.80 $ ^\circ $ )

0.52 G $ \pi(s_{1/2}^{-2}h_{9/2}^{1})\otimes\nu [(fp)^{7}i_{13/2}^{-3}] $ 

$ \pi h_{9/2}^{1}\otimes\nu [(fp)^{1} i_{13/2}^{-1}] $ 

−1561.58 (0.13,51.24 $ ^\circ $ )

1.25 Table 2. Same as Table 1, but for the odd-mass nuclei
$ ^{193-199} $ T1. -
For 192Tl, as shown in Table 1, the states D* and H* with the proper particle-hole configuration
$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ and triaxial deformation ($ \beta=0.21 $ ,$\gamma=39.84^\circ $ and$\beta= 0.16$ ,$ \gamma=26.17^\circ $ ) are suitable to form the chiral doublet bands. Thus, two sets of chiral doublet bands based on the states D* and H*, namely the MχD bands, are expected in 192Tl.A type of MχD bands, namely four bands with identical configuration, have been reported experimentally in 103Rh [93]. Here, the mechanism of the possible MχD bands in 192Tl is different from that of the four bands in 103Rh. It is worth noting that the states D* and H* have the same unpaired nucleon configuration
$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ but exhibit some differences in the triaxial deformation and valence nucleon configuration (D*:$ \pi (d^{-2}_{3/2}s^{-2}_{1/2}h_{9/2}^{3})\otimes\nu [(fp)^2i_{13/2}^{-5}] $ , H*:$ \pi(s^{-2}_{1/2}h_{9/2}^{1})\otimes\nu (i_{13/2}^{-3}) $ ). This type of MχD in 192Tl is interesting to explore experimentally.For 194Tl, as shown in Table 1, the states C* (
$\beta= 0.14,\gamma=36.81^\circ$ ) and H* ($ \beta=0.17,\gamma=18.80^\circ $ ), related to the same unpaired nucleon configuration$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ , are obtained in the calculations. The present calculations support the existence of chiral doublet bands in 194Tl, and there is a possibility to form the MχD. Ref. [61] suggested that two negative bands form an excellent candidate for chiral doublet bands built on the$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ configuration below the band crossing and the$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-3} $ configuration above the band crossing. To compare with the experimental results above the band crossing, we further perform the particle-hole excitation to the four-quasiparticle configuration. State I* with the triaxial deformation$ (\beta=0.13,\gamma=45.19^\circ) $ and$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-3} $ configuration is obtained in the calculations, which is conducive to the formation of chirality.For 196Tl, as shown in Table 1, the states A* (
$\beta= 0.13,\gamma=34.88^\circ$ ), E*($ \beta=0.18,\gamma=37.26^\circ $ ), and H*($\beta=0.12, \gamma=42.75^\circ$ ) have the same unpaired nucleon configuration$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ . Compared with$ ^{192,194} $ Tl, the hole-like nature of the valence neutron in 196Tl is better, which might be more suitable for the appearance of the chiral doublet bands. Theoretical calculations suggest the MχD in 196Tl combined by six$ \Delta I=1 $ bands based on the$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ configuration.For 198Tl, as shown in Table 1, the states B* (
$\beta= 0.11, \gamma=39.43^\circ$ ) and F* ($ \beta=0.16,\gamma=43.32^\circ $ ), related to the same unpaired nucleon configuration$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ , are obtained in the calculations. The present calculations support the existence of chiral doublet bands in 198Tl, and the phenomenon of MχD is also highly expected. Similar to 194Tl, chiral doublet bands based on the$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ configuration have also been observed experimentally in 198Tl [64, 65], and the two-quasiparticle-plus-triaxial-rotor model calculations show excellent agreement with the experimental data for$ \gamma = 44^\circ $ [65], which is in good agreement with our results.Based on the above discussion for odd-odd thallium isotopes, the calculations suggest the existence of chiral doublet bands based on the configuration
$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ in$ ^{192,194,196,198} $ Tl, as well as the configuration$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1}i_{13/2}^{-1}i_{13/2}^{-1} $ in 194Tl. In experiments, the chiral doublet bands in$ ^{194,198} $ Tl with the configuration$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ have been reported [61, 64, 65], and a rotational band with the same configuration was observed in 192Tl [94, 95] and 196Tl [96], respectively. To study the systematic properties of these rotational bands, the excitation energies and transition probability ratios B(M1)/B(E2) of the main band and its chiral partner band (if it exists) with the$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1} $ configuration in$ ^{192,194,196,198} $ Tl are plotted in Fig. 4 (a-h). As shown in Fig. 4 (a-h), the energy spectra and B(M1)/B(E2) values of the negative-parity band in$ ^{192,196} $ Tl are in accordance with the systematics of the adjacent odd-odd chiral nuclei$ ^{194,198} $ Tl, which also implies the existence of chirality in$ ^{192,196} $ Tl. Furthermore, MχD bands based on the same unpaired nucleon configuration$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ but different triaxial deformation and nucleon occupation are predicted in$ ^{192,194,196,198} $ Tl. It would be interesting to explore these MχD bands experimentally.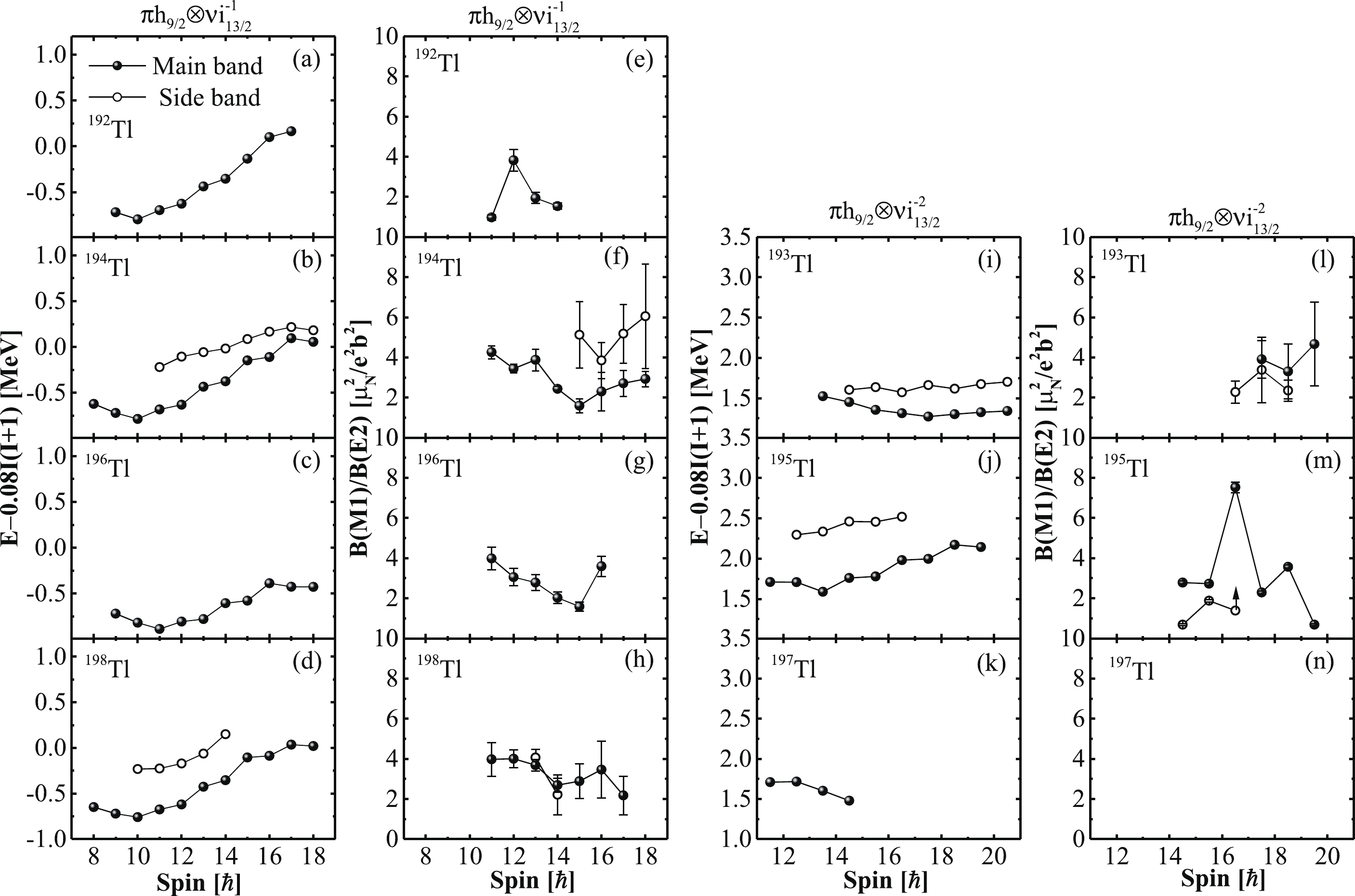
Figure 4. Excitation energies and B(M1)/B(E2) values of the main band and its chiral partner (if it exists) with the
$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1} $ configuration in$ ^{192,194,196,198} $ Tl (a-h) and the$ \pi h_{9/2}^{1}\otimes \nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ configuration in$ ^{193,195,197} $ Tl (i-n). The experimental data have been obtained from Refs. [24, 60, 61, 64, 65, 94–98]. -
For the odd-mass thallium isotopes, the calculation of the adiabatic and configuration-fixed constrained triaxial RMF is similar to that for the odd-odd nucleus, except for performing the particle-hole excitation to three-quasiparticle configurations. Two types of three-quasiparticle chiral configurations can be expected for the odd-mass thallium isotopes: one occurs when a low-
$ j $ fp -shell neutron (which acts as a spectator) is coupled to the neighboring odd-odd chiral configuration; the second is formed by an aligned pair of high-j$ i_{13/2} $ neutron holes, i.e.,$\pi h_{9/2}^1\otimes \nu i_{13/2}^{-1} i_{13/2}^{-1}$ .For 193Tl, as shown in Table 2, states B
$(\beta=0.15,$ $\gamma=37.06^\circ)$ and C ($ \beta=0.20,\gamma=35.54^\circ $ ) have the triaxial deformation and the same unpaired nucleon configuration$ \pi h_{9/2}^{1} $ . We perform the excitation based on states B and C to obtain the states F*, G*, H*, I*, J*, which have prominent triaxial deformation. The configurations are$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1} i_{13/2}^{-1} $ for states F*, J* and$\pi h_{9/2}^{1}\otimes \nu (fp)^1 i_{13/2}^{-1}$ for states G*, H*, I*, which are suitable for the appearance of chirality. Thus, MχD combined by three sets of positive-parity chiral doublet bands and two sets of negative-parity chiral doublet bands are expected to be observed in 193Tl according to the calculations.For 195Tl, similar to 193Tl, states I*, J* with configuration
$ \pi h_{9/2}^{1}\otimes\nu (fp)^1i_{13/2}^{-1} $ , and state K* with configuration$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1}i_{13/2}^{-1} $ are obtained with prominent triaxial deformation, which can possibly form the chiral doublet bands. Thus, MχD with three-quasiparticle configurations combined by two sets of positive-parity chiral doublet bands and one set of negative-parity chiral doublet bands are expected to be observed in 195Tl according to the calculations. Prior to this work, RMF calculations for 195Tl were also performed in Ref. [50]. The deformations and excitation energies for the low lying states A ($ \pi h_{9/2}^{1} $ ), D ($ \pi s_{1/2}^{-1} $ ), and G [$ \pi h_{9/2}^{1}\otimes\nu (i_{13/2}^{-1}i_{13/2}^{-1}) $ ] (corresponding to the A, B, and C states in Ref. [50]) are consistent with the calculated results in Ref. [50]. The present calculation cannot provide the five-quasiparticle states. In addition, chiral doublet bands based on states I*, J* have never been reported experimentally in the nucleus, which is worth exploring further.For 197Tl, similar to
$ ^{193,195} $ Tl, states F*, H*, I* with configuration$ \pi h_{9/2}^{1}\otimes \nu (fp)^1 i_{13/2}^{-1} $ , state G* with configuration$ \pi h_{9/2}^{1}\otimes\nu i_{13/2}^{-1}i_{13/2}^{-1} $ , and state J* with configuration$ \pi i_{13/2}^1\otimes\nu(fp)^1 i_{13/2}^{-1} $ are obtained with prominent triaxial deformation, which can possibly form the chiral doublet bands. Thus, MχD with three-quasiparticle configurations combined by three sets of positive-parity chiral doublet bands and two sets of negative-parity chiral doublet bands are expected to be observed in 197Tl according to the calculations. In addition, a pair of negative-parity rotational bands (B2 and B3 bands in Ref. [97]) were found with the assigned configuration$ \pi i_{13/2}^1\otimes \nu(fp)^1 i_{13/2}^{-1} $ in 197Tl, and whether or not chirality exists in these two bands remains an open question.Based on the above discussion for odd-mass thallium isotopes, the calculations suggest the possible formations of chirality based on the configurations
$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} i_{13/2}^{-1} $ and$ \pi h_{9/2}^{1}\otimes \nu (fp)^1 i_{13/2}^{-1} $ in$ ^{193,195,197} $ Tl, as well as the configuration$ \pi i_{13/2}^{1}\otimes\nu (fp)^{1}i_{13/2}^{-1} $ in 197 Tl. Compared with the calculated results for the odd-odd thallium isotopes, there are more candidate states to form chirality obtained in odd-mass isotopes. In experiments, candidate chiral doublet bands with the configuration$ \pi h_{9/2}^{1}\otimes \nu i_{13/2}^{-1} i_{13/2}^{-1} $ have been reported in 193Tl [60] and 195Tl [24]. A rotational band based on the same configuration in 197Tl has been observed [97]. The excitation energies and B(M1)/B(E2) values of these observed bands are shown in Fig. 4 (i-n). As shown in Fig. 4 (i-n), the energy spectrum of the band in 197Tl is in accordance with the systematics of the adjacent odd-A chiral nuclei$ ^{193,195} $ Tl, but the corresponding B(M1)/B(E2) values are still lacking. Therefore, further experiments are necessary to study the band in 197Tl and search for its chiral partner. Furthermore, the phenomenon of MχD bands based on the above configurations in$ ^{193,195,197} $ Tl should be explored experimentally. -
The chirality in thallium isotopes was investigated using the adiabatic and configuration-fixed constrained triaxial relativistic mean field theory. The calculations suggest that the configuration
$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} $ in odd-odd nuclei$ ^{192,194,196,198} $ Tl, configuration$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1}i_{13/2}^{-1}i_{13/2}^{-1} $ in 194Tl, configurations$ \pi h_{9/2}^1\otimes\nu i_{13/2}^{-1} i_{13/2}^{-1} $ &$\pi h_{9/2}^{1}\otimes \nu (fp)^1 i_{13/2}^{-1}$ in odd-mass nuclei$ ^{193,195,197} $ Tl, and configuration$ \pi i_{13/2}^{1}\otimes\nu (fp)^{1}i_{13/2}^{-1} $ in 197Tl with their triaxial deformations favor the existence of chirality. As the chiral doublet bands in$ ^{193,194,195,198} $ Tl have been reported, the chiral doublet bands in$ ^{192,196,197} $ Tl are expected to be observed experimentally.Furthermore, the possible existence of MχD bands is demonstrated in
$ ^{192,193,194,195,196,197,198} $ Tl. MχD bands based on the same unpaired nucleon configuration but different triaxial deformation and nucleon occupation are predicted. It would be interesting to explore the phenomenon of MχD bands in thallium isotopes experimentally.This paper will motivate an experimental investigation of these nuclei with the possibility to confirm the predicted chirality and MχD in thallium isotopes and facilitate the search for a possible "island of chiral nuclei" in the 190 mass region.
Possible existence of chiral and multiple chiral nuclei in thallium isotopes
- Received Date: 2022-01-07
- Available Online: 2022-07-15
Abstract: The chirality in thallium isotopes is investigated using the adiabatic and configuration-fixed constrained triaxial relativistic mean field theory. Several minima with prominent triaxial deformation and proper configuration, where the chiral doublet bands may appear, are obtained in odd-odd nuclei





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: