-
The investigation of baryon structure is one of the most important issues in hadronic physics and is attracting much attention. Electric (
$G_{\rm E}$ ) and magnetic ($G_{\rm M}$ ) form factors (EMFFs) are fundamental quantities that describe the electromagnetic structure of hadrons [1–4]. A multitude of experimental and theoretical efforts have been made in the past decades. On the one hand, with the planned new and upgraded experimental facilities, the EMFFs of proton in the space-like region can be extracted from$ ep $ scattering [5]. On the other hand, measurements of time-like EMFFs of hadrons can be carried out in the electron-positron annihilation processes, which provide a key to understanding quantum chromodynamic effects in bound states. For example, there is great progress in the study of baryon EMFFs in the time-like region, both on the experimental [6–25] and theoretical [26–45] sides.Very recently, the reaction of
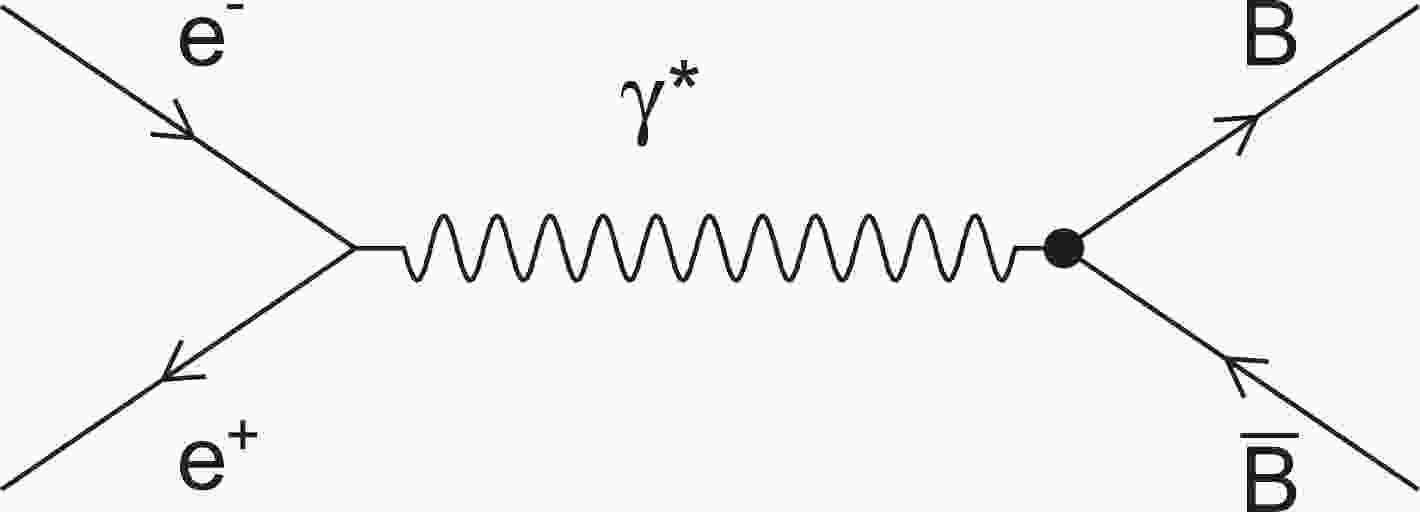
$ e^+e^- \to n\bar{n} $ was measured by the BESIII experiment at centre of mass energies between 2.00 and 3.08 GeV, with very high precision. This precise measurement clarifies that the effective form factors of the neutron are of the same magnitude but smaller than those of the proton. This new result shows that the photon-proton interaction is stronger than the corresponding photon-neutron interaction. Furthermore, an oscillating behavior in the modulus of the effective form factors after the subtraction of a dipole function has been observed for the neutron [46], similar to the case for the proton [43–45].Assuming single-photon exchange (see Fig. 1), the so-called Born cross section of electron–positron annihilation into a baryon–antibaryon pair,
$ e^+ e^- \to B\bar{B} $ with B a spin 1/2 baryon and$ \bar{B} $ an antibaryon, can be expressed in terms of the time-like electric and magnetic form factors$G_{\rm E}$ and$G_{\rm M}$ as [34]①$ \sigma_{\rm B} (s) = \frac{4 \pi \alpha^2 \beta}{3 s^2} \left( s \left|G_{\rm M}\left( s \right)\right|^{2} + 2M^2_{\rm B} \left|G_{\rm E}\left( s \right)\right|^{2}\right), $

(1) where
$ \alpha = e^2/(4\pi) = 1/137.036 $ is the fine-structure constant,$\beta = \sqrt{1-4 M_{\rm B}^{2}/s}$ is a phase-space factor,$M_{\rm B}$ is the baryon mass, and s is the invariant mass square of the$ e^+ e^- $ system. In the space-like region,$G_{\rm E}$ and$G_{\rm M}$ are real, while in the time-like region, they are complex.The measurement of the total cross section in Eq. (1) at a fixed energy allows for determination of the combination of
$|G_{\rm E}|^2$ and$|G_{\rm M}|^2$ . Instead of a separation between$G_{\rm E}$ and$G_{\rm M}$ , one can easily obtain the effective form factor$ G_{\rm eff}(s) $ from the total cross section of the$ e^+ e^- $ annihilation process [19, 21]. This is defined as$ \begin{aligned}[b] |G_{\rm{eff}}\left( s \right)| =& \sqrt{\frac{\sigma_{\rm B}}{[1+1/(2\tau)][4\pi\alpha^2\beta/(3s)]}} \\ =& \sqrt{\frac{2 \tau\left|G_{\rm M}\left(s\right)\right|^{2}+\left|G_{\rm E}\left(s\right)\right|^{2}}{1+2 \tau}}, \end{aligned} $

(2) where
$\tau = s/(4 M^2_{\rm B})$ . The effective form factor$ |G_{\rm eff}(s)|^2 $ is a linear combination of$|G_{\rm E}|^2$ and$|G_{\rm M}|^2$ , and it indicates how much the experimental$ e^+e^- \to B \bar{B} $ cross section differs from a point-like baryon B. Therefore, the effective form factor$ G_{\rm eff}(s) $ can be determined from a measurement of the total cross section of the$ e^+ e^- $ annihilation process. The values of$ |G_{\rm eff}(s)| $ depend, in principle, on the kinematics where the measurement was performed. The effective form factor also describes the coupling constants for the elementary process$ e^+e^- $ to quark–antiquark pairs.In general, the experimental data on the effective form factor
$ |G_{{\rm eff}}(s)| $ can be well reproduced by a dipole function$G_{\rm D}(s)$ , which has a decreasing behavior as a function of s. Its form is commonly written as [44–47]$ G_{\rm D}(s)=\frac{c_0} {(1-\gamma s)^2 }, $

(3) where
$ c_0 $ and γ are constants to be determined from the experimental data. The dipole form of Eq. (3) is extended from the intrinsic nucleon form factor$ g(t) $ in the space-like region as introduced in Ref. [48]. The intrinsic form factor describes a direct coupling of the proton to the virtual photon with squared four-momentum transfer t. This dipole form was obtained from the best fit to the electromagnetic form factors of proton in the space-like region (see also Refs. [49–51] for more details).The oscillating component of the effective form factor can be easily fitted by the following equation:
$ G_{\rm {osc}}(s) = \frac{c_0} {(1-\gamma s)^2 } A \cos (C \sqrt{s} + D), $

(4) where the normalization A, the frequency C, and the phase D are constants to be determined from the experimental measurements. Then, the total effective form factor
$ G_{\rm eff} $ is:$ \begin{aligned}[b] G_{\rm {eff}}(s) =& G_{\rm D} (s) + G_{\rm {osc }}(s) \\ =& \frac{c_0} {(1-\gamma s)^2 } \left( 1 + A \cos (C \sqrt{s} + D) \right ) . \end{aligned} $

(5) It is worth mentioning that we take the oscillating component as a function of the invariant mass
$ \sqrt{s} $ rather than the relative momentum p as used in Refs. [44–47], where p is a function of the invariant mass$ \sqrt{s} : p = \sqrt{s(\tau -1)} $ . Indeed, to investigate the effects of the final state interactions of the$ B\bar{B} $ pair at the reaction threshold in the$ e^+e^- \to B\bar{B} $ data, it is more convenient to introduce$ G_{\rm osc} $ as directly related to the relative momentum of the$ B\bar{B} $ pair. In Refs. [44, 45], it has been suggested that the rescattering processes for the final production of the$ B\bar{B} $ pair may contribute to the oscillations. However, the rescattering mechanism of the final$ B\bar{B} $ pair is still unknown [44, 52, 53]. Here we restrict ourselves to a discussion of combined analysis that include data on the effective form factors of these neutral particles with spin$ 1/2 $ . In the following we will show that the oscillating behavior can be also seen when the$ G_{\rm osc} $ was plotted as a function of$ \sqrt{s} $ . Furthermore, the natural exponential reduced function used in Refs. [44–47] is also replaced by the dipole function, which is the same as for the main component of the effective form factor. By this method, the number of free parameters is reduced.Although there is no fundamental explanation for the oscillating behavior of the nucleon effective form factors, modelling the joint information from all the current experimental data on the effective form factors of baryons may bring a new view of the reaction mechanism for the formation of baryons. Along these lines, in this work, we performed a combined analysis of the effective form factors of these neutral particles with spin 1/2: neutron, Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ . It is found that the effective form factors of these hyperons show a universal phenomenon of oscillating behavior, similar to the observations for proton and neutron. Further experimental and theoretical investigations of such behavior may open a new window on the electromagnetic structure of Λ,$ \Sigma^0 $ , and$ \Xi^0 $ hyperons. -
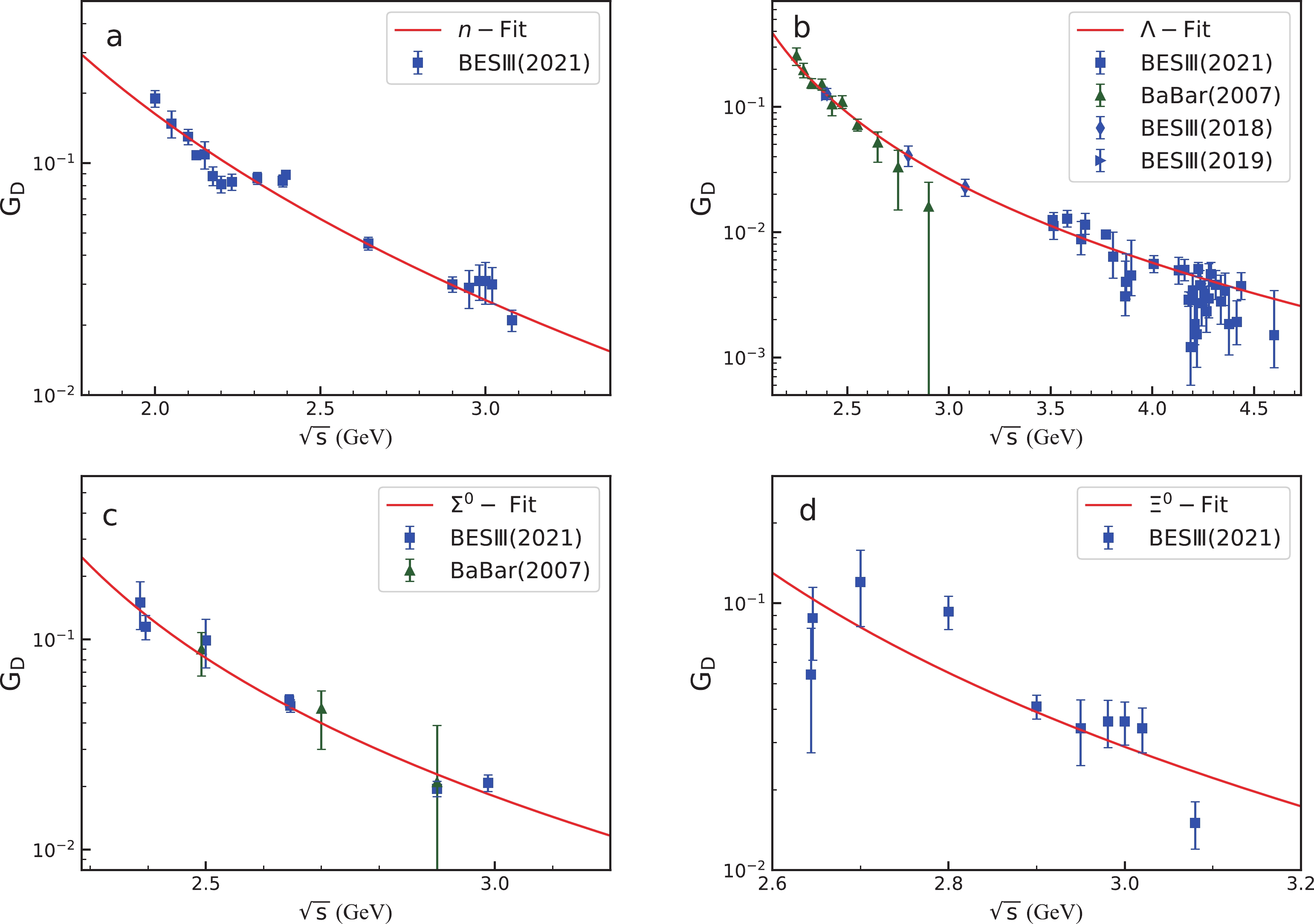
Firstly, we perform two parameter
$ \chi^2 $ fits (for$ c_0 $ and γ) with the dominant dipole component$G_{\rm D}(s)$ as in Eq. (3) to the experimental data on the effective form factors of the neutron, Λ,$ \Sigma^0 $ , and$ \Xi^0 $ . The fitted parameters and the corresponding$ \chi^2/{\rm dof} $ are shown in Table 1.Parameter n Λ $ \Sigma^0 $ 

$ \Xi^0 $ 

γ 1.41 (fixed) 0.34 ± 0.08 0.26 ± 0.01 0.21 ± 0.02 $ c_0 $ 

3.48 ± 0.06 0.11 ± 0.01 0.033 ± 0.007 0.023 ± 0.008 χ2/dof 4.3 2.4 1.1 3.0 Table 1. Fitted parameters for the effective form factors with the dipole function shown in Eq. (3). The unit of γ is
$ {\rm GeV}^{-2} $ .For the neutron, we take the value of
$ \gamma = \dfrac{1}{0.71 {\rm GeV}^{2}} $ as in Refs. [46, 47]. This value is also used for the proton. If we make$ c_0 $ and γ free parameters for the case of neutron, there is always another solution from the$ \chi^2 $ fit, which is:$ c_0 = 96.6 $ and$ \gamma = 6.6 $ $ {\rm GeV}^{-2} $ , where both parameters have huge errors. In fact, the line shape of neutron$ G_{\rm eff} $ is trivial and there are many solutions to describe it. Hence, it is also found that$ c_0 $ and γ are strongly correlated.In Fig. 2, we show the fitted results for the effective form factors of the neutron, Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ with a dipole function$G_{\rm D}(s)$ as in Eq. (3). One can see that the effective form factors can be fairly well reproduced using the dipole function.② Especially, the data of$ \Sigma^0 $ are in agreement with a dipole function, with a goodness of fit$ \chi^2/{\rm dof} = 1.1 $ .In addition, from the fitted values of γ, it is found that the effective form factors of Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ hyperons reduce more quickly than those of the proton and neutron, when$ \sqrt{s} $ is growing. For Λ, from the invariant mass$ \sqrt{s} = 2.3 $ GeV to 3.3 GeV,$G_{\rm D}(s)$ reduces from 0.172 to 0.015, while for the case of the neutron, from$ \sqrt{s} = 2.0 $ GeV to 3.0 GeV, its effective form factor reduces from the value of 0.162 to 0.025. -
After subtracting the main dipole component from the effective form factor, then one obtains the oscillating component
$ G_{\rm {osc }}(s) $ . We have performed three parameter$ \chi^2 $ fits (for A, C, and D) with the oscillating component$ G_{\rm osc}(s) $ as in Eq. (4) for the neutron, Λ,$ \Sigma^0 $ , and$ \Xi^0 $ . The fitted parameters and the corresponding$ \chi^2/{\rm dof} $ are shown in Table 2. Since the uncertainties of these experimental data are large, the fitted parameters have big uncertainties. In addition, the parameters C and D are strongly correlated.Parameter n Λ $ \Sigma^0 $ 

$ \Xi^0 $ 

$ A (10^{-2}) $ 

$ 17.6 \pm 2.7 $ 

17.6 (fixed) $ 19.9 \pm 10.2 $ 

$ 23.2 \pm 9.6 $ 

C $ 12.2 \pm 0.6 $ 

12.2 (fixed) $ 11.9 \pm 1.1 $ 

$ 10.6 \pm 2.2 $ 

D $ 1.66 \pm 1.41 $ 

$ 2.37 \pm 1.88 $ 

$ 0.99 \pm 3.13 $ 

$ 1.34 \pm 6.39 $ 

$ \chi^2/{\rm dof} $ 

1.4 0.6 0.4 1.9 Table 2. Fitted parameters for the oscillating component of the effective form factors of the neutron, Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ . The unit of C is$ {\rm GeV}^{-1} $ .With the central values of these fitted parameters shown in Table 2, we show in Fig. 3 the numerical results for the oscillating component of the effective form factors of the neutron, Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ . One can see that the oscillating component can be fairly well described by a function$ G_{\rm osc}(s) $ as in Eq. (4). It is worth mentioning that the current experimental data with large errors do not allow us to obtain unique values for the model parameters, which are introduced in Eq. (4). The fit is quite sensitive to the choice of initial values of parameters.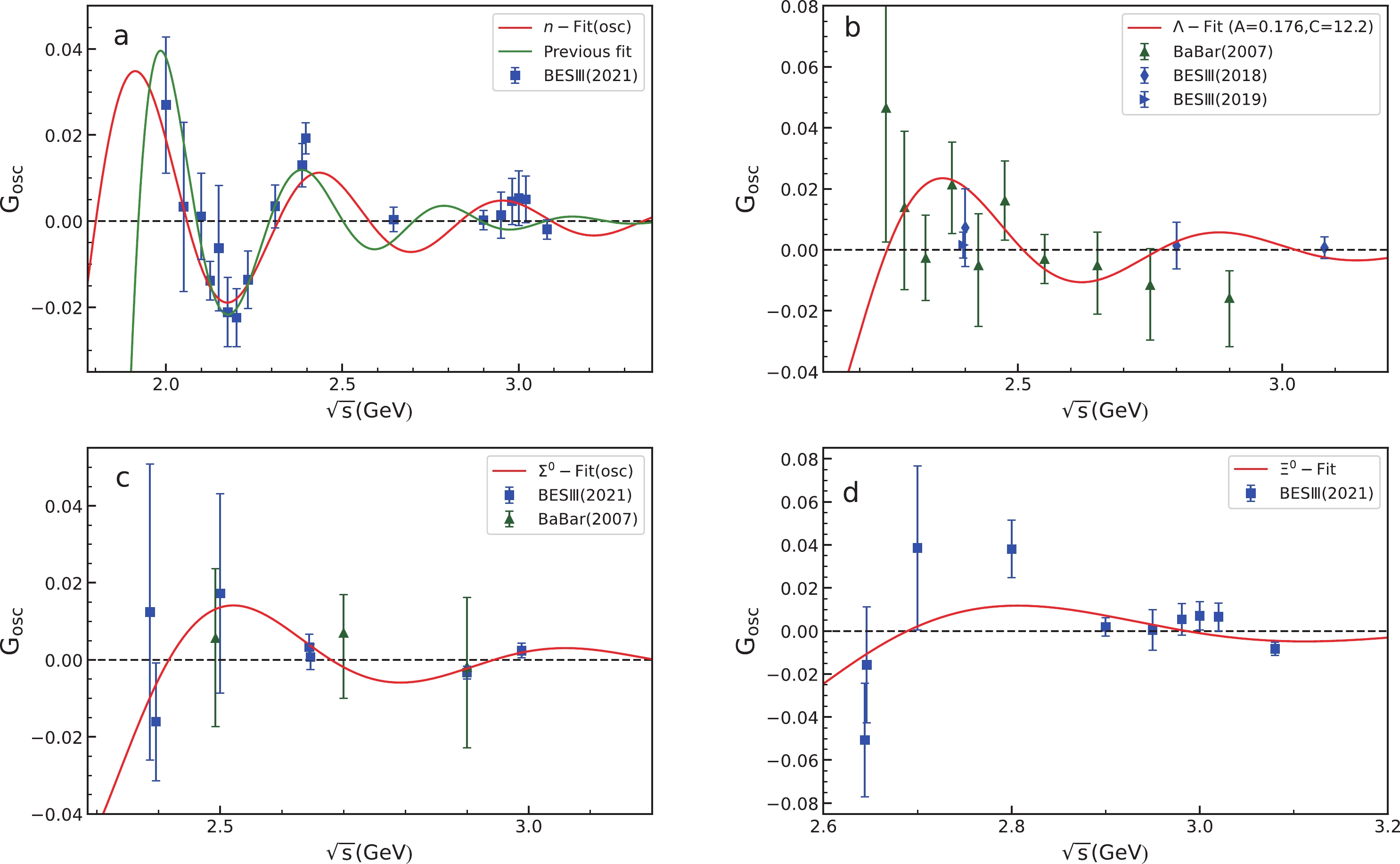
Figure 3. (color online) Fitting results of the oscillating component of the neutron (a), Λ (b),
$ \Sigma^0 $ (c), and$ \Xi^0 $ (d) effective form factors.For Λ, we have fixed
$ A=0.176 $ and$ C=12.2 \; {\rm GeV}^{-1} $ , which are same as the values obtained from the fit for neutron. If we make A and C for Λ free parameters, we can also get a good fit with$ \chi^2/{\rm dof} = 0.6 $ . The fitted parameters are:$ A= 9.0 \pm 8.8 $ ,$ C=4.0 \pm 2.3 \; {\rm GeV}^{-1} $ , and$ D = 3.2 \pm 5.6 $ . It is found that these fitted parameters have very large errors. Besides, the fitted value of frequency C is very small, compared with those ones for the neutron,$ \Sigma^0 $ , and$ \Xi^0 $ .For
$ \Sigma^0 $ and$ \Xi^0 $ , if the values of A and C were fixed at the values for the neutron, one can also get good fits with$ \chi^2/{\rm dof} = 0.3 $ and 1.4, respectively. The corresponding fitted values for parameter D are$ 0.24 \pm 0.23 $ and$ 1.35 \pm 0.36 $ for$ \Sigma^0 $ and$ \Xi^0 $ , respectively.In Fig. 3 (a), for comparison, we show also the fitted results of Refs. [46, 47] by the green curve with 4-parameter function
$ G_{\rm osc} = Ae^{-Bp}{\rm cos}(Cp+D) $ and$ A=0.08 $ ,$ B=1.01 {\rm GeV}^{-1} $ ,$ C=5.28 \;{\rm GeV}^{-1} $ , and$ D=-3.77 $ . The two fitted results are very similar between$ \sqrt{s} =2.0 $ and 2.5 GeV. But they are significantly different beyond$ \sqrt{s}=2.5 $ GeV. It is worth mentioning that$ \chi^2/{\rm dof} = 1.4 $ is a little larger than the value 0.9 obtained in Refs. [46, 47]. It is expected that more precise data in future can be used to verify these model calculations.From Figs. 3 (b), (c), and (d) it is found that the data for Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ have larger errors in the threshold region. In our fit for the case of$ \Sigma^0 $ , the first datum was not considered. It is expected that future more precise experimental measurements will check the oscillating behavior of the effective form factor of the Λ,$ \Sigma^0 $ , and$ \Xi^0 $ hyperons. Moreover, the process of hyperon–antihyperon pair production in the electron–position annihilation can be also used to study the polarizations of hyperons.The fitted parameters shown in Table 2 indicate an interesting oscillating behavior with very similar normalization A and frequency C for these neutral baryons. As discussed above, the oscillating data on the neutron, Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ can be fairly well described with the same values of parameters A and C. In Fig. 4, we put all the oscillating data for the neutron, Λ,$ \Sigma^0 $ , and$ \Xi^0 $ together. The red solid line stands for the results with these fitted parameters of neutron data. Because of large errors in the experimental data for Λ,$ \Sigma^0 $ , and$ \Xi^0 $ hyperons, one can see that the red line is not in disagreement with these current data on Λ,$ \Sigma^0 $ , and$ \Xi^0 $ within uncertainties. No firm conclusions can yet be made, however the behavior may indicate unexplored intrinsic dynamics. For example, vector mesons with mass around or above 2 GeV should contribute to this oscillating behavior (more discussions can be found in Refs. [35, 37]). -
In summary, we have considered the available experimental data on the effective form factors of several neutral baryons, namely the neutron, Λ,
$ \Sigma^0 $ , and$ \Xi^0 $ , that were measured by BaBar and BESIII collaborations. A general fit to these data has been performed with the aim to investigate the oscillating behavior of the effective form factors. It is found that the experimental data for the neutron, Λ,$ \Sigma^0 $ , and$ \Xi^0 $ are in fair agreement with a simple dipole function. However, our analysis does show evidence for the oscillating features in the effective form factors of the neutron, Λ, and$ \Sigma^0 $ , which can be tested by future precise data from BESIII [54–56]. Further improvements both in the precision of the experimental data on the effective form factors as well as the$ \sqrt{s} $ range will further improve our understanding of the inner electromagnetic structure and dynamics of these neutral baryons. -
We thank Profs. De-Xu Lin and Xiong-Fei Wang for useful discussions.
Electromagnetic form factors of neutron and neutral hyperons in the oscillating point of view
- Received Date: 2022-02-04
- Available Online: 2022-07-15
Abstract: Based on the recent precise measurements by the BESIII collaboration for electron–positron annihilation into a neutron and antineutron pair, the effective form factors of the neutron were determined in the time-like region, and it was found that the effective form factors of the neutron are smaller than those of the proton. The effective form factors of the neutron show a periodic behaviour, similar to those of the proton. Here, a comparative analysis for Λ,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: