-
In the conventional quark model mesons are made of quark-anti-quark (
$ q\bar{q} $ ) and baryons are made of three quarks ($ qqq $ ). Such a simple picture has achieved significant successes in the description of hadron spectra based on the constituent quark degrees of freedom. Meanwhile, as the fundamental theory for strong interactions, QCD predicts the existence of hadrons with more sophisticated structures, namely, exotic hadrons. These states, of which the structures are beyond the conventional quark model, have been a crucial probe for the non-perturbative phenomena of QCD. Among all the exotic candidates, hadrons with such quantum numbers that cannot be accommodated by the conventional quark model, would serve as a "smoking gun" for the existence of exotic hadrons. In particular, "hybrid", which contains the explicit excitations of the constituent-like gluonic degrees of freedom, can access the exotic quantum numbers of$ J^{PC}=1^{-+} $ as the lowest eigenstates. Its study has always garnered considerable attention from both experiments and theory.In Refs. [1, 2], the BESIII Collaboration reports the first observation of the
$ 1^{-+} $ isoscalar hybrid candidate$ \eta_1(1855) $ in the partial wave analysis of$ J/\psi\to \gamma \eta_1(1855) $ $ \to \gamma\eta\eta' $ . Its mass and width are$ (1855\pm 9^{+6}_{-1}) $ MeV and$ (188\pm 18^{+3}_{-8}) $ MeV, respectively. This progress may provide a great opportunity for a better understanding of these mysterious species of the QCD-predicted exotic states.Historically, evidences for the
$ 1^{-+} $ hybrid were found by various experiments [3–8]; in addition, two light hybrid candidates,$ \pi_1(1400) $ and$ \pi_1(1600) $ , were reported. However, owing to the limited statistics, their existences were far from broadly accepted. A comprehensive review of the early experimental results can be found in Refs. [9, 10]. Strong indication of the$ 1^{-+} $ hybrid$ \pi_1(1600) $ is obtained from the COMPASS Collaboration based on their partial wave analysis (PWA) results for$ \pi^- p\to p \pi^+\pi^-\pi^- $ [11–14]. In a recent detailed analysis [15] by COMPASS, it shows that the$ \pi_1(1600) $ signal cannot be accounted for by the Deck effect [16]. A reanalysis of the COMPASS data with the coupled-channel approach also supports that the$ \pi_1(1600) $ signal should be originated from a pole structure in the scattering amplitude [17]. These results have provided strong evidences for$ \pi_1(1600) $ as a well-established$ 1^{-+} $ hybrid candidate. In contrast, the signals for$ \pi_1(1400) $ are ultimately vague. According to the analysis of Ref. [17], there is no need for the$ \pi_1(1400) $ to be present in the$ \rho\pi $ channel.Phenomenological studies on the
$ 1^{-+} $ hybrid state can be found in the literature. By treating the gluonic excitation as an explicit constituent degree of freedom, phenomenological models were constructed to understand the exotic hadron spectrum or describe the mechanisms for their productions and decays [18, 19]. Among all these efforts, the flux tube model has achieved significant success in accommodating the broadly adopted quark pair creation (QPC) model for the strong decays of conventional hadrons and gluonic excitations of QCD exotics [20–23]. Calculations in the framework of QCD sum rules also provide interesting results on the properties of the light hybrid$ \pi_1 $ state [24, 25]. In Ref. [26], the decay properties are studied for$ \pi_1 $ and its non-strange isoscalar partner. In Ref. [27], it is investigated that an isoscalar with$ I^G(J^{PC})=0^+(1^{-+}) $ may be formed as a bound state of$ \eta \bar{K}K^* $ . However, the mass is much lower than$ \eta_1(1855) $ .There is no doubt that lattice QCD (LQCD) simulations should play a crucial role in guiding the search for the hybrid states. In Ref. [28], the first systematic LQCD study on the excited isoscalar meson spectra was presented. It is interesting to observe the emergence of the mixing patterns between the SU(3) flavor singlet and octet such as the η and
$ \eta' $ mixing. In the$ 1^{-+} $ hybrid sector, some hints for the mixing between the non-strange and strange configurations are found. Meanwhile, its prediction of the isoscalar$ 1^{-+} $ hybrid spectrum indicates relatively higher masses than the light axial vector mesons. It implies an unusual behavior of the excitations of the gluonic degrees of freedom in comparison with the orbital excitations within conventional$ q\bar{q} $ systems.In light of the discovery of
$ \eta_1(1855) $ by BESIII [1, 2] and the LQCD simulations [28, 29], we propose a nonet scheme for the$ 1^{-(+)} $ hybrid states. In this scheme,$ \pi_1(1600) $ is the$ I=1 $ state with the lowest mass, and$ \eta_1(1855) $ is identified as one of the$ I=0 $ multiplets. The strange$ I=1/2 $ partner is assigned to$ K^*(1680) $ , which is the only strange vector meson found in the vicinity of the$ 1.6\sim 1.9 $ GeV mass region. Although the strange hybrid does not have a fixed charge conjugate parity, it cannot be easily distinguished from the conventional$ q\bar{q} $ vector meson; hence, there is no strong reason to suggest that such an exotic object should not exist. Considering the flavor-blind property of QCD, the strange hybrid of$ q\bar{s}\tilde{g} $ should at least share similar dynamics as the$ I=1 $ partner$ \pi_1(1600) $ . In Ref. [28], the mass splitting between the flavor singlet and octet is determined to be significant. This is attributed to the important effects from the quark annihilations in the$ I=0 $ sector.As follows, we first analyse the mixing between
$ \eta_1(1855) $ and its isoscalar partner, and the mass relationships among the$ 1^{-(+)} $ hybrid nonet. Two schemes, in which$ \eta_1(1855) $ is assigned to be either the higher or lower mass state in the$ I=0 $ sector, are explored based on the flux tube model picture. Phenomenological consequences will be discussed in their productions and decays in several typical processes. A brief summary will be given in the end. -
On the SU(3) flavor basis, the light hybrid mesons are described by a pair of
$ q\bar{q} $ associated by gluonic quasiparticle excitations. Taking the flux tube model picture, the$ q\bar{q} $ inside hybrid mesons are separated static color sources and are connected by the gluonic flux tube, to form an overall color singlet. The transverse oscillations of the flux tube that manifest the explicit effective gluonic degrees of freedom, will lead to the energy spectrum of the hybrid mesons. As studied in the literature, the lowest energy flux tube motion has$ J_g^{PC}=1^{+-} $ . Namely, the lightest hybrid multiplet can be formed by the relative S-wave coupling between a gluonic lump of$ J_g^{PC}=1^{+-} $ and an S-wave$ q\bar{q} $ pair. With the total gluon spin$ J_g^{PC}=1^{+-} $ , the lowest hybrid multiplets can be obtained:$ (0, \ 1, \ 2)^{-+}, \ 1^{--} $ [29, 30]. Alternatively, in the constituent gluon picture, the lowest energy flux tube excitation can be described by the motion of quasigluon in a P wave, with respect to the S-wave$ q\bar{q} $ .The gluonic excitations additive to the S-wave constituent
$ q\bar{q} $ configuration suggest that for each S-wave$ q\bar{q} $ pair, there should exist an SU(3) flavor nonet as the eigenstates of the corresponding Hamiltonian. For the same coupling mode involving the gluonic lump, these states can be related to each other by the Gell-Mann-Okubo mass relationship similar to that for the ground states in the$ q\bar{q} $ scenario. This conjecture may have a caveat when the strange multiplets are included. Because the charged and strange states do not have the fixed C parity, this may raise the question whether a nonet scheme is feasible. Note that signals for charged$ \pi_1(1600) $ have been seen in the decay channels of$ \rho^0\pi^- $ [11] and$ \eta'\pi^- $ [12, 13]. Similar dynamics should appear in the strange sector and a nonet structure among the$ 1^{-(+)} $ multiplets should provide optimal guidance for a better understanding of the underlying dynamics.Taking the
$ 1^{-+} $ hybrid as an example, it should contain flavor multiplets as follows:$ \pi_1^+, \ \pi_1^-, \ \pi_1^0 : u\bar{d}\tilde{g}, \ d\bar{u}\tilde{g}, \ \frac{1}{\sqrt{2}}(u\bar{u}-d\bar{d})\tilde{g} \ , $

(1) $ \eta_{1}^{(8)} : \frac{1}{\sqrt{6}}(u\bar{u}+d\bar{d}-2s\bar{s})\tilde{g} \ , $

(2) $ \eta_{1}^{(1)} : \frac{1}{\sqrt{3}}(u\bar{u}+d\bar{d}+s\bar{s})\tilde{g} \ , $

(3) $ K^{*+}, \ K^{*0}, \ K^{*-}, \ \bar{K}^{*0} : u\bar{s}\tilde{g}, \ d\bar{s}\tilde{g}, \ s\bar{u}\tilde{g}, \ s\bar{d}\tilde{g} \ , $

(4) where
$ \tilde{g} $ represents the gluonic lump with$ J_g^{PC}=1^{+-} $ . For the flavor octet$ \eta_{1}^{(8)} $ and singlet$ \eta_{1}^{(1)} $ with isospin$ I=0 $ , they may mix with each other to form the corresponding physical states similar to the familiar$ \eta-\eta' $ mixing.Considering the mixing between the hybrid flavor singlet and octet, the physical states can be expressed as
$ \begin{aligned}[b]\left( {\begin{array}{*{20}{c}} {{\eta _{1{\rm L}}}}\\ {{\eta _{1{\rm H}}}} \end{array}} \right) =& \left( {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\eta _1^{(8)}}\\ {\eta _1^{(1)}} \end{array}} \right)\\ =& \left( {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }\\ {\sin \alpha }&{\cos \alpha } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {n\bar n\tilde g}\\ {s\bar s\tilde g} \end{array}} \right), \end{aligned}$

(5) where θ is the mixing angle between the flavor octet and singlet, and α is the mixing angle defined on the flavor basis
$ n\bar{n}\tilde{g} $ (with$ n\bar{n}\equiv (u\bar{u}+d\bar{d})/\sqrt{2} $ ) and$ s\bar{s}\tilde{g} $ .The Gell-Mann-Okubo relationship can provide a constraint on the mixing angle θ via the following equation:
$ \tan\theta = \frac{4m_{K^*}-m_{\pi_1}-3m_{\eta_{1L}}}{2\sqrt{2}(m_{\pi_1}-m_{K^*})} \ , $

(6) where
$ \eta_{1{\rm L}} $ is the lower mass state in Eq. (5) and the sign of θ can be determined here. We note that the same relationship is also satisfied for the quadratic masses. The Gell-Mann-Okubo relationship also leads to the following mass relation,$ \begin{aligned}[b]&(m_{\eta_{1{\rm H}}}+m_{\eta_{1{\rm L}}})(4m_{K^*}-m_{\pi_1})-3m_{\eta_{1{\rm H}}}m_{\eta_{1{\rm L}}}\\ =& 8m_{K^*}^2-8m_{K^*}m_{\pi_1}+3m_{\pi_1}^2 \ , \end{aligned} $

(7) which is symmetric for
$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ , although it is the lower mass state$ \eta_{1{\rm L}} $ defined in Eq. (5) to appear in Eq. (6). With the masses of$ \pi_1(1600) $ and$ \eta_1(1855) $ as the input for Eqs. (6) and (7), we are still unable to determine these three quantities, i.e. θ,$ m_{\eta_{1{\rm H}}}/m_{\eta_{1{\rm L}}} $ and$ m_{K^*} $ . In addition, it is unclear whether$ \eta_1(1855) $ is the lower or higher mass state in Eq. (5). However, we will later demonstrate that the$ \eta\eta' $ channel is informative to impose a constraint on the determination of the$ 1^{-(+)} $ nonet. -
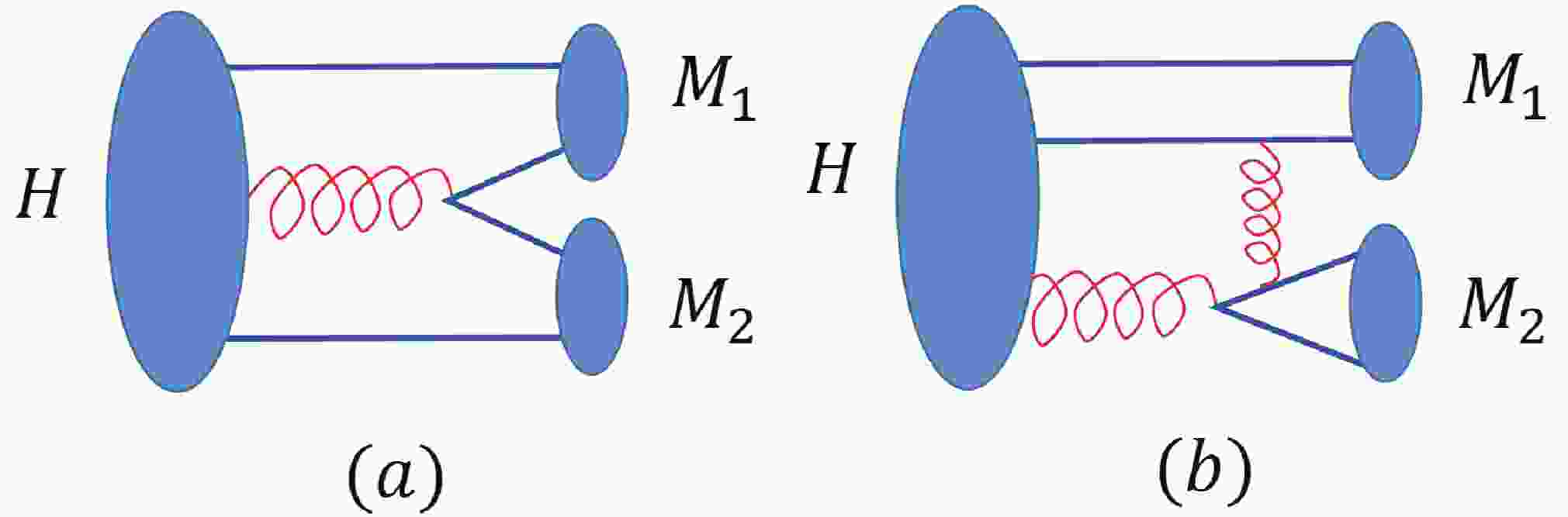
The flavor-blindness of the strong interactions also allows us to relate the SU(3) decay channels together [31–34]. Considering the two-body decay of
$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ into the pseudoscalar meson pair$ PP' $ ①, two independent transition mechanisms can be identified, as illustrated in Fig. 1 (a) and (b). The transition of Fig. 1 (a) represents the flux tube string breaking with the quark pair creation. It is similar to the decay of a conventional$ q\bar{q} $ state into two mesons using the quark pair creation (QPC) mechanism. In the flux tube scenario, it corresponds to the flux excitation mode along the displacement between the quark and anti-quark, for which the potential is denoted as$ \hat{V}_{\rm L} $ . The transition of Fig. 1 (b) corresponds to the flux excitation mode transversal to the displacement between the quark and anti-quark. The quark pair created from this mode will recoil the initial color-octet$ q\bar{q} $ via the transverse flux motion. For a conventional$ q\bar{q} $ decay via the$ ^3P_0 $ QPC mechanism, the kinematic regime as Fig. 1 (b) will be relatively suppressed with respect to Fig. 1 (a). In such a case, in order to balance the color, an additional relatively-hard gluon will be exchanged between the recoiled$ q\bar{q} $ and the created$ q\bar{q} $ . In contrast, such a transition in the hybrid decay can naturally occur via the transverse mode of the flux tube oscillations [35]. Namely, the created$ q\bar{q} $ can easily obtain the color balanced by soft gluon exchanges, which can be absorbed into the effective potential without suppression. Such a transition through the transverse mode of the flux tube motions can be parametrized by the effective potential$ \hat{V}_{\rm T} $ .The transition amplitude for a
$ 1^{-+} $ hybrid of$ q\bar{q}\tilde{g} $ decaying into two pseudoscalar mesons can then be expressed as$ {\cal M}_a = \langle (q_1\bar{q}_4)_{M_1}(q_3\bar{q}_2)_{M_2}|\hat{V}_{\rm L}|q_1\bar{q}_2\tilde{g}\rangle\equiv g_1 |{\boldsymbol k}| \ , $

(8) and
$ {\cal M}_b = \langle (q_1\bar{q}_2)_{M_1}(q_3\bar{q}_4)_{M_2}|\hat{V}_{\rm T}|q_1\bar{q}_2\tilde{g}\rangle\equiv g_2 |{\boldsymbol k}| \ , $

(9) for these two decay modes, respectively. In the above two equations,
$ {\boldsymbol k} $ denotes the three-vector momentum of the final-state meson in the c.m. frame of the hybrid, while the quarks (anti-quarks) represent the non-strange quarks (anti-quarks). Note that the QPC only contributes to a flavor singlet$ \tilde{g}\to (u\bar{u}+d\bar{d}+s\bar{s})/\sqrt{3} $ . We mention that when the$ s\bar{s} $ pair is created, an SU(3) flavor symmetry breaking parameter will be included. Furthermore, in the above two amplitudes, the interchanges of the final-state hadron indices are implied.This parametrization leads to a connection among the couplings of an initial hybrid state to different SU(3) channels, and they are collected in Table 1. Interesting features with the hybrid nonet decays can be learned as follows:
Processes Couplings $ \pi_1^0\to \eta\pi^0 $ 

$ \dfrac{1}{\sqrt{2}}(g_1+g_2)\cos\alpha_P-R g_2\sin\alpha_P $ 

$ \pi_1^0\to \eta'\pi^0 $ 

$ \dfrac{1}{\sqrt{2}}(g_1+g_2)\sin\alpha_P+R g_2\cos\alpha_P $ 

$ \pi_1^+\to\eta\pi^+ $ 

$ \sqrt{2}(g_1+g_2)\cos\alpha_P-R g_2\sin\alpha_P $ 

$ \pi_1^+\to\eta'\pi^+ $ 

$ \sqrt{2}(g_1+g_2)\sin\alpha_P+R g_2\cos\alpha_P $ 

$\eta_{\rm 1L}\to \eta\eta'$ 

$ \dfrac{1}{2}(g_1+g_2)\sin 2\alpha_P(\cos\alpha+R\sin\alpha)+g_2\cos 2\alpha_P(R\cos\alpha-\sin\alpha) $ 

$\eta_{\rm 1H}\to \eta\eta'$ 

$ \dfrac{1}{2}(g_1+g_2)\sin 2\alpha_P(\sin\alpha-R\cos\alpha)+g_2\cos 2\alpha_P(R\sin\alpha+\cos\alpha) $ 

$ K^{*+}\to K^+\pi^0 $ 

$ \dfrac{1}{\sqrt{2}} g_1 $ 

$ K^{*+}\to K^0\pi^+ $ 

$ g_1 $ 

$ K^{*+}\to K^+\eta $ 

$ g_1\left(\dfrac{1}{\sqrt{2}}\cos\alpha_P- R\sin\alpha_P\right) + g_2(\sqrt{2}\cos\alpha_P- R\sin\alpha_P) $ 

$ K^{*+}\to K^+\eta' $ 

$ g_1\left(\dfrac{1}{\sqrt{2}}\sin\alpha_P+ R\cos\alpha_P\right) + g_2(\sqrt{2}\sin\alpha_P+ R\cos\alpha_P) $ 

Table 1. Coupling constants for the
$ 1^{-(+)} $ hybrid nonet decays into pseudoscalar meson pairs. The couplings for the negative charge states are implied. The SU(3) flavor symmetry breaking parameter R is also included.● It is rather clear that if the final states do not contain isoscalar mesons, the transitions will occur via the string breaking potential
$ \hat{V}_{\rm L} $ along the displacement between the quark and anti-quark. Namely, the transitions are similar to the conventional$ ^3P_0 $ process. For$ K^* $ decays into$ K\pi $ , it will be difficult to distinguish them from the conventional$ q\bar{q} $ vector mesons.● Regarding the
$ \pi_1 $ and$ K^* $ decays into η or$ \eta' $ plus a$ I\neq 0 $ state, such as$ \pi_1^0\to \eta\pi^0 $ and$ \eta'\pi^0 $ , the couplings involve interferences between the processes illustrated in Fig. 1 (a) and (b). Because the mixing angle between η and$ \eta' $ is$ \alpha_P\simeq 42^\circ $ , the couplings for the channels between η and$ \eta' $ would be significantly different.●
$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ -decays into$ \pi\pi $ and$ K\bar{K} $ are forbidden by the Bose symmetry and G-parity conservation. They can only access$ \eta\eta' $ via the octet and singlet mixing. The coupling strengths exhibit non-trivial dependence on the mixing angle α. It can be observed that the decay pattern for these channels in a combined analysis should be sensitive to the value of α. -
A typical process for the production of a
$ J^{PC}=1^{-+} $ hybrid in the$ J/\psi $ -radiative decays is illustrated by Fig. 2. This figure demonstrates that the annihilations of the charm and anti-charm quark can create a pair of light S-wave$ q\bar{q} $ associated by a constituent gluon in a relative P-wave to the$ q\bar{q} $ . At the hadronic level, the Lagrangian for a general vector-vector-vector field interaction at the leading-order can be described by
Figure 2. (color online) Illustration of the
$ 1^{-+} $ isoscalar hybrid production in$ J/\psi\to \gamma \eta_1 $ .$ {\cal{L}}_{VVV}={\rm i}g_{VVV}(V_{1,\nu}\overleftrightarrow{\partial^{\mu}}V_2^{\nu}V_{3,\mu}+V_{1,\mu}V_2^{\nu}\overleftrightarrow{\partial^{\mu}}V_{3,\nu}+V_{2,\mu}V_3^{\nu}\overleftrightarrow{\partial^{\mu}}V_{1,\nu})\ , $

(10) where
$ V_1 $ ,$ V_2 $ , and$ V_3 $ denote the vector fields. For the radiative decay of$ J/\psi\to\gamma \eta_1 $ , because the photon is transversely polarized, the above Lagrangian will reduce to the following form:$ {\cal L}_{J/\psi\to \gamma \eta_1} = {\rm i}g_{J/\psi \eta_1\gamma}F_{\mu\nu}V_{J/\psi}^\mu V_{\eta_1}^\nu \ , $

(11) where
$ F_{\mu\nu}\equiv \partial_\mu A_\nu-\partial_\nu A_\mu $ , while the vector fields$ V_{J/\psi} $ , A, and$ V_{\eta_1} $ represent the initial$ J/\psi $ , final-state photon, and hybrid$ \eta_1 $ fields, respectively;$ g_{J/\psi \eta_1\gamma} $ is the coupling constant. Note that the leading transition of$ J/\psi\to\gamma \eta_1 $ is via a P wave. In the center of mass (c.m.) frame of$ J/\psi $ , the squared transition amplitudes for the two$ I=0 $ states can be expressed as:$ |{\rm i}{\cal M}(J/\psi\to\gamma \eta_{1{\rm L}})|^2\propto g_{J/\psi \eta_{1{\rm L}}\gamma}^2|{\boldsymbol q}_{\rm L}|^2(1+m_{J/\psi}^2/m_{\eta_{1{\rm L}}}^2) \ , $

(12) $ |{\rm i}{\cal M}(J/\psi\to\gamma \eta_{1{\rm H}})|^2 \propto g_{J/\psi \eta_{1{\rm H}}\gamma}^2|{\boldsymbol q}_{\rm H}|^2(1+m_{J/\psi}^2/m_{\eta_{1{\rm H}}}^2)\ , $

(13) where
$ {\boldsymbol q}_{\rm L} $ and$ {\boldsymbol q}_{\rm H} $ are the three-vector momenta of$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ in the$ J/\psi $ rest frame, respectively. The subscripts, "L" and "H" represent the low and high mass states, respectively. The two coupling constants,$ g_{J/\psi \eta_{1{\rm L}}\gamma} $ and$ g_{J/\psi \eta_{1{\rm H}}\gamma} $ , which account for the production mechanism for these two isoscalars, can be parametrized out:$ g_{J/\psi \eta_{1{\rm L}}\gamma} = g_0(\sqrt{2}\cos\alpha-R\sin\alpha) \ , $

(14) $ g_{J/\psi \eta_{1{\rm H}}\gamma} = g_0(\sqrt{2}\sin\alpha+R\cos\alpha) \ , $

(15) where
$ R\simeq f_\pi/f_K\simeq 0.93 $ indicates the SU(3) flavor symmetry breaking effects in the production of the$ s\bar{s} $ pair in comparison with the non-strange$ q\bar{q} $ pairs, and$ g_0 $ describes the coupling strength for the production of a light hybrid configuration$ q\bar{q}\tilde{g} $ of$ J^{PC}=1^{-+} $ in the$ J/\psi $ radiative decays. It can be expressed as$ g_0\equiv \langle (q\bar{q}\tilde{g})_{1^{-+}} |\hat{H}_{em}|J/\psi\rangle \ , $

(16) where
$ \hat{H}_{em} $ contains the dynamics for the transition in Fig. 2.The coupling relationship in Eq. (15) leads to the relative production rate for
$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ as follows:$ \begin{aligned}[b] r_{\rm L/H} \equiv & \frac{BR(J/\psi\to\gamma \eta_{1{\rm L}})}{BR(J/\psi\to\gamma \eta_{1{\rm H}})}\\=& \left(\frac{|{\boldsymbol q}_{\rm L}|}{|{\boldsymbol q}_{\rm H}|}\right)^3\frac{(\sqrt{2}\cos\alpha-R\sin\alpha)^2}{(\sqrt{2}\sin\alpha+R\cos\alpha)^2}\frac{m_{\eta_{1{\rm H}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm L}}}^2)}{m_{\eta_{1{\rm L}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm H}}}^2)} \ , \end{aligned} $

(17) which seems to be sensitive to the mixing angle α. Note that, in Refs. [1, 2] the
$ \eta_1(1855) $ signal is actually observed in its decays into$ \eta\eta' $ . Moreover, the PWA results suggest that only one$ I=0 $ hybrid state has been clearly observed in the$ 1^{-+} $ partial wave amplitude. As illustrated in Subsection II.B, the decays of$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ into$ \eta\eta' $ are strongly correlated with the mixing angle α and mechanisms for the flux tube breaking. This implies that the following branching ratio fractions can serve as constraints on the mixing angle:$ \begin{aligned}[b]& {\bf{Scheme-I}} :\\& R_{\eta_{1{\rm L}}/\eta_1(1855)}\equiv \frac{BR(J/\psi\to\gamma \eta_{1{\rm L}}\to\gamma\eta\eta')}{BR(J/\psi\to\gamma \eta_1(1855)\to\gamma\eta\eta')} < 10 {\text{%}} \ , \end{aligned}$

(18) and
$ \begin{aligned}[b]& {\bf{Scheme-II}} :\\& R_{\eta_{1{\rm H}}/\eta_1(1855)}\equiv \frac{BR(J/\psi\to\gamma \eta_{1{\rm H}}\to\gamma\eta\eta')}{BR(J/\psi\to\gamma \eta_1(1855)\to\gamma\eta\eta')} < 10 {\text{%}} \ , \end{aligned}$

(19) where we have assigned
$ \eta_1(1855) $ as either the higher mass state (Scheme-I) or the lower mass state (Scheme-II). The relative rate (10%) is the production upper limit for the partner of$ \eta_1(1855) $ from the experimental measurement [1, 2].With the earlier extracted production and decay couplings, the general form for the joint branching ratio fraction can be expressed as:
$ \begin{aligned}[b] &R_{\eta_{1{\rm L}}/\eta_{1{\rm H}}} \\=& \left(\frac{|{\boldsymbol q}_{\rm L}|}{|{\boldsymbol q}_{\rm H}|}\right)^3\frac{(\sqrt{2}\cos\alpha-R\sin\alpha)^2}{(\sqrt{2}\sin\alpha+R\cos\alpha)^2}\frac{m_{\eta_{1{\rm H}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm L}}}^2)}{m_{\eta_{1{\rm L}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm H}}}^2)} \\&\times\left(\frac{|{\boldsymbol k}_{\rm L}|}{|{\boldsymbol k}_{\rm H}|}\right)^3 \left(\frac{\Gamma_{\rm H}m_{\eta_{1{\rm H}}}}{\Gamma_{\rm L}m_{\eta_{1{\rm L}}}}\right)^2 \\ & \times \frac{[(1+\delta)\tan 2\alpha_P(\cos\alpha+R\sin\alpha)+2 \delta(R\cos\alpha-\sin\alpha)]^2}{[(1+\delta)\tan 2\alpha_P(\sin\alpha-R\cos\alpha)+ 2\delta(R\sin\alpha+\cos\alpha)]^2} \ , \end{aligned} $

(20) where
$ \Gamma_{\rm L} $ and$ \Gamma_{\rm H} $ represent the total widths of the lower and higher mass states, respectively;$ {\boldsymbol q}_{\rm L,H} $ and$ {\boldsymbol k}_{\rm L,H} $ denote the three-vector momenta of the photon and pseudoscalar meson in the rest frames of$ J/\psi $ and$ \eta_{\rm L,H} $ , respectively; and$ \delta\equiv g_2/g_1 $ indicates the relative strength between the two decay mechanisms for the flux tube breaking. As discussed earlier,$ |\delta|\simeq 1 $ is for the hybrid decays, while$ |\delta|<< 1 $ is for conventional$ q\bar{q} $ decays. In Eq. (21), if we approximate$ {\Gamma_{\rm H}}/{\Gamma_{\rm L}}\simeq 1 $ , the ratio$ R_{\eta_{1{\rm L}}/\eta_{1{\rm H}}} $ will strongly depend on α and δ. -
Before we go into the detailed studies of the two schemes, we briefly summarize the present experimental information on the strange vector mesons. As presented by the Particle Data Group (PDG) [36], two excited
$ K^* $ states are observed in the experiment, i.e.$ K^*(1410) $ and$ K^*(1680) $ . Although$ K^*(1410) $ can be well accommodated by the first radial excitations of the vector meson nonet, the property of$ K^*(1680) $ is far from being well explored. Note that the second radial excitations of the isoscalar pseudoscalar mesons can be occupied by$ \eta(1760) $ and$ \eta(1860) $ in the Regge trajectory [37], and the mass of$ K^*(1680) $ , as the second radial excitation in the conventional$ q\bar{q} $ vector nonet, tends to be negligible. We also note that the strange pseudoscalar partner in the second radial excitation nonet has not yet been established in experiments, although$ K(1630) $ could be a candidate [36]. In the following analysis, we first consider$ K^*(1680) $ as the strange partner of the$ 1^{-(+)} $ nonet and examine whether it fits the constraint. Otherwise, we investigate the mass correlation of$ K^* $ with the mixing angle and other multiplets as required by the Gell-Mann-Okubo relationship. -
With the
$ \eta_1(1855) $ assigned as the higher mass state, and$ \pi_1(1600) $ and$ K^*(1680) $ assigned as the$ I=1 $ and strange partner, respectively, we extract$ m_{\eta_{1{\rm L}}}=1712.5\pm $ $ 8.7 $ MeV from Eq. (7), and the mixing angle$ \alpha=30^\circ\pm $ $ 13^\circ $ . The uncertainties are given by the mass uncertainties from$ \pi_1(1600) $ and$ K^*(1680) $ via the Gell-Mann-Okubo relationship. We note that the PDG values [36] are adopted for the masses of these two states, i.e.$ m_{\pi_1}=1661\pm 13 $ MeV and$ m_{K^*}=1718\pm 18 $ MeV. From Eq. (6), we can extract the correlation between the mixing angle and the$ K^* $ mass, and the obtained results are presented in Fig. 3.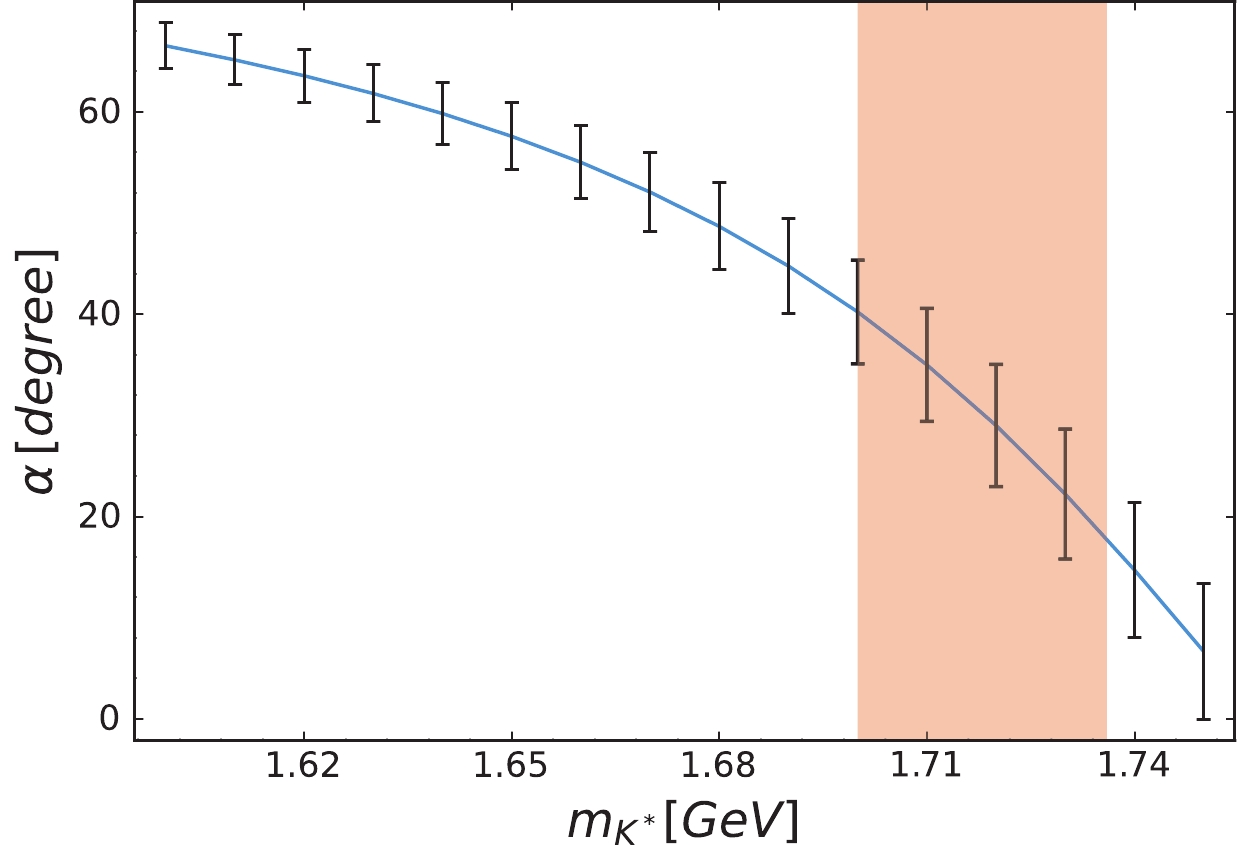
Figure 3. (color online) Correlation of the mixing angle α with the
$ K^* $ mass. The uncertainties are due to the mass uncertainties for those input states. The shadowed area indicates the mass range of$ K^* $ from PDG [36].Although the uncertainties of the mixing angle α tend to be rather large, it indicates significant mixings between the flavor octet and singlet, and apparently deviates from the ideal mixing. This appears to be a necessary consequence provided there is only one
$ I=0 $ hybrid state observed in the$ \eta\eta' $ channel in$ J/\psi\to\gamma\eta\eta' $ . Nevertheless, it favors the hybrid scenario to have important contributions from the transverse mode of the flux tube motions. To illustrate this, we first consider Eq. (18), where by taking the limit of ideal mixing, i.e.$ \alpha=0^\circ $ , the production ratio$ r_{\rm L/H}\simeq 2 $ can be obtained. Note that the ratio$ r_{\rm L/H} $ is insensitive to the phase space factor and SU(3) flavor symmetry breaking parameter R.In the case where
$ \eta_1(1855) $ is the higher mass state, the ratio$ R_{\eta_{1{\rm L}}/\eta_{1{\rm H}}} $ defined in Eq. (21) can be compared with the experimental observables with$ R_{\eta_{1{\rm L}}/\eta_1(1855)} $ < 10%. In the ideal mixing limit, we have$ \begin{aligned}[b]R_{\eta_{1{\rm L}}/\eta_1(1855)} \simeq & \left(\frac{|{\boldsymbol q}_{\rm L}|}{|{\boldsymbol q}_{\rm H}|}\right)^3\left(\frac{|{\boldsymbol k}_{\rm L}|}{|{\boldsymbol k}_{\rm H}|}\right)^3\frac{m_{\eta_{1{\rm H}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm L}}}^2)}{m_{\eta_{1{\rm L}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm H}}}^2)}\\&\times \left(\frac{\Gamma_{\rm H}m_{\rm H}}{\Gamma_{\rm L}m_{\rm L}}\right)^2 \frac{2}{R^2}\left[\frac{(1+\delta)\tan 2\alpha_P+2R\delta}{R(1+\delta)\tan 2\alpha_P-2\delta}\right]^2 \ . \end{aligned} $

(21) Note that the product
$\left(\dfrac{|{\boldsymbol q}_{\rm L}|}{|{\boldsymbol q}_{\rm H}|}\right)^3\left(\dfrac{|{\boldsymbol k}_{\rm L}|}{|{\boldsymbol k}_{\rm H}|}\right)^3\dfrac{m_{\eta_{1{\rm H}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm L}}}^2)}{m_{\eta_{1{\rm L}}}^2(m_{J/\psi}^2+m_{\eta_{1{\rm H}}}^2)} $ $ \left(\dfrac{\Gamma_{\rm H}m_{\rm H}}{\Gamma_{\rm L}m_{\rm L}}\right)^2$ actually enhances the ratio, while$ \tan 2\alpha_P\simeq 10 $ will further push the ratio up. It thus relies on the value of δ to decide the value of$ R_{\eta_{1{\rm L}}/\eta_{1{\rm H}}} $ . As discussed earlier, for conventional$ q\bar{q} $ meson decays, one would expect$ \delta\to 0 $ . It actually leads to$ R_{\eta_{1{\rm L}}/\eta_{1{\rm H}}}>1 $ , which contradicts the experimental observation. For the hybrid decays, the transverse mode of the flux tube motions plays an important role in the decays. It implies that$ |\delta|\simeq 1 $ , or is even the dominant transition mechanism with$ |\delta|>1 $ . Eventually, to obtain$ R_{\eta_{1{\rm L}}/\eta_1(1855)} $ < 10%, as suggested by the experimental data, it is observed that δ should take a negative value, and the absolute value is at$ {\cal O}(1) $ .In Fig. 4, with the mixing angle α within its uncertainty range, i.e.
$ \alpha=30^\circ\pm 13^\circ $ , we plot the ratios$ r_{\rm L/H} $ and$ R_{\eta_{1{\rm L}}/\eta_1(1855)} $ . For demonstration, we adopt$ \delta=-0.8, \ \ -1.0, \ -1.2 $ to calculate$ R_{\eta_{1{\rm L}}/\eta_1(1855)} $ . It shows that$ r_{\rm L/H} $ is not sufficiently suppressed while the decays via the transverse mode play a dominant role in suppressing the low-mass state. Although we cannot provide a precise value for δ based on the present experimental results, we deduce that the relative sign between$ g_1 $ and$ g_2 $ and their relative strength can consistently reflect the hybrid features.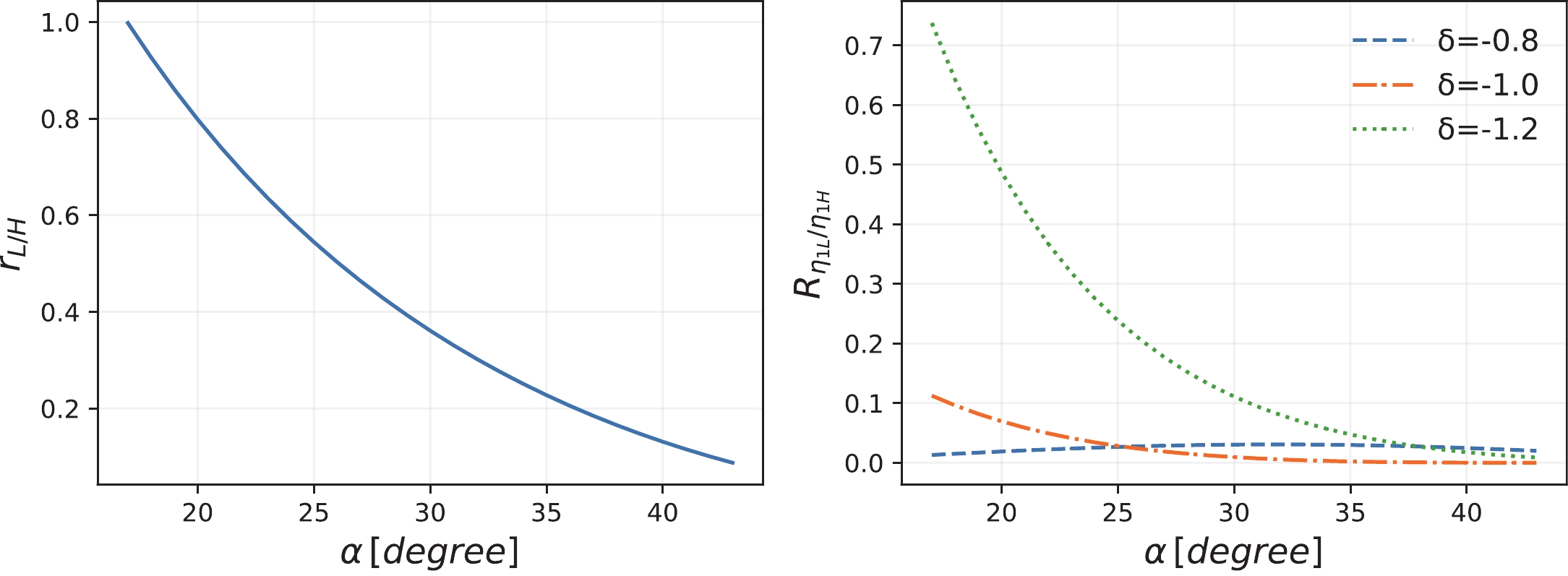
Figure 4. (color online) Dependence of the ratios
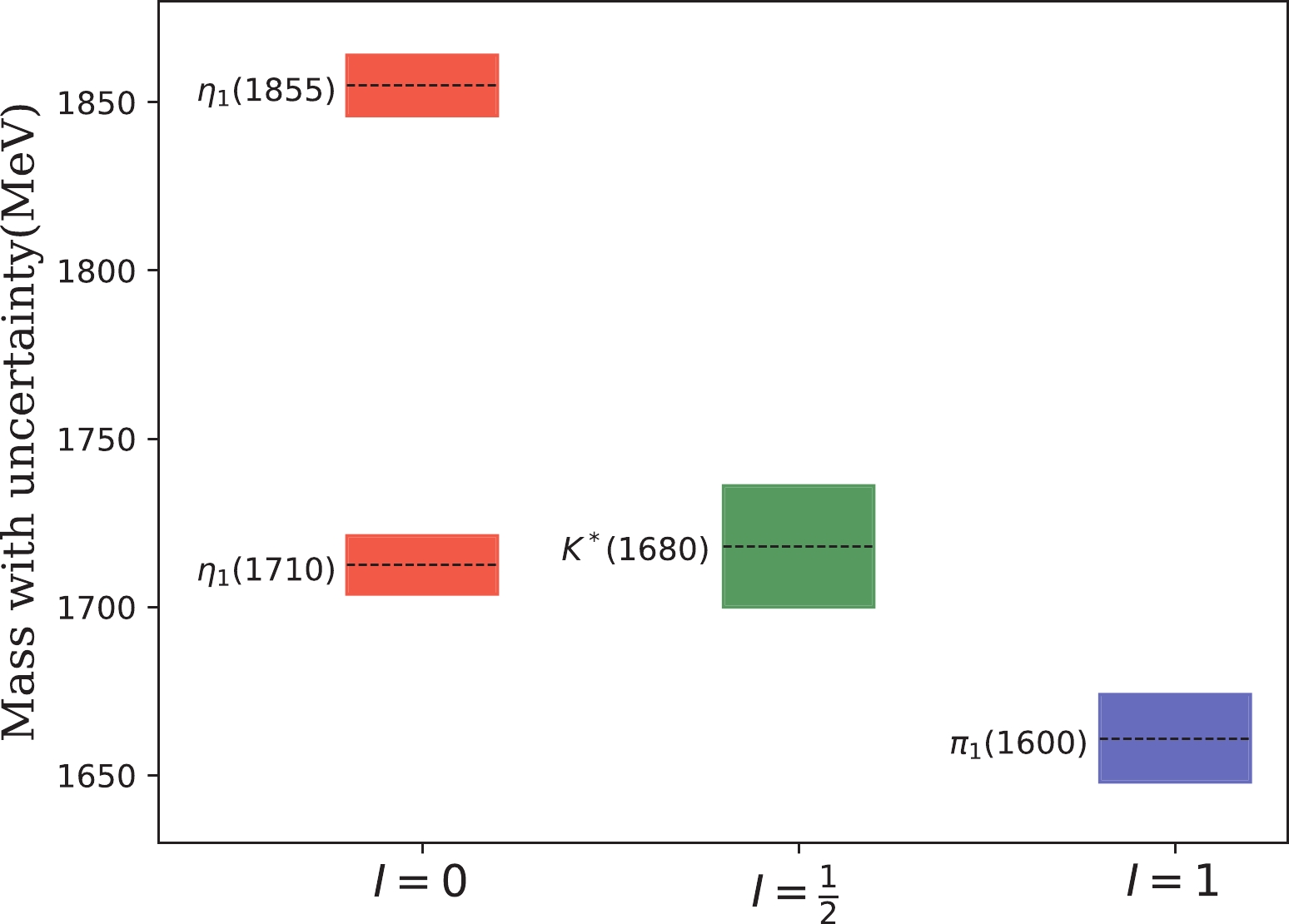
$ r_{\rm L/H} $ and$ R_{\eta_{1{\rm L}}/\eta_1(1855)} $ on the mixing angle α within the preferred range of$ \alpha\in (17^\circ, \ 43^\circ) $ . In Scheme-I$ \eta(1855) $ is the high-mass state. On the left panel the solid line is for$ r_{\rm L/H} $ , while on the right panel the dashed, dot-dashed, and dotted lines correspond to the ratio$ R_{\eta_{1{\rm L}}/\eta_1(1855)} $ with$ \delta=-0.8, \ -1.0, \ -1.2 $ , respectively.In Fig. 5, we illustrate the
$ 1^{-(+)} $ nonet in Scheme-I. The shadowed ranges depict the mass uncertainties while the central dashed lines denote the preferred mass. -
With the
$ \eta_1(1855) $ assigned as the lower mass state, and$ \pi_1(1600) $ maintained as the$ I=1 $ partner, the determination of the lower$ I=0 $ state will be differently correlated with the mass of the strange partner. This implies that$ K^*(1680) $ is no longer suitable for being the strange partner of the nonet. This can be easily observed using Eq. (7), which is symmetric to$ \eta_{1{\rm L}} $ and$ \eta_{1{\rm H}} $ . If the same$ K^* $ mass is taken, the solution for the other$ \eta_1 $ mass will be a lower one, as in Scheme-I, and$ \eta_1(1855) $ will be maintained at a higher mass state.Therefore, searching for the higher mass partner of
$ \eta_1(1855) $ requires a higher$ K^* $ mass as input. As discussed earlier, to date, we still lack experimental information about the vector strange spectrum. Fortunately, if we impose the BESIII observation as a constraint again, we should obtain the inverse form of Eq. (21) to satisfy Eq. (20). In such a case, we determine that the mixing angle remains located around$ \alpha\in (25^\circ, 45^\circ) $ corresponding to$ m_{K^*}\simeq 1.83\sim 1.90 $ GeV. Meanwhile, it shows that δ remains at$ {\cal O}(1) $ , but favors a positive sign. In fact, the sign and magnitude of δ turn out to be very sensitive to the experimental constraint, which can be analytically observed using Eq. (21).Similar to Fig. 3, we plot in Fig. 6, the correlation between the mixing angle α and the
$ K^* $ mass. The preferred$ K^* $ mass is$ m_{K^*}\simeq 1.83\sim 1.90 $ GeV corresponding to the range of$ \alpha=25^\circ\sim 45^\circ $ .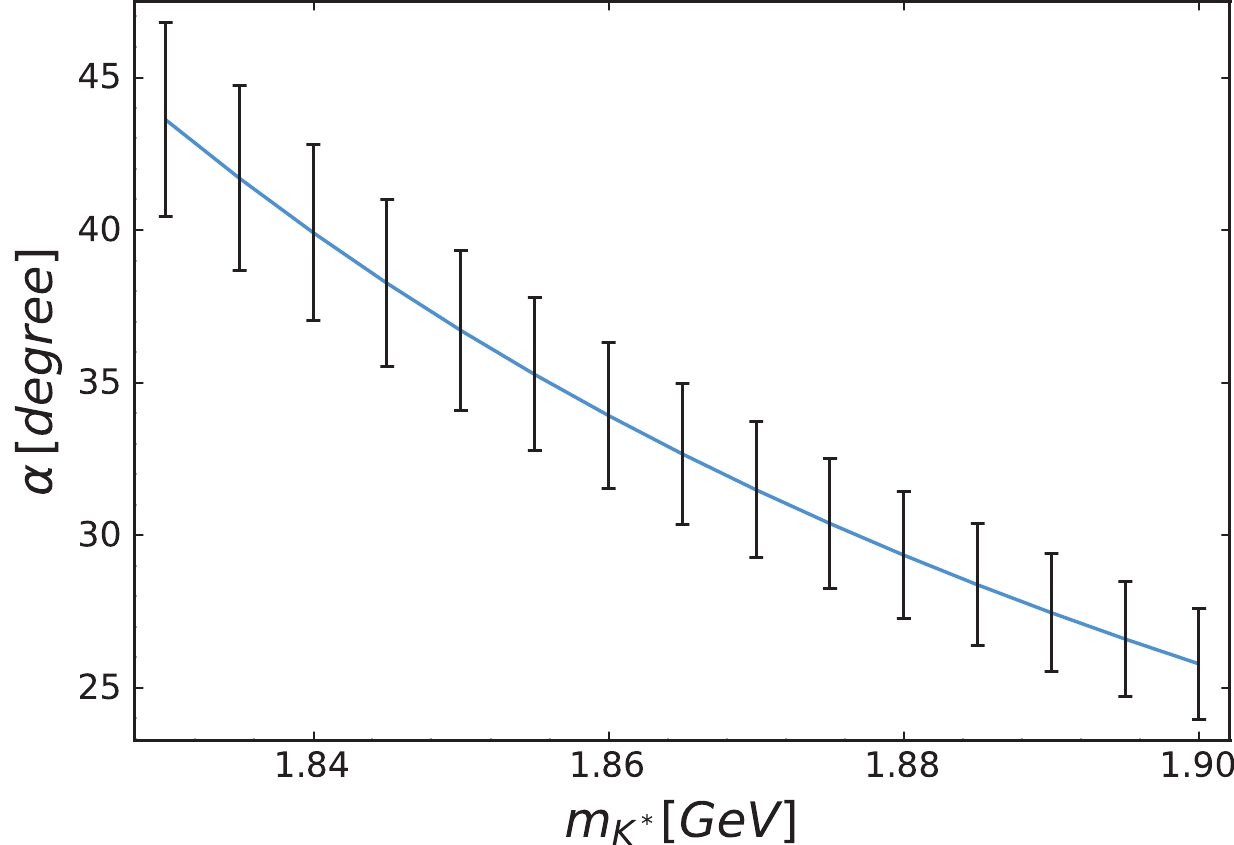
Figure 6. (color online) Correlation of the mixing angle α with the
$ K^* $ mass in Scheme-II. The uncertainties are due to the mass uncertainties for those input states.In Fig. 7, we present the results for
$ r_{\rm H/L} $ and$ R_{\eta_{1{\rm H}}/\eta_1(1855)} $ in terms of the mixing angle α within its uncertainty range, i.e.$ \alpha= 25^\circ\sim 45^\circ $ . It is interesting to see that in Scheme-II, the production of$ \eta(1855) $ in$ J/\psi\to \gamma \eta_{\rm 1L, 1H} $ as the low-mass state is actually comparable with the higher one. It is the decay transition of$ \eta_{\rm 1L}\to\eta\eta' $ that strongly enhances the signal of$ \eta_1(1855) $ in the$ \eta\eta' $ channel while the higher mass state is suppressed owing to its weak coupling to the$ \eta\eta' $ channel. Again, we observe the dominance of the transverse mode in the hybrid decays. For demonstrations, we adopt$ \delta=0.8, \ 1.0, \ 1.2 $ to calculate$ R_{\eta_{\rm 1H}/\eta_1(1855)} $ , which are presented on the right panel of Fig. 7.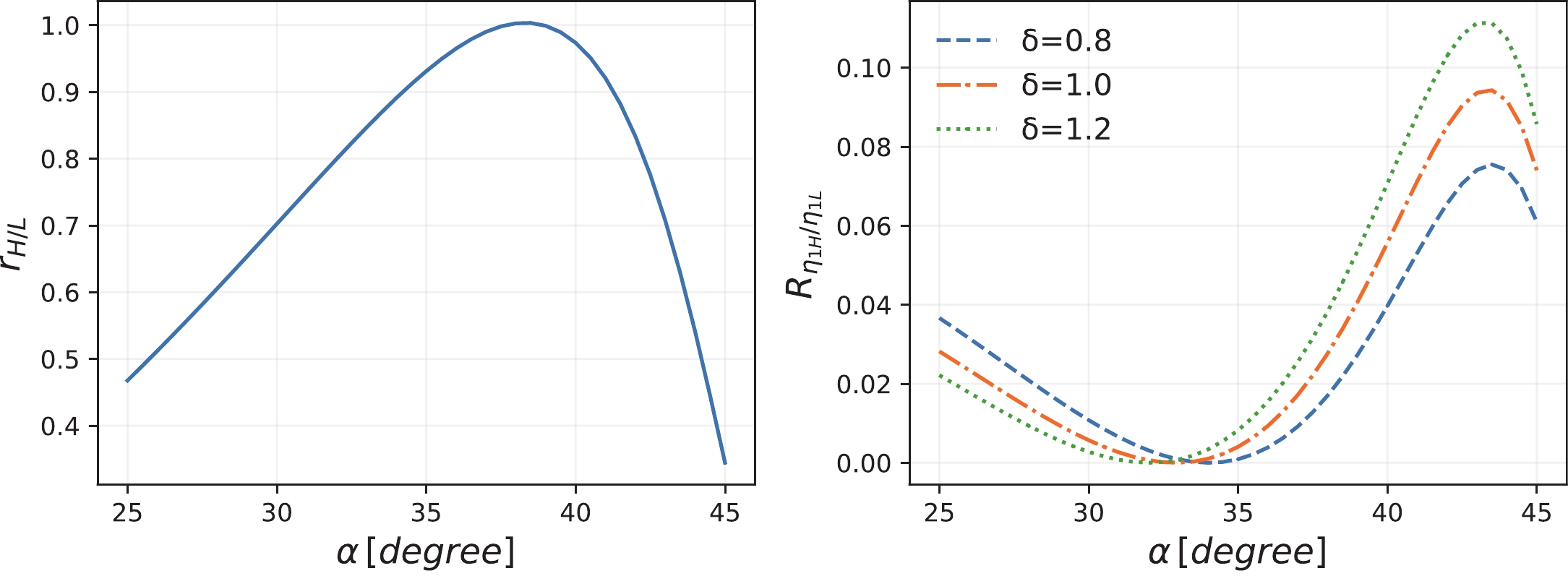
Figure 7. (color online) The dependence of the ratios
$ r_{\rm H/L} $ and$ R_{\eta_{1{\rm H}}/\eta_1(1855)} $ on the mixing angle α within the preferred range of$ \alpha\in (25^\circ, \ 45^\circ) $ . In Scheme-II,$ \eta_1(1855) $ is the low-mass state. On the left panel the solid line is for$r_{\rm H/L}$ , while on the right panel the dashed, dot-dashed, and dotted lines correspond to the ratio$ R_{\eta_{1{\rm H}}/\eta_1(1855)} $ with$ \delta=0.8, \ 1.0, \ 1.2 $ , respectively.In Fig. 8, we illustrate the
$ 1^{-(+)} $ nonet in Scheme-II. The shadowed ranges represent the mass uncertainties and the central dashed lines denote the preferred mass.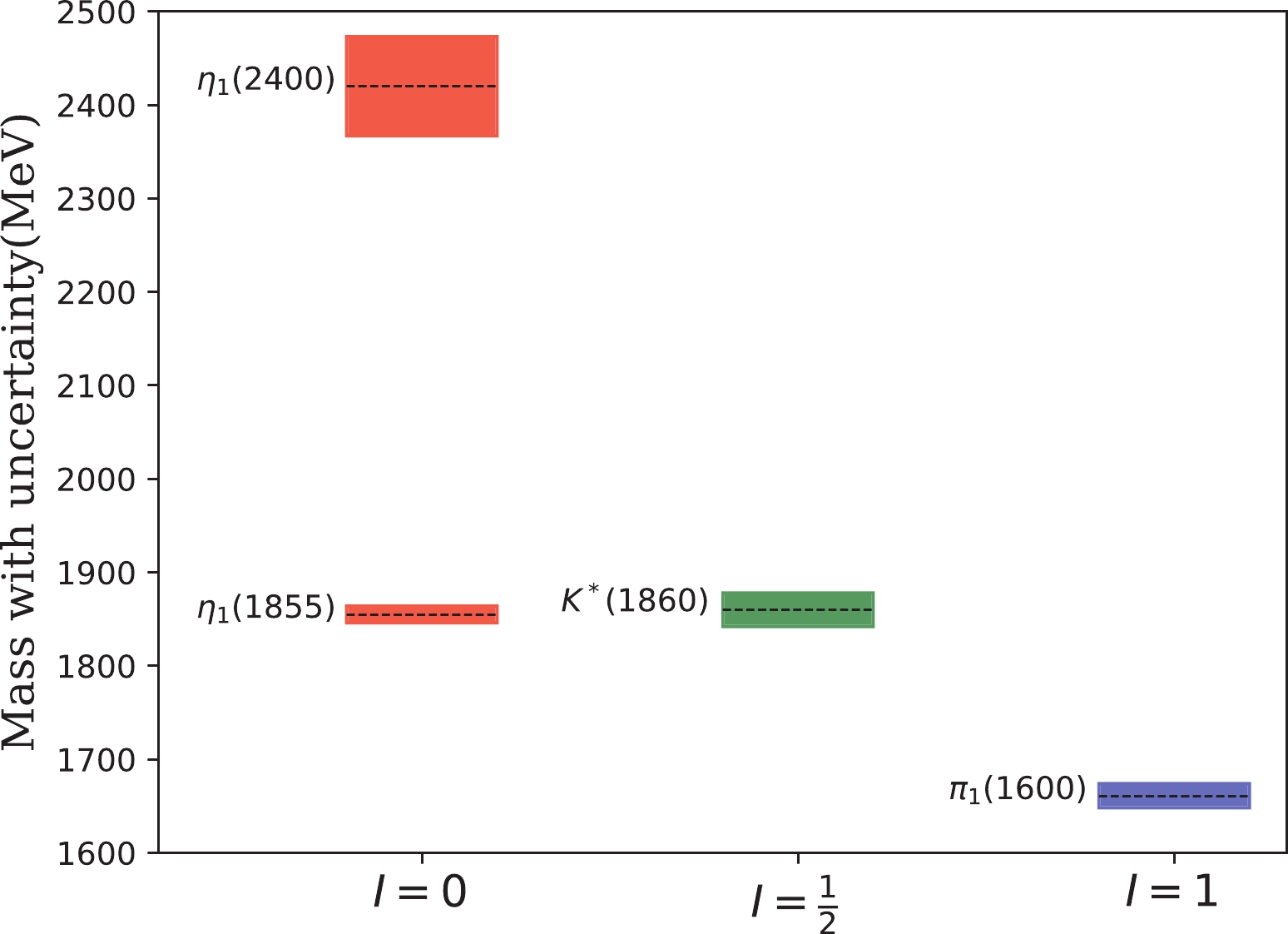
Figure 8. (color online) The
$ 1^{-(+)} $ hybrid nonet with mass uncertainties determined in Scheme-II. Namely,$ \eta_1(1855) $ is assigned as the lower mass state with$ I=0 $ .Comparing these two nonet schemes, it demonstrates that the transverse mode plays an important role for understanding the decay pattern observed in experiment. The relative sign between the transverse and longitudinal modes should decide the scheme that is the physical one. However, based on the present experimental information, it is impossible to conclude. We would look forward to further observations, to provide a constraint on the sign from the experiment. Meanwhile, we note that the LQCD calculations of these two decay modes may also be beneficial in determining their relative signs.
-
To further investigate the characters emerging from the nonet structure of the
$ 1^{-(+)} $ hybrid states, we analyze the hadronic decays of$ J/\psi\to V H $ and search for signals for the$ I=0 $ partner of$ \eta_1(1855) $ . Here, V denotes the vector mesons ρ, ω, and ϕ, while H represents the light hybrid multiplets. This process is illustrated in Fig. 9, and the leading-order Lagrangian is given in Eq. (10). The coupling for$ J/\psi\rightarrow [q\bar{q}]_{1^{–}}[q\bar{q}\tilde{g}]_{1^{-+}} $ can be parametrized as
Figure 9. (color online) Illustration of the production process for the
$ 1^{-(+)} $ hybrid states in$ J/\psi\to VH $ where V denotes the light vector mesons ρ, ω, ϕ and$ K^*(892) $ .$ g_P\equiv \langle [q\bar{q}]_{1^{–}}[q\bar{q}\tilde{g}]_{1^{-+}} |\hat{V}_P|J/\psi\rangle \ , $

(22) where
$ \hat{V}_P $ represents the potential for the hadronic decays of$ J/\psi\to VH $ . In addition, the detailed coupling constants for different decay channels are expressed as follows:$ \begin{aligned}[b] \quad g_{J/\psi\rho^+\pi_1^-} =& g_P ,\\ g_{J/\psi\omega\eta_{1{\rm L}}} =& g_P\cos\alpha \ ,\\ g_{J/\psi\omega\eta_{1{\rm H}}} =& g_P\sin\alpha \ ,\\ g_{J/\psi\phi\eta_{1{\rm L}}} = & -g_P R^2 \sin\alpha \ ,\\ g_{J/\psi\phi\eta_{1{\rm H}}} = & g_P R^2 \cos\alpha \ ,\\ g_{J/\psi K^{*+} K_{\rm H}^{*-}} =& g_P R \ , \end{aligned} $

(23) where R is the SU(3) flavor symmetry breaking factor defined earlier. In this Section, to distinguish the hybrid
$ K^* $ from$ K^*(892) $ , we denote it as$ K^*_{\rm H} $ . In addition to the partial wave factor ($ \propto |{\boldsymbol q}|^3 $ ), which should be included for each channel and a mass function that has the same form for each channel, the branching ratio fractions among all the$ VH $ decay channels will be driven by the following relative strengths:$ \begin{aligned}[b]& \rho^+\pi_1^- : \omega\eta_{1{\rm L}} : \omega\eta_{1{\rm H}} : \phi\eta_{1{\rm L}} : \phi\eta_{1{\rm H}} : K^{*+} K_{\rm H}^{*-} \\ =& 1 : \cos^2\alpha : \sin^2\alpha : R^4\sin^2\alpha : R^4\cos^2\alpha : R^2 \ . \end{aligned} $

(24) Note that for the total of
$ \rho\pi $ , a factor of 3 should be multiplied to the$ \rho^+\pi_1^- $ channel, while the total of$ K^*\bar{K}_{\rm H}+{\rm c.c.} $ , a factor of 4 should be multiplied to the$ K^{*+} K_{\rm H}^{*-} $ channel.If we consider the effects emerging from the partial wave factor and the SU(3) flavor symmetry breaking factor R, we observe that the
$ \rho\pi_1 $ channel has the largest branching ratio, while the production strengths for most of the other channels are actually comparable with$ \alpha\sim 30^\circ $ . In particular, this suggests that the production of$ \eta_{\rm 1L} $ and$ \eta_{\rm 1H} $ are accessible in the same channel such as$ J/\psi\to \omega\eta\eta' $ . This differs from the case of$ J/\psi\to\gamma\eta\eta' $ .It should also be interesting to study the
$ J/\psi\to $ $ K^* \bar{K}_{\rm H}^*+c.c. $ channel. Because$ K_{\rm H}^* $ has$ J^P=1^- $ , which is the same as the radial excitation states of the vector$ K^*(892) $ , it is difficult to identify the hybrid-like state. However, as discussed earlier, the isolated$ K^*(1680) $ , either as a radial excitation state of$ K^*(892) $ or a hybrid state, will provide crucial understandings on the$ K^* $ spectrum. In the hybrid scenario,$ K_{\rm H}^* $ will prefer decaying into$ K_1\pi\to K^*\pi\pi $ . This implies that$ J/\psi\to K\bar{K}\pi\pi\pi\pi $ will be ideal for the$ K_{\rm H}^* $ search.In Fig. 10, we plot the branching ratio fractions in Scheme-I for each channels with respect to
$ J/\psi\to\rho^+\pi_1^- $ , for which we set it as unity, while the other channels are normalized to the$ \rho^+\pi_1^- $ channel with$ R=0.93 $ adopted. The favored range of the mixing angle is approximately$ \alpha\in (17^\circ, 43^\circ) $ . However, a relatively broad range is plotted in Fig. 10 as an illustration. The dependence of the mixing angle produces certain patterns, which makes the combined study of the$ VH $ channel beneficial for the further verification of the$ 1^{-(+)} $ nonet.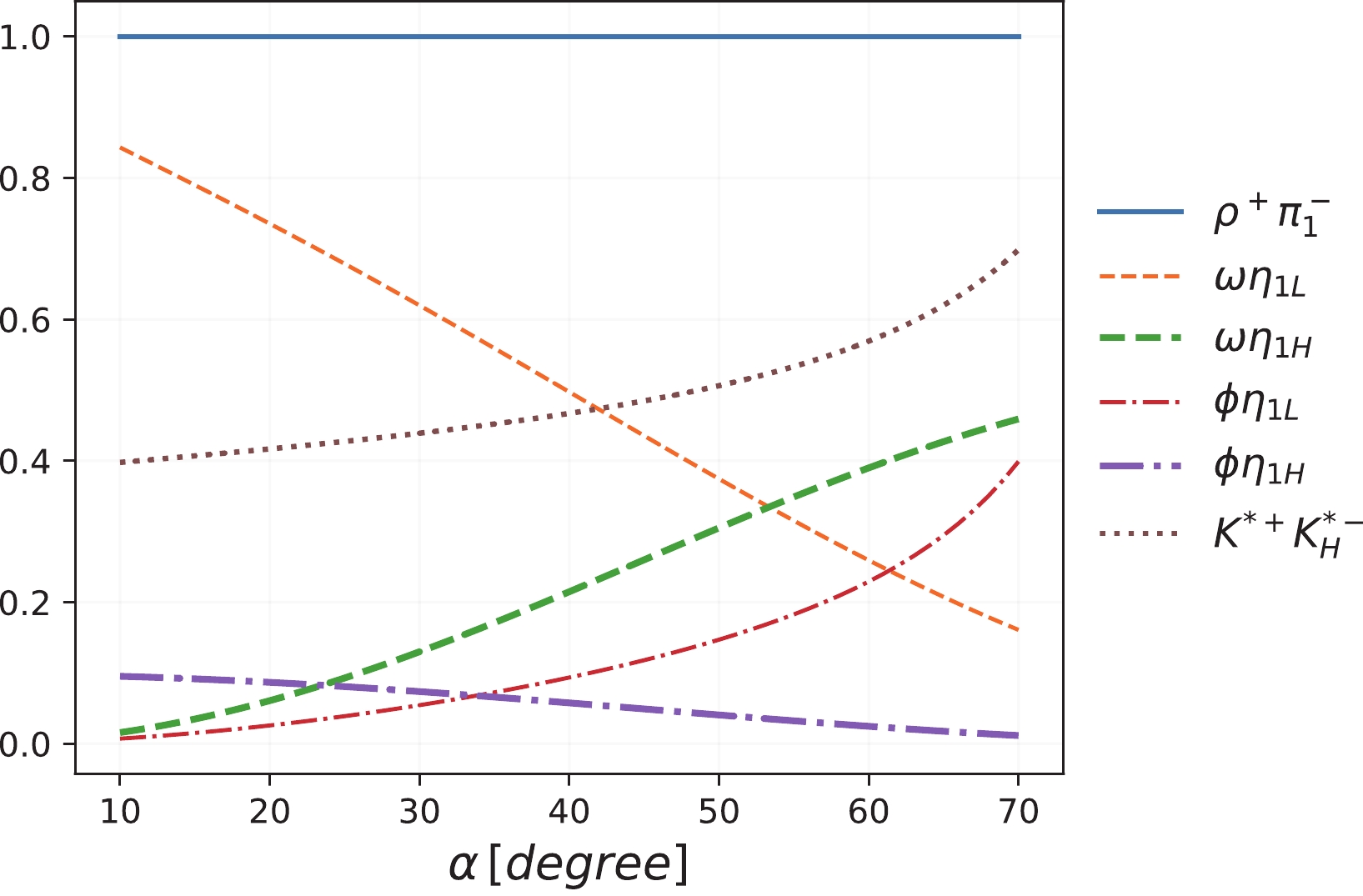
Figure 10. (color online) Predicted branching ratio fractions for
$ BR(J/\psi\to VH)/BR(J/\psi\to \rho^+\pi_1^-) $ in terms of α in Scheme-I.For the results of Scheme-II, the
$ \omega\eta_{\rm 1H} $ and$ \phi\eta_{\rm 1H} $ thresholds are higher than the$ J/\psi $ mass. A combined study can be conducted in other higher heavy quarkonium decays such as$ \Upsilon\to VH $ . -
Inspired by the observation of the isoscalar
$ 1^{-+} $ hybrid candidate$ \eta_1(1855) $ in$ J/\psi\to \gamma\eta_1(1855)\to\gamma\eta\eta' $ , we investigated its SU(3) flavor partners using a parametrization method based on the flux tube model picture. We demonstrated that, although the present experimental information remains limited, it could depict the$ 1^{-(+)} $ nonet of which the production and decays were consistent with the expectations of the flux tube model. We determined that the observation of a single$ \eta_1(1855) $ in the$ \eta\eta' $ channel is informative and can impose relatively strong constraints on the hybrid scenario. In particular, it suggests that the flavor octet and singlet mixing would be apparently deviated from the SU(3) ideal mixing, which indicates the importance of the quark annihilation effects. In the flux tube model, this implies that the transverse mode of the flux tube motions is important.We examined two schemes for the
$ 1^{-(+)} $ hybrid nonet by assigning the observed$ \eta_1(1855) $ to be either the high or low mass state with$ I=0 $ . In both cases, we determined that the requirement that one$ I=0 $ state should be highly suppressed in$ J/\psi\to\gamma\eta\eta' $ will also impose a strong constraint on the hybrid$ K^* $ mass. For the case in which$ \eta_1(1855) $ was the higher mass state,$ K^*(1680) $ appeared capable of filling the nonet chart reasonably well. For the case in which$ \eta_1(1855) $ was the lower mass state, a new state$ K^*(1860) $ was predicted. We deduced that one of the main differences between these two solutions lies on the relative sign between the transverse and longitudinal modes of the gluonic motions in the decay of the$ I=0 $ hybrid states. This implies that additional constraints from other processes are required. As a strongly correlated process, we suggest a combined study of$ J/\psi \to VH $ , to clarify the difference between these two schemes. Notice that the$ \rho\pi_1 $ production rate was expected to be significant and specific pattern actually emerged from the hybrid scenario. Hence, further evidences for$ \eta_1(1855) $ and its partner in$ J/\psi \to VH $ at BESIII would be crucial to ultimately establish the$ 1^{-(+)} $ nonet. -
The authors thank Xiao-Hai Liu and Alessandro Pilloni for their useful comments and discussions.
Towards the establishment of the light JP (C )=1–(+) hybrid nonet
- Received Date: 2022-02-07
- Available Online: 2022-05-15
Abstract: The observation of the light hybrid candidate






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: