-
The study on the internal structure of nucleon, as well as the spectrum and structures of nucleon resonances, allows access to the strong interaction and provides insight into the non-perturbative nature of quantum chromodynamics (QCD). Currently, most of our knowledge on the experimentally established nucleon resonances listed in the Review of Particle Physics (RPP) [1] primarily originates from the
$ \pi N $ scattering or$ \pi N $ ,$ \eta N $ ,$ K\Lambda $ , and$ K\Sigma $ photoproduction experiments. However, there might be nucleon resonances that have rather small couplings to the$ \pi N $ ,$ \eta N $ ,$ K\Lambda $ , and$ K\Sigma $ channels and are thus "missing" in these experiments. In fact, both the quark model [2, 3] and lattice QCD [4, 5] calculations predict significantly more nucleon resonances than those found in experiments. Inspired by this situation, in recent years, modern electromagnetic facilities around the world, such as the Thomas Jefferson National Accelerator Facility (JLab), Mainz Microtron (MAMI), 8 GeV Super Photon Ring (SPring-8), and Electron Stretcher Accelerator (ELSA), have measured large amounts of the data on both differential cross sections and polarization observables for$ \eta' N $ ,$ \omega N $ ,$ \phi N $ ,$ K^\ast \Lambda $ ,$ K^\ast \Sigma $ ,$ K\Lambda^\ast $ , and$ K\Sigma^\ast $ photoproduction processes. These measurements complement the results obtained from the$ \pi N $ scattering and the$ \pi N $ ,$ \eta N $ ,$ K\Lambda $ , and$ K\Sigma $ photoproduction experiments, by providing an alternative platform for finding new nucleon resonances and identifying the properties of some known nucleon resonances.The photoproduction of
$ K\Lambda^\ast $ , with$ \Lambda^\ast = \Lambda(1405) $ ,$ \Lambda(1520) $ ,$ \Lambda(1670) $ , or$ \Lambda(1690) $ , is suitable to study nucleon resonances with sizable hidden$ s\bar{s} $ components in a relatively less-explored higher energy region due to the much higher reaction thresholds of these channels. Besides, the s-channel isospin$ I = 3/2 \Delta $ and$ \Delta^\ast $ exchanges are forbidden from contributing to the$ K \Lambda^\ast $ photoproduction reactions, which simplifies the reaction mechanisms and facilitates the extraction of the information on the isospin$ I = 1/2 $ nucleon resonances. Compared with the photoproduction of$ K\Lambda $ , which has been widely studied in various approaches, e.g. chiral perturbation theory [6], isobar models [7-9], K-matrix approaches [10-12], and dynamical coupled-channels models [13, 14], the photoproduction of$ K \Lambda^\ast $ also has the advantage in that it may couple weakly to$ \pi N $ and$ \eta N $ channels owing to its significantly higher threshold, thereby leading to a substantially clearer background in isolating the complicated resonance contributions. In the literature, intensive experimental and theoretical analyses have been devoted to the investigations of the$ K \Lambda^\ast $ photoproduction reactions.In Refs. [15-17], the
$ K \Lambda(1405) $ photoproduction was studied based on the recent differential cross-section data from the CLAS Collaboration [18]. In Refs. [19-30], the$ K \Lambda(1520) $ photoproduction has been studied based on the recent measurements from the CLAS [18], LEPS [31] and SAPHIR [32] Collaborations, as well as the previous measurements at SLAC [33] and measurements from the LAPS2 group [34]. Unlike the photoproductions of$ K \Lambda(1405) $ and$ K \Lambda(1520) $ , which have been adequately investigated, theoretical investigations of the$ K\Lambda(1670) $ and$ K\Lambda(1690) $ photoproductions have been absent in the past owing to the lack of experimental data. Fortunately, the total cross-section data for$ K\Lambda(1670) $ and$ K\Lambda(1690) $ photoproduction reactions from the CLAS Collaboration became available recently [35]. The theoretical analyses of these data are called on to understand the underlying production mechanisms of these reactions.In this work, we concentrate on the investigation of the
$ \gamma p \to K^+\Lambda(1690) $ reaction. We construct a gauge-invariant model within the tree-level effective Lagrangian approach. The goal is to provide a theoretical description of the most recent total cross-section data from the CLAS Collaboration [35]. Accordingly, we attempt to elucidate the reaction mechanisms of this reaction and, in particular, extract the nucleon resonance contributions required in this reaction. We construct the reaction amplitudes for$ \gamma p \to K^+\Lambda(1690) $ by including the t-channel K and$ K^\ast $ exchanges, s-channel nucleon and nucleon resonance exchanges, and the interaction current, with the last one built in such a way that the full photoproduction amplitude satisfies the generalized Ward-Takahashi identity (WTI) and is thus fully gauge invariant. The results indicate that the available total cross-section data for$ \gamma p \to K^+\Lambda(1690) $ can be well reproduced by considering the s-channel$ N(2570)5/2^- $ exchange. The contributions from individual Feynman diagrams are analyzed. Furthermore, the differential cross sections are predicted and discussed, which can provide theoretical guidance for future experiments.The remainder of this paper is organized as follows. In Sec. II, the framework of our theoretical model is briefly introduced. The effective Lagrangians, resonance propagators, and phenomenological form factors adopted in the present calculations are comprehensively presented in this section. The numerical results are shown and discussed in Sec. III. Finally, the summary and conclusions of this paper are presented in Sec. IV.
-
In this study, we investigate the
$ \gamma p \to K^+\Lambda(1690) $ reaction in an effective Lagrangian approach at the tree-level approximation. For the convenience of further discussion, we define the Mandelstam variables$ t = (p-p^\prime)^2 = $ $ (k-q)^2 $ ,$ s = (p+k)^2 = (q+p^\prime)^2 = W^2 $ , and$ u = (p-q)^2 = $ $ (p^\prime-k)^2 $ as k, q, p, and$ p^\prime $ denoting the four-momenta of the incoming photon, outgoing K, initial-state proton, and final-state$ \Lambda(1690) $ , respectively.As depicted in Fig. 1, the following diagrams are included in constructing the reaction amplitudes: the s-channel nucleon and nucleon resonance exchanges, t-channel K and
$ K^\ast $ exchanges, and interaction current. Note that the u-channel Λ exchange is not considered, as no information on the radial decay$ \Lambda(1690) \to \Lambda \gamma $ is available in RPP [1]. The full amputated reaction amplitude for the$ \gamma p \to K^+\Lambda(1690) $ reaction can be expressed as
Figure 1. Generic structure of the amplitude for
$ \gamma p \to $ $ K^+\Lambda(1690) $ . Time proceeds from left to right. The outgoing$ \Lambda^\ast $ denotes$ \Lambda(1690) $ .$ \begin{equation} M^{\nu\mu} \equiv M^{\nu\mu}_s + M^{\nu\mu}_t + M^{\nu\mu}_{\rm{int}}, \end{equation} $

(1) where μ and ν denote the Lorentz indices of the incoming photon and outgoing
$ \Lambda(1690) $ , respectively.$ M^{\nu\mu}_s $ represents the s-channel amplitude of the nucleon and nucleon resonance exchanges, and$ M^{\nu\mu}_t $ is the t-channel amplitude comprising the K and$ K^\ast $ exchanges. They can be calculated straightforwardly with the effective Lagrangians, resonance propagators, and form factors given in the following part of this section.$ M^{\nu\mu}_{\rm{int}} $ in Eq. (1) represents the generalized interaction current arising from the photon attaching to the internal structure of the$ \Lambda(1690)NK $ vertex. It is known that in the effective Lagrangian approach, introducing the phenomenological form factors will result in violating the gauge invariance of the reaction amplitudes. In this study, we follow Refs. [36-45] to introduce an auxiliary current$ C^\mu $ and compensate the violation of the gauge invariance caused by the form factors; we model the generalized interaction current$ M^{\nu\mu}_{\rm{int}} $ as$ \begin{equation} M^{\nu\mu}_{\rm{int}} = \Gamma_{\Lambda^\ast NK}^\nu(q) C^\mu + M^{\nu\mu}_{\rm{KR}} f_t, \end{equation} $

(2) where
$ \Gamma_{\Lambda^\ast NK}^\nu(q) $ is the vertex function of the$ \Lambda(1690)NK $ interaction obtained from the Lagrangian of Eq. (13),$ \begin{equation} \Gamma_{\Lambda^\ast NK}^\nu(q) = - \frac{g_{\Lambda^\ast NK}}{M_K} \gamma_5 q^\nu, \end{equation} $

(3) and
$ M^{\nu\mu}_{\rm{KR}} $ is the traditional Kroll-Ruderman term obtained from the Lagrangian of Eq. (12),$ \begin{equation} M^{\nu\mu}_{\rm{KR}} = \frac{g_{\Lambda^\ast NK}}{M_K} g^{\nu\mu} \gamma_5 Q_K \tau, \end{equation} $

(4) with
$ Q_K $ being the electric charge of the outgoing K meson and τ being the isospin factor of the Kroll-Ruderman term.$ f_t $ is the phenomenological form factor attaching to the amplitude of the t-channel K exchange, which is given by Eq. (29). The auxiliary current$ C^\mu $ for the$ \gamma p \to K^+\Lambda(1690) $ reaction is chosen to be [41-43]$ \begin{equation} C^\mu = - Q_K \tau \frac{f_t-\hat{F}}{t-q^2} (2q-k)^\mu - \tau Q_N \frac{f_s-\hat{F}}{s-p^2} (2p+k)^\mu, \end{equation} $

(5) with
$ \begin{equation} \hat{F} = 1 - \hat{h} \left(1 - f_s\right) \left(1 - f_t\right). \end{equation} $

(6) Here,
$ Q_N $ represents the electric charge of N and$ f_s $ is the phenomenological form factor for the s-channel N exchange, as given in Eq. (30);$ \hat{h} $ is an arbitrary function tending to unity in the high-energy limit and set to be$ 1 $ in the present work for simplicity.The prescriptions of the generalized interaction current in Eq. (2) and the auxiliary current
$ C^\mu $ in Eq. (5) ensure that the full photoproduction amplitude of Eq. (1) satisfies the generalized WTI and is thus fully gauge invariant [41-43], independent of what particular forms are chosen for the phenomenological form factors$ f_s $ and$ f_t $ . -
In this subsection, the Lagrangians required to calculate the reaction amplitudes of the
$ \gamma p \to K^+\Lambda(1690) $ reaction are given. For convenience, we define the following operators:$ \begin{equation} \Gamma^{(+)} = \gamma_5, \qquad \Gamma^{(-)} = 1, \end{equation} $

(7) and the field-strength tensor for the photon field
$ A^\mu $ :$ \begin{equation} F^{\mu\nu} = \partial^\mu A^\nu - \partial^\nu A^\mu. \end{equation} $

(8) To avoid ambiguities, the notation
$ \Lambda^\ast $ will stand for only the$ \Lambda(1690) $ resonance throughout this paper.We use the following Lagrangians to calculate the non-resonant amplitudes
$ \begin{eqnarray} {\cal{L}}_{\gamma NN} = -\,e \bar{N} \left[ \left( \hat{e} \gamma^\mu - \frac{ \hat{\kappa}_N} {2M_N}\sigma^{\mu \nu}\partial_\nu \right) A_\mu\right] N, \end{eqnarray} $

(9) $ \begin{eqnarray} {\cal{L}}_{\gamma KK} = {\rm i}e \left[K^+\left(\partial_\mu K^-\right)-K^-\left(\partial_\mu K^+\right)\right] A^\mu, \end{eqnarray} $

(10) $ \begin{eqnarray} {\cal{L}}_{\gamma K{K^\ast}} = e\frac{g_{\gamma K{K^\ast}}}{M_K}\varepsilon^{\alpha \mu \lambda \nu}\left(\partial_\alpha A_\mu\right)\left(\partial_\lambda K\right) K^\ast_\nu, \end{eqnarray} $

(11) $ \begin{eqnarray} {\cal{L}}_{\gamma \Lambda^\ast NK} = -{\rm i}Q_K\frac{g_{\Lambda^\ast NK}}{M_K} \bar{\Lambda}^{\ast \mu} A_\mu K\gamma_5 N + {\rm{H}}{\rm{.c}}{\rm{.}}, \end{eqnarray} $

(12) $ \begin{eqnarray} {\cal{L}}_{\Lambda^\ast NK} = \frac{g_{\Lambda^\ast NK}}{M_K} {\bar{\Lambda}}^{\ast \mu} \left(\partial_\mu K\right)\gamma_5 N + {\rm{H}}{\rm{.c}}{\rm{.}}, \end{eqnarray} $

(13) $ \begin{eqnarray} {\cal{L}}_{\Lambda^\ast N K^\ast} = -\frac{{\rm i}\, g_{\Lambda^\ast N K^\ast}}{M_{K^\ast}}\bar{\Lambda}^{\ast \mu}\gamma^\nu \left(\partial_\mu K^{\ast}_\nu - \partial_\nu K^{\ast}_\mu \right)N + \, {\rm{H}}{\rm{.c}}{\rm{.}}, \\[-10pt]\end{eqnarray} $

(14) where
$ M_N $ ,$ M_K $ , and$ M_{K^\ast} $ denote the masses of N, K, and$ K^\ast $ , respectively. e is the elementary charge unit and$ \hat{e} $ stands for the charge operator acting on the nucleon field.$ \hat{\kappa}_N \equiv \kappa_p\hat{e} + \kappa_n(1-\hat{e}) $ with$ \kappa_p = 1.793 $ being the anomalous magnetic moment of proton and$ \kappa_n = -1.913 $ the anomalous magnetic moment of neutron. The coupling constants$ g_{\gamma K K^{\ast}} = 0.413 $ and$ g_{\Lambda^\ast NK} = 4.20 $ are calculated from the decay width of$ \Gamma(K^{*\pm}\to K^{\pm}\gamma) \approx 0.0503 $ MeV and$ \Gamma(\Lambda(1690)\to N\bar{K}) \approx 17.5 $ MeV, respectively, as given by RPP [1]. The coupling$ g_{\Lambda^\ast N K^\ast} $ is considered a free parameter to be determined by a fit to the data.For the s-channel resonance exchanges, the Lagrangians for the electromagnetic interactions are expressed as [30, 36-39]
$ \begin{eqnarray} {\cal{L}}_{RN\gamma}^{1/2\pm} = e\frac{g_{RN\gamma}^{(1)}}{2M_N}\bar{R} \Gamma^{(\mp)}\sigma_{\mu\nu} \left(\partial^\nu A^\mu \right) N + {\rm{H}}{\rm{.c}}{\rm{.}}, \end{eqnarray} $

(15) $ \begin{aligned}[b] {\cal{L}}_{RN\gamma}^{3/2\pm} = & -\, {\rm i}e\frac{g_{RN\gamma}^{(1)}}{2M_N}\bar{R}_\mu \gamma_\nu \Gamma^{(\pm)}F^{\mu\nu}N \\ &+\, e\frac{g_{RN\gamma}^{(2)}}{\left(2M_N\right)^2}\bar{R}_\mu \Gamma^{(\pm)}F^{\mu \nu}\partial_\nu N + {\rm{H}}{\rm{.c}}{\rm{.}}, \end{aligned} $

(16) $ \begin{aligned}[b] {\cal{L}}_{RN\gamma}^{5/2\pm} = & e\frac{g_{RN\gamma}^{(1)}}{\left(2M_N\right)^2}\bar{R}_{\mu \alpha}\gamma_\nu \Gamma^{(\mp)}\left(\partial^{\alpha} F^{\mu \nu}\right)N \\ & \pm\, {\rm i}e\frac{g_{RN\gamma}^{(2)}}{\left(2M_N\right)^3}\bar{R}_{\mu \alpha} \Gamma^{(\mp)}\left(\partial^\alpha F^{\mu \nu}\right)\partial_\nu N + \, {\rm{H}}{\rm{.c}}{\rm{.}}, \end{aligned} $

(17) $ \begin{aligned}[b] {\cal{L}}_{RN\gamma}^{7/2\pm} = & {\rm i}e\frac{g_{RN\gamma}^{(1)}}{\left(2M_N\right)^3}\bar{R}_{\mu \alpha \beta}\gamma_\nu \Gamma^{(\pm)}\left(\partial^{\alpha}\partial^{\beta} F^{\mu \nu}\right)N \\ &-\, e\frac{g_{RN\gamma}^{(2)}}{\left(2M_N\right)^4}\bar{R}_{\mu \alpha \beta} \Gamma^{(\pm)} \left(\partial^\alpha \partial^\beta F^{\mu \nu}\right) \partial_\nu N + \, {\rm{H}}{\rm{.c}}{\rm{.}}, \end{aligned} $

(18) and the Lagrangians for resonances coupling to
$ \Lambda(1690)K $ are [30]$ \begin{eqnarray} {\cal{L}}_{R\Lambda^\ast K}^{1/2\pm} = & \frac{g^{(1)}_{R\Lambda^\ast K}}{M_K} \bar{\Lambda}^{\ast\mu}\Gamma^{(\pm)} \left(\partial_\mu K\right) R + {\rm{H}}{\rm{.c}}{\rm{.}}, \end{eqnarray} $

(19) $ \begin{aligned}[b] {\cal{L}}_{R\Lambda^\ast K}^{3/2\pm} = & \frac{g^{(1)}_{R\Lambda^\ast K}}{M_K} \bar{\Lambda}^{\ast\mu}\gamma_\nu \Gamma^{(\mp)} \left(\partial^\nu K\right) R_\mu \\ & + \, {\rm i} \frac{g^{(2)}_{R\Lambda^\ast K}}{M_K^2} \bar{\Lambda}^\ast_\alpha \Gamma^{(\mp)} \left(\partial^\mu \partial^\alpha K\right) R_\mu + {\rm{H}}{\rm{.c}}{\rm{.}}, \end{aligned} $

(20) $ \begin{aligned}[b] {\cal{L}}_{R\Lambda^\ast K}^{5/2\pm} = & {\rm i}\frac{g^{(1)}_{R\Lambda^\ast K}}{M_K^2} \bar{\Lambda}^{\ast\alpha}\gamma_\mu \Gamma^{(\pm)} \left(\partial^\mu \partial^\beta K\right) R_{\alpha\beta} \\ &- \,\frac{g^{(2)}_{R\Lambda^\ast K}}{M_K^3} \bar{\Lambda}^\ast_\mu \Gamma^{(\pm)} \left(\partial^\mu \partial^\alpha \partial^\beta K\right) R_{\alpha\beta} + \, {\rm{H}}{\rm{.c}}{\rm{.}}, \end{aligned} $

(21) $ \begin{aligned}[b] {\cal{L}}_{R\Lambda^\ast K}^{7/2\pm} = & -\frac{g^{(1)}_{R\Lambda^\ast K}}{M_K^3} \bar{\Lambda}^{\ast\alpha}\gamma_\mu \Gamma^{(\mp)} \left(\partial^\mu \partial^\beta \partial^\lambda K\right) R_{\alpha\beta\lambda} \\ & - \, {\rm i} \frac{g^{(2)}_{R\Lambda^\ast K}}{M_K^4} \bar{\Lambda}^{\ast}_\mu \Gamma^{(\mp)} \left(\partial^\mu \partial^\alpha \partial^\beta \partial^\lambda K\right) R_{\alpha\beta\lambda} + \, {\rm{H}}{\rm{.c}}{\rm{.}}, \end{aligned} $

(22) where R denotes the
$ N^\ast $ resonance, and the superscripts of$ {\cal{L}}_{RN\gamma} $ and$ {\cal{L}}_{R\Lambda^\ast K} $ represent the spin and parity of the resonance R, respectively. In the this study, the$ g^{(2)}_{R\Lambda^\ast K} $ terms in$ {\cal{L}}_{R\Lambda^\ast K}^{3/2\pm} $ ,$ {\cal{L}}_{R\Lambda^\ast K}^{5/2\pm} $ , and$ {\cal{L}}_{R\Lambda^\ast K}^{7/2\pm} $ are ignored for simplicity. The products of the coupling constants$ g_{RN\gamma}^{(i)} g^{(1)}_{R\Lambda^\ast K} $ ($ i = 1,2 $ ) are considered fit parameters. -
The propagators of the
$ N^\ast $ resonance field (R) with mass$ M_R $ , width$ \Gamma_R $ , four-momentum p, and spin$ 1/2 $ ,$ 3/2 $ ,$ 5/2 $ , and$ 7/2 $ are expressed as [36, 46-48]$ \begin{eqnarray} S_{1/2}(p) = \frac{\rm i}{{\not{p}} - M_R + {\rm i} \Gamma_R/2}, \end{eqnarray} $

(23) $ \begin{eqnarray} S_{3/2}(p) = \frac{\rm i}{{\not{p}} - M_R + {\rm i} \Gamma_R/2} \left( \tilde{g}_{\mu \nu} + \frac{1}{3} \tilde{\gamma}_\mu \tilde{\gamma}_\nu \right), \end{eqnarray} $

(24) $ \begin{aligned}[b] S_{5/2}(p) = & \frac{\rm i}{{\not{p}} - M_R + {\rm i} \Gamma_R/2} \,\bigg[ \, \frac{1}{2} \big(\tilde{g}_{\mu \alpha} \tilde{g}_{\nu \beta} + \tilde{g}_{\mu \beta} \tilde{g}_{\nu \alpha} \big) \\ & -\, \frac{1}{5}\tilde{g}_{\mu \nu}\tilde{g}_{\alpha \beta} + \frac{1}{10} \big(\tilde{g}_{\mu \alpha}\tilde{\gamma}_{\nu} \tilde{\gamma}_{\beta} + \tilde{g}_{\mu \beta}\tilde{\gamma}_{\nu} \tilde{\gamma}_{\alpha} \\ & +\, \tilde{g}_{\nu \alpha}\tilde{\gamma}_{\mu} \tilde{\gamma}_{\beta} +\tilde{g}_{\nu \beta}\tilde{\gamma}_{\mu} \tilde{\gamma}_{\alpha} \big) \bigg], \end{aligned} $

(25) $ \begin{aligned}[b] S_{7/2}(p) = & \frac{\rm i}{{\not{p}} - M_R + {\rm i} \Gamma_R/2} \, \frac{1}{36}\sum_{P_{\mu} P_{\nu}} \bigg( \tilde{g}_{\mu_1 \nu_1}\tilde{g}_{\mu_2 \nu_2}\tilde{g}_{\mu_3 \nu_3} \\ & -\, \frac{3}{7}\tilde{g}_{\mu_1 \mu_2}\tilde{g}_{\nu_1 \nu_2}\tilde{g}_{\mu_3 \nu_3} + \frac{3}{7}\tilde{\gamma}_{\mu_1} \tilde{\gamma}_{\nu_1} \tilde{g}_{\mu_2 \nu_2}\tilde{g}_{\mu_3 \nu_3} \\ & -\, \frac{3}{35}\tilde{\gamma}_{\mu_1} \tilde{\gamma}_{\nu_1} \tilde{g}_{\mu_2 \mu_3}\tilde{g}_{\nu_2 \nu_3} \bigg), \end{aligned} $

(26) where
$ \begin{eqnarray} \tilde{g}_{\mu \nu} = -\, g_{\mu \nu} + \frac{p_{\mu} p_{\nu}}{M_R^2}, \end{eqnarray} $

(27) $ \begin{eqnarray} \tilde{\gamma}_{\mu} = \gamma^{\nu} \tilde{g}_{\nu \mu} = -\gamma_{\mu} + \frac{p_{\mu}{\not{p}}}{M_R^2}, \end{eqnarray} $

(28) and the summation over
$ P_\mu \left(P_\nu\right) $ in Eq. (26) goes over the$ 3! = 6 $ possible permutations of the indices$ \mu_1\mu_2\mu_3 \left(\nu_1\nu_2\nu_3\right) $ .In this study, the Rarita-Schwinger prescriptions for the propagators of high spin resonances are used in Eqs. (24)–(26). It is known that the Rarita-Schwinger prescriptions suffer from low-spin background problems. Efforts to determine the pure high-spin propagator formalism commenced in Ref. [49] and were later implemented for applications in nuclear and particle physics in Ref. [50]. In the future, when more data for
$ \gamma p \to K^+ \Lambda(1690) $ become available, a serious treatment of the resonance propagators, as discussed in Refs. [49, 50], will be required. -
In the effective Lagrangian approach, phenomenological form factors are introduced in hadronic vertices to consider the internal structures of hadrons and regularize the momentum dependence of the reaction amplitudes. In this study, we use the following form factors for the t-channel meson exchanges [30, 36-39]
$ \begin{eqnarray} f_M(q^2_M) = \left (\frac{\Lambda_M^2-M_M^2}{\Lambda_M^2-q^2_M} \right)^2, \end{eqnarray} $

(29) and for the s-channel baryon exchanges, we use [30, 36-39]
$ \begin{eqnarray} f_B(p^2_s) = \left (\frac{\Lambda_B^4}{\Lambda_B^4+\left(p_s^2-M_B^2\right)^2} \right )^2, \end{eqnarray} $

(30) where
$ q_M $ represents the four-momentum of the intermediate meson in the t channel,$ p_s $ stands for the four-momentum of the intermediate baryon in the s channel, and$ \Lambda_{M(B)} $ is the cutoff parameter. In this study, we adopt a common value for all the non-resonant diagrams, i.e.$ \Lambda_{\rm{bg}} \equiv \Lambda_K = \Lambda_{K^\ast} = \Lambda_N $ , to reduce the number of adjustable parameters. The parameter$ \Lambda_{\rm{bg}} $ and the cutoff parameter$ \Lambda_R $ for nucleon resonances are determined by fitting the experimental data.In addition to the dipole form factors adopted in this work, the monopole form factors and exponential (Gaussian) form factors are also widely adopted in literature. We have checked and determined that a monopole type of the form factor will result in a significantly bigger
$ \chi^2 $ , thus indicting a substantially worse fitting quality, while an exponential (Gaussian) type of form factor will result in similar results as those presented in this paper, although the model parameters change negligibly. -
As mentioned in the introduction section of this paper, very recently, the first data on total cross sections for the
$ \gamma p \to K^+ \Lambda(1690) $ reaction became available from the CLAS Collaboration [35]. In this work, for the first time, we perform a theoretical analysis of these data within an effective Lagrangian approach. We construct the reaction amplitudes by including the t-channel K and$ K^\ast $ exchanges, the s-channel nucleon and nucleon resonance exchanges, and the interaction current. The gauge invariance of the photoproduction amplitudes is fully implemented by introducing an auxiliary current in the generalized contact term (cf. Eq. (2)). As the data for$ \gamma p \to $ $ K^+ \Lambda(1690) $ are scarce, the strategy adopted in the present work for introducing nucleon resonances is that we introduce nucleon resonances as few as possible to describe the available data.First, we attempt to observe how the total cross-section data of the
$ \gamma p\to K^+\Lambda(1690) $ reaction [35] can be described without introducing any nucleon resonance. In Fig. 2, we present the results obtained from the Born amplitudes with the green dashed line. Evidently, the Born amplitudes themselves are far from sufficient in describing the data, thus indicating the necessity of the contributions from the resonance exchanges.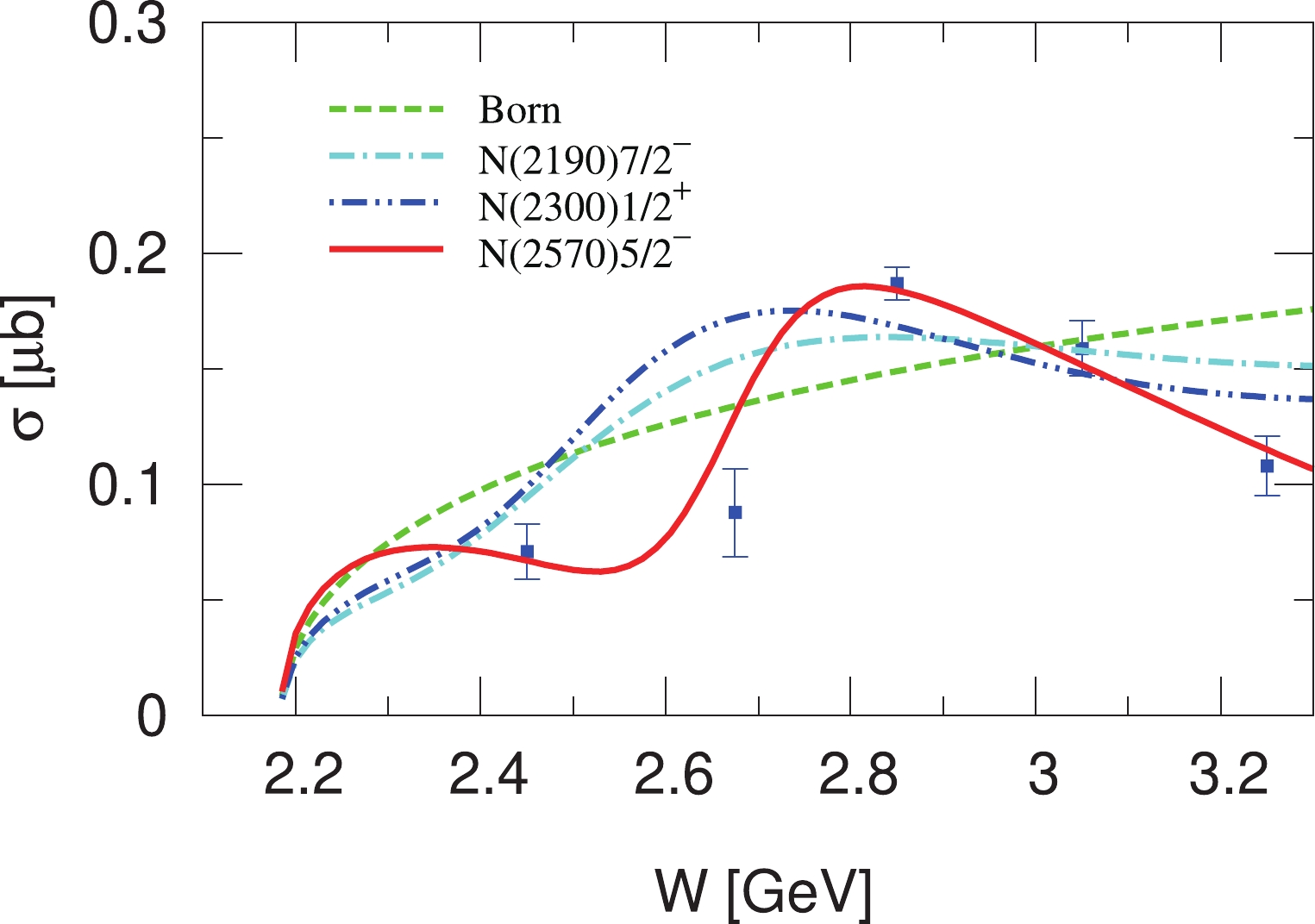
Figure 2. (color online) Total cross sections for
$ \gamma p\to K^+\Lambda(1690) $ . The green dashed line represents the results without any nucleon resonance. The cyan dot-dashed, blue double-dot-dashed, and red solid lines denote the results obtained by including the$ N(2190)7/2^- $ ,$ N(2300)1/2^+ $ , and$ N(2570)5/2^- $ resonances in the s channel, respectively. Data are taken from the CLAS Collaboration [35].In RPP [1], there are three nucleon resonances lying above the threshold of the
$ \gamma p\to K^+\Lambda(1690) $ reaction with spin$ J \leq 7/2 $ , namely, the$ N(2190)7/2^- $ ,$ N(2300)1/2^+ $ , and$ N(2570)5/2^- $ resonances①. Subsequently, we attempt to include one of them in the s-channel, to describe the data. We adopt Minuit to fit the model parameters, and the resulted$ \chi^2 $ per data are$ 7.69 $ ,$ 7.64 $ , and$ 1.17 $ , respectively, for results including each of the$ N(2190)7/2^- $ ,$ N(2300)1/2^+ $ , and$ N(2570)5/2^- $ resonances. The corresponding results are shown in Fig. 2, where the cyan dot-dashed, blue double-dot-dashed, and red solid lines denote the results obtained by including the$ N(2190)7/2^- $ ,$ N(2300)1/2^+ $ , and$ N(2570)5/2^- $ resonances in the s channel, respectively. Evidently, although the fits with the$ N(2190)7/2^- $ and$ N(2300)1/2^+ $ resonances fail to reproduce the data, the fit with the$ N(2570)5/2^- $ resonance describes the data satisfactorily well.In the remainder of this section, we present a detailed discussion of the model results for the
$ \gamma p\to K^+\Lambda(1690) $ reaction obtained by including the$ N(2570)5/2^- $ resonance. In Table 1, we present the fitted values of the corresponding model parameters. For resonance couplings, we present the reduced helicity amplitudes$ \sqrt{\beta_{\Lambda^\ast K}}A_j $ , instead of showing their strong and electromagnetic coupling constants separately [30, 36, 44, 45, 51], because in tree-level calculations, as performed in this work, only the products of the resonance strongnic and electromagnetic coupling constants are relevant to the reaction amplitudes. Here$ \beta_{\Lambda^\ast K} $ is the branching ratio for the resonance decay to$ \Lambda(1690) K $ , and$ A_j $ is the helicity amplitude with spin j ($ j = 1/2,3/2 $ ) for resonance radiative decay to$ \gamma p $ . The values in the brackets below the mass$ M_R $ and width$ \Gamma_R $ of the resonance$ N(2570){5/2}^- $ are the corresponding values listed in RPP [1], which are quoted from the results of BESIII [52]. One can see that both the fitted mass and width for the resonance$ N(2570)5/2^- $ are close to the ranges given by BESIII [52].Parameter Values $\Lambda_{\rm{bg} } /{\rm{MeV} }$ 

$ 965 \pm 16 $ 

$ g_{\Lambda^\ast N K^\ast} $ 

$ -19.32 \pm 14.76 $ 

$ N(2570){5/2}^- $ 

$ \ast \ast $ 

$M_R /{\rm{MeV} }$ 

$ 2660 \pm 5 $ 

[ $ 2570^{+19+34}_{-10-10} $ ]

$\Gamma_R /{\rm{MeV} }$ 

$ 300 \pm 16 $ 

[ $ 250^{+14+69}_{-24-21} $ ]

$\Lambda_{R} /{\rm{MeV} }$ 

$ 2390 \pm 82 $ 

$\sqrt{\beta_{\Lambda^\ast K} }A_{1/2} /(10^{-3}\,{\rm{GeV} }^{-1/2})$ 

$ -4.61 \pm 0.06 $ 

$\sqrt{\beta_{\Lambda^\ast K} }A_{3/2} /(10^{-3}\,{\rm{GeV} }^{-1/2})$ 

$ 6.24 \pm 0.23 $ 

Table 1. Fitted values of model parameters. The asterisks below the resonance
$ N(2570){5/2}^- $ denote the overall status of this resonance evaluated by RPP [1]. The values in the brackets below the mass$ M_R $ and width$ \Gamma_R $ of the resonance$ N(2570){5/2}^- $ are the corresponding values listed in RPP [1], which are quoted from the results of BESIII [52].$ \sqrt{\beta_{\Lambda^\ast K}}A_{j} $ is the reduced helicity amplitude for resonance$ N(2570)5/2^- $ with$ \beta_{\Lambda^\ast K} $ denoting the branching ratio of the resonance decay to$ \Lambda(1690) K $ and$ A_{j} $ denoting the helicity amplitude with spin j for resonance radiative decay to$ \gamma p $ .In Fig. 3, the model results of the total cross sections (the red solid line) for the
$ \gamma p\to K^+\Lambda(1690) $ reaction are shown and compared to the corresponding data from the CLAS Collaboration [35]. The contributions calculated from each individual reaction amplitudes are also shown with the cyan dot-dashed, blue double-dot-dashed, green dashed, blue double-dotted, and magenta dotted lines representing the contributions from the individual amplitudes of the interaction current, s-channel$ N(2570)5/2^- $ exchange, t-channel$ K^\ast $ exchange, t-channel K exchange, and s-channel N exchange, respectively. Evidently, near the threshold, the interaction current dominates the$ \gamma p \to K^+ \Lambda(1690) $ reaction as a consequence of gauge invariance. The t-channel K exchange makes considerable contributions to the$ \gamma p \to K^+ \Lambda(1690) $ reaction and its destructive interference with the interaction current is observed. The contributions from the t-channel$ K^\ast $ exchange, as well as the s-channel nucleon exchange, are very small. The$ N(2570)5/2^- $ resonance exchange provides significant contributions at high energies, and actually, its constructive interference with the interaction current is responsible for the bump structure shown in the CLAS total cross-section data at the center-of-mass energies above$ W \approx 2.7 $ GeV.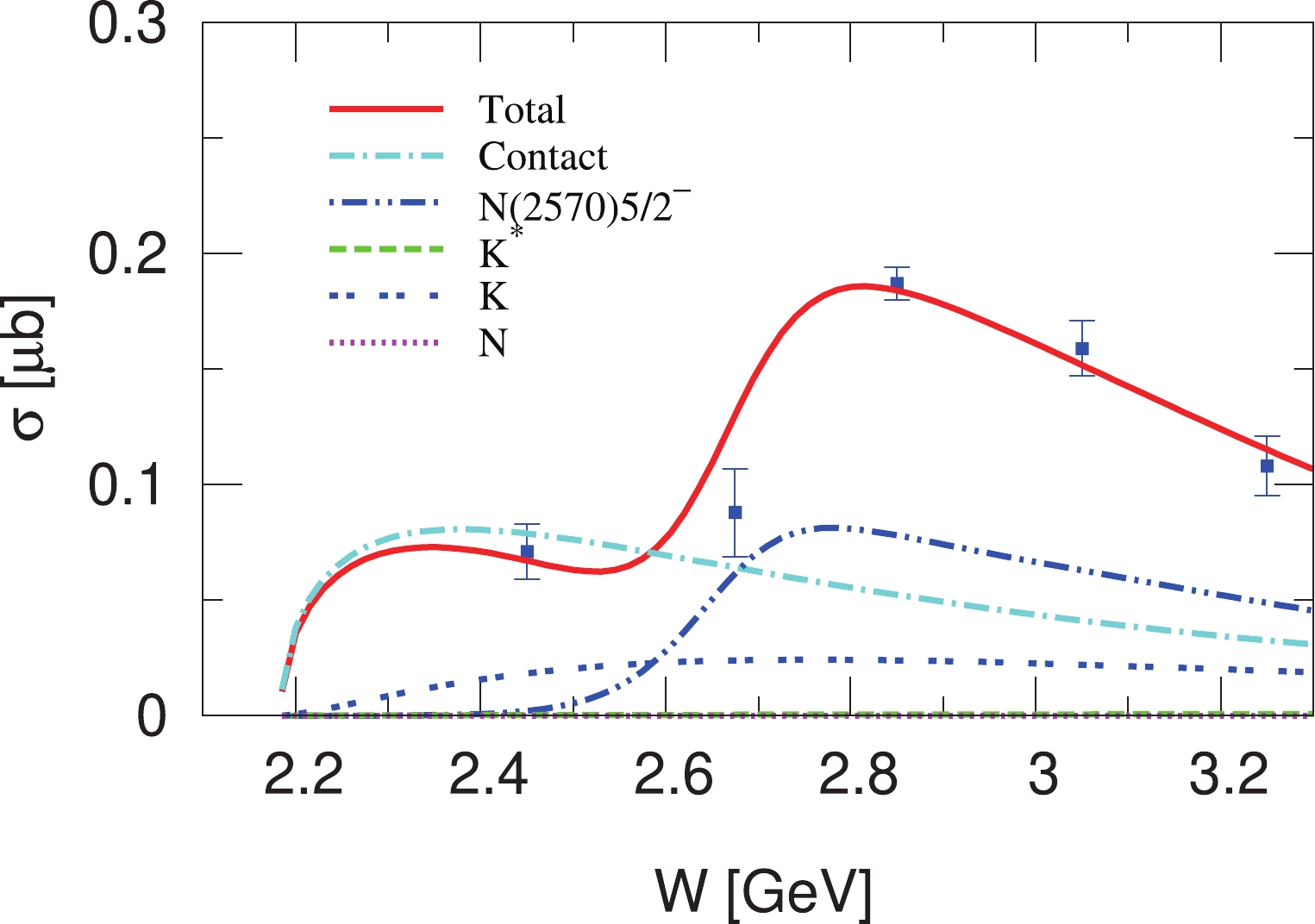
Figure 3. (color online) Total cross sections for
$ \gamma p\to K^+\Lambda(1690) $ . The red solid line denotes the results obtained by the full reaction amplitude with the$ N(2570)5/2^- $ resonance. The cyan dot-dashed, blue double-dot-dashed, green dashed, blue double-dotted, and magenta dotted lines represent the results from the individual contributions of the interaction current, s-channel$ N(2570)5/2^- $ exchange, t-channel$ K^\ast $ exchange, t-channel K exchange, and s-channel N exchange, respectively. Data are taken from the CLAS Collaboration [35].In Fig. 4, we show the predictions of the differential cross sections for
$ \gamma p\to K^+\Lambda(1690) $ from the present model. The contributions from individual interaction diagrams are also presented in this figure. Evidently, at the lower energy region, the interaction current dominates the differential cross sections of this reaction and has destructive interference with the t-channel K exchange, which contributes mainly at the forward angles. Note that, the dominance of the interaction current is also observed in the$ \gamma p \to K^+\Lambda(1520) $ reaction [25, 26, 28, 30]. As energy increases, the contributions from the s-channel$ N(2570)5/2^- $ exchange become prominent. These predicted differential cross sections for the$ \gamma p\to K^+\Lambda(1690) $ reaction provide theoretical guidance for the experimental measurements and can be tested by the future data.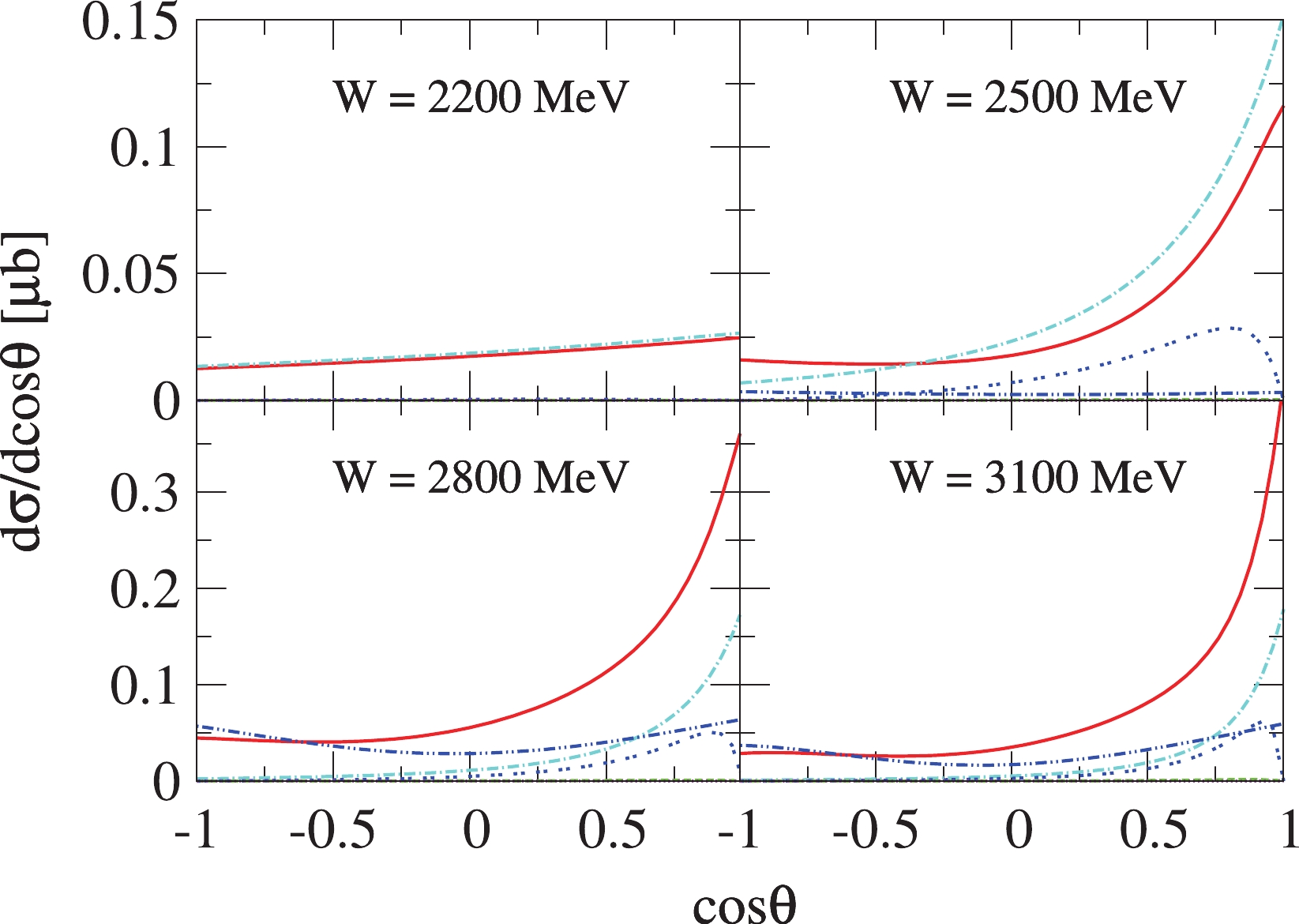
Figure 4. (color online) Predicted differential cross sections for
$ \gamma p\to K^+\Lambda(1690) $ at four selected energies. The red solid lines denote the results obtained by the full reaction amplitudes with the$ N(2570)5/2^- $ resonance. The cyan dot-dashed, blue double-dot-dashed, green dashed, blue double-dotted, and magenta dotted lines represent the individual contributions from the interaction current, s-channel$ N(2570)5/2^- $ exchange, t-channel$ K^\ast $ exchange, t-channel K exchange, and s-channel N exchange, respectively. -
The first measurement of the total cross sections for the
$ \gamma p \to K^+ \Lambda(1690) $ reaction was presented most recently by the CLAS Collaboration in Ref. [35]. In this study, for the first time, we performed a theoretical analysis on these data within an effective Lagrangian approach. In addition to the s-channel nucleon exchange, t-channel K and$ K^\ast $ exchanges, and generalized interaction current, we considered as few as possible nucleon resonance exchanges in the s channel in constructing the reaction amplitudes for$ \gamma p \to K^+ \Lambda(1690) $ , to describe the data. The gauge invariance of the full photoproduction amplitude was fully implemented by considering a particular auxiliary current in the generalized interaction current (cf. Eqs. (2) and (5)).It was found that the available total cross-section data for the
$ \gamma p \to K^+ \Lambda(1690) $ reaction can be satisfactorily described by introducing the s-channel$ N(2570)5/2^- $ exchange. The fitted mass and width for$ N(2570)5/2^- $ are close to the ranges listed in RPP [1], which are quoted from the results of BESIII [52]. The interaction current was found to dominate the cross sections of$ \gamma p \to $ $ K^+ \Lambda(1690) $ near the reaction threshold. Considerable contributions from the t-channel K exchange were observed. The t-channel$ K^\ast $ exchange and s-channel nucleon exchange were found to make rather small contributions to the cross sections of$ \gamma p \to K^+ \Lambda(1690) $ . The$ N(2570)5/2^- $ resonance exchange provides significant contributions at high energies, and its constructive interference with the interaction current was inferred to be responsible for the bump structure shown in the CLAS total cross-section data at the center-of-mass energies above$ W \approx 2.7 $ GeV. The differential cross sections for the$ \gamma p \to K^+ \Lambda(1690) $ reaction were predicted, which provide theoretical guidance for future experiments.
Photoproduction ${ \boldsymbol\gamma \boldsymbol p \boldsymbol \to {\boldsymbol K}^+\boldsymbol\Lambda{\boldsymbol{(1690)}} }$ in an effective Lagrangian approach
- Received Date: 2021-10-04
- Available Online: 2022-05-15
Abstract: A gauge-invariant model is constructed for the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: