-
The effect of strong external magnetic fields in non-central heavy-ion collisions (HICs) is a popular area of research [1-8]. The presence of temperature and isospin asymmetry, i.e., uneven numbers of neutrons and protons, results in significant modifications to the in-medium properties of hadrons [6, 9, 10]. Strong magnetic fields of the order of
$ eB\sim {15{m^2_{\pi}}} $ ($ 5\times 10^{19} $ gauss) at the Large Hadron Collider (LHC), CERN, and$ eB\sim {2{m^2_{\pi}}} $ ($ 6.5\times 10^{18} $ gauss) at the Relativistic Heavy Ion Collider (RHIC), BNL, might have been produced [1-3]. In non-central ultra-relativistic heavy-ion collisions, as matter moves away from collision zone, the strength of the magnetic field rapidly decays. However, it is believed that the interaction of the magnetic field with residual matter results in induced currents; following Lenz's law, the induced magnetic field is produced along the direction of the external magnetic field. The induced currents modify the electrical conductivity of the medium; therefore, the relaxation (decay) time of the external magnetic field increases [4, 6, 11-15]. A high electrical conductivity of the medium was anticipated near the critical temperature$ T_c $ [16]. The high electrical conductivity suggests the sustainability of the external magnetic field in a thermalized hadronic regime; therefore, the in-medium properties of η mesons may alter under the influence of the magnetic field. The time evolution of the external magnetic field in heavy-ion collisions is still unclear, and accurate estimations of the relaxation time are expected from the solutions of the magnetohydrodynamics equations.In the future experiments, such as compressed baryonic matter (CBM) and antiproton annihilation at Darmstadt (PANDA) at GSI, Germany, the Japan Proton Accelerator Research Complex (J-PARC) in Japan, and the Nuclotron-based Ion Collider Facility (NICA) in Dubna, Russia, we anticipate significant research on in-medium meson-baryon interactions [17-19]. On the theoretical side, various effective models have been built to study the dynamics of the non-perturbative regime. These models include the quark-meson coupling (QMC) model [20-25], the Polyakov quark meson (PQM) model [26, 27], the coupled channel approach [28-31], the chiral SU(3) model [9, 10, 18, 32, 33], chiral perturbation theory (ChPT) [34-36], QCD sum rules [37-42], the Nambu-Jona-Lasinio (NJL) model [43], and the Polyakov loop extended NJL (PNJL) model [44-46]. The Dyson-Schwinger equation is another method of studying the in-medium properties of mesons under the influence of a uniform homogeneous magnetic field at finite chemical potential and temperature. In this approach, the magnetically modified propagator is utilized to calculate the self-energy of pions in one loop [47]. In the current study, we used two of the above theoretical approaches: the chiral SU(3) model and ChPT.
Interest in the in-medium study of η mesons originates from attractive
$ \eta N $ interactions. The expectation of negative$ \eta N $ interactions suggested the possible formation of eta-mesic nuclei [48-50]. From η photo production on a deutron, Sibirtsev et al. anticipated$ a^{\eta N} $ = 0.42+i 0.34 fm, which supports the weak system of eta-mesic nuclei [51]. The properties of η mesons, [52-57], for instance, the transverse momentum spectrum near the threshold of free N-N production [54] and η-meson production, have been studied experimentally [52-54]. On the theoretical side, Haider and Liu were the first to observe that$ \eta N $ interactions exhibit an attractive behavior and therefore the η-meson can form a bound state with nucleons [48, 49]. Chiang$et\ al.$ anticipated an optical potential$ U_{\eta} $ = −34 MeV at$ \rho_0 $ using the chiral coupled channel approach [58]. It was also predicted that the negative potential can be used to generate a η-mesic atom with a light/heavy nucleus. At the nuclear saturation density$ \rho_0 $ , by incorporating the leading order terms in the coupled channel approach, a mass-shift of −20 MeV was evaluated [50]. In Ref. [59], an optical potential of −72 MeV was anticipated. Moreover, an optical potential of −60 MeV was predicted at$ \rho_{N} = \rho_0 $ using the QMC model [60]. Using ChPT and the relativistic mean-field model at the nuclear saturation density with the$ \eta N $ off-shell terms in the equation of motion, Ref. [35] anticipated an optical potential of −83$ \pm $ 5 MeV [35]. Furthermore, using the same approach, Song$ et $ $ al. $ obtained a negative optical potential as a function of the$ \eta N $ scattering length [61]. Chen et al. studied the η production rate and momentum dependence under the influence of isospin asymmetric HICs in Ref. [62], and the effect of$ \eta N $ interactions was also studied using the intranuclear cascade model under the influence of distinct medium characteristics [63]. Recently, using the combined (chiral SU(3) model$ + $ ChPT) and solo (chiral SU(3) model) approaches, we derived an$ \eta N $ equation of motion in non-magnetized nuclear matter and observed a (−54.61) −116.83 MeV mass-shift at$ \rho_0 $ with$ a^{\eta N} $ = 1.02 fm [36]. Evidently, the mass and optical potential of η-mesons have model dependencies and therefore require further exploration.In this study, we investigated the magnetic field effect on the in-medium mass and optical potential of η-mesons in hot asymmetric nuclear matter; we extended upon our previous study on the nuclear medium at zero magnetic field [36]. First, we evaluated the in-medium dispersion relation of η-mesons using the
$ \eta N $ Lagrangian from the magnetically induced scalar densities in the chiral SU(3) model [36]. In the second approach, we used the scalar density of nucleons calculated using the chiral SU(3) model in the dispersion relation of η-mesons, which is derived from the chiral effective$ \eta N $ Lagrangian of chiral perturbation theory [35].Chiral perturbation theory is widely used to study in-medium baryon-meson interactions. This theory was first used to investigate the in-medium properties of kaons [64], and later it was modified by introducing leading order terms in the Lagrangian to study the interactions between η and nucleons [34]. The theory was also used to study astrophysical objects, such as neutron stars; for neutron star matter, heavy baryon ChPT was applied to study kaon condensation [65-67]. Furthermore, to provide a correct description of
$ \eta N $ interactions, next-to-leading order terms were introduced in the ChPT Lagrangian. Consequently, a deeper η-meson optical potential was anticipated in the nuclear medium [35]. Additionally, the chiral SU(3) model is widely used to study hot and dense hadronic matter [32, 68, 69]. For instance, this methodology was used for strange hadronic matter to study the in-medium properties of kaons and antikaons [69]. Recently, the mass and decay width of the ϕ meson was calculated in strange hadronic matter by considering the$ K {\bar {K}} $ loop at the one-loop level [70]. The chiral SU(3) model was extended to the charm SU(4) and bottom SU(5) sectors to study the properties of heavy D and B mesons, respectively [10, 33, 71]. Moreover, the chiral model is successfully used to anticipate the in-medium properties of baryons and mesons in the presence of a strong external magnetic field. For instance, using the combined chiral model and QCD sum rule approach, the in-medium mass and decay constant of scalar, pseudoscalar, vector, and axial-vector D mesons were calculated with [19, 72] and without incorporating the influence of the external magnetic field [73-76]. Using the same combination, the medium modified properties of charmonia and bottomonia were studied in hot magnetized asymmetric nuclear matter [18, 32, 77].The outline of this paper is as follows. In the subsequent section, we will provide a brief explanation on the magnetic field effect observed in this study. In Section II.A.1, we will derive the magnetically induced
$ \eta N $ interactions in the chiral SU(3) model, whereas Section II.A.2, contains the$ \eta N $ formalism for the joint chiral model and chiral perturbation theory approach. In Section III, we will discuss the in-medium effects of a strong magnetic field on the mass of η-mesons. Finally, in Section IV, we will conclude our investigation. -
The hadronic chiral SU(3) model incorporates the trace anomaly and non-linear realization of the chiral symmetry [9, 18, 72, 78-81] property of QCD. In this methodology, η-nucleon interactions are computed via the exchange of scalar (σ, ζ, δ and χ) and vector (ω and ρ) fields. The glueball field χ is introduced in the model to preserve the broken scale invariance property of QCD [72]. The isospin asymmetry, I, of nuclear matter is introduced through the addition of the scalar-isovector field δ and vector-isovector field ρ [32]. In the present study, the impact of the strong magnetic field along the Z-axis with the vector potential
$ A^\mu = (0,0,Bx,0) $ is studied by including the magnetically induced Lagrangian density in the effective Lagrangian density of the chiral model [6, 18]. Thus, we express the modified Lagrangian density of chiral model as$ {\cal{L}}_{\rm chiral} = {\cal{L}}_{\rm kin} + \sum\limits_{ M = S,V}{\cal{L}}_{\rm NM} + {\cal{L}}_{\rm vec} + {\cal{L}}_0 + {\cal{L}}_{\rm SB}+{\cal{L}}_{\rm mag}. $

(1) Individually,
$ {\cal{L}}_{\rm NM} = - \sum\limits_{i} \bar {\psi_i} \left[ m_{i}^{*} + g_{\omega i} \gamma_{0} \omega + g_{\rho i} \gamma_{0} \rho \right] \psi_{i}, $

(2) $ {\cal{L}} _{\rm vec} =\frac {1}{2} \left( m_{\omega}^{2} \omega^{2} + m_{\rho}^{2} \rho^{2} \right) \frac {\chi^{2}}{\chi_{0}^{2}} + g_4 (\omega ^4 +6\omega^2 \rho^2+\rho^4), $

(3) $\begin{aligned}[b] {\cal{L}} _{0} = & -\frac{1}{2} k_{0}\chi^{2} \left( \sigma^{2} + \zeta^{2} + \delta^{2} \right) + k_{1} \left( \sigma^{2} + \zeta^{2} + \delta^{2} \right)^{2} \\ &+ k_{2} \left( \frac {\sigma^{4}}{2} + \frac {\delta^{4}}{2} + 3 \sigma^{2} \delta^{2} + \zeta^{4} \right) + k_{3}\chi\left( \sigma^{2} - \delta^{2} \right)\zeta \\ &- k_{4} \chi^{4} - \frac {1}{4} \chi^{4} {\rm {ln}} \frac{\chi^{4}}{\chi_{0}^{4}} + \frac {d}{3} \chi^{4} {\rm {ln}} \Bigg (\Bigg( \frac {\left( \sigma^{2} - \delta^{2}\right) \zeta }{\sigma_{0}^{2} \zeta_{0}} \Bigg) \bigg (\frac {\chi}{\chi_0}\bigg)^3 \Bigg ), \end{aligned} $

(4) $ {\cal{L}} _{\rm SB} = -\left( \frac {\chi}{\chi_{0}}\right)^{2} \left[ m_{\pi}^{2} f_{\pi} \sigma + \big( \sqrt {2} m_{K}^{2}f_{K} - \frac {1}{\sqrt {2}} m_{\pi}^{2} f_{\pi} \big) \zeta \right], $

(5) and
$ {\cal{L}}_{\rm mag} = -{\bar {\psi_i}}q_i \gamma_\mu A^\mu \psi_i -\frac {1}{4} \kappa_i \mu_N {\bar {\psi_i}} \sigma ^{\mu \nu}F^{\mu \nu} \psi_i -\frac{1}{4} F^{\mu \nu} F_{\mu \nu}. $

(6) In Eq. (1), the first term
${\cal{L}}_{\rm kin}$ denotes the kinetic energy term, and the second term${\cal{L}}_{\rm NM}$ , given by Eq. (2), represents the nucleon-meson interaction term. In this equation, the in-medium mass of nucleons is given as$ m_{i}^{*} = -(g_{\sigma i}\sigma + g_{\zeta i}\zeta + g_{\delta i}\tau_3 \delta) $ where$ \tau_3 $ denotes the zth component of the isospin quantum number and$ g_{\sigma i} $ ,$ g_{\zeta i} $ , and$ g_{\delta i} $ denote the coupling strengths of the scalar-isoscalar field σ, scalar-isoscalar field ζ, and scalar-isovector field δ with nucleons (i =$ p,n $ ), respectively. The term${\cal{L}}_{\rm vec}$ (Eq. (3)) generates the mass of the vector mesons through interactions with scalar mesons and quartic self-interaction terms, and$ {\cal{L}}_{0} $ represents spontaneous chiral symmetry breaking, where$ \sigma_0 $ ,$ \zeta_0 $ ,$ \delta_0 $ , and$ \chi_0 $ symbolize the vacuum values of the σ, ζ, δ, and χ scalar fields, respectively. To calculate the value of the d parameter in the final term of Eq. (4), we recall that the QCD β function at the one loop level for$ N_{c} $ colors and$ N_{f} $ flavours is given by [82, 83]$ \beta_{\rm {QCD}} \left( g \right) = -\frac{11 N_{c} g^{3}}{48 \pi^{2}} + \frac{ N_{f} g^{3}}{24 \pi^{2}} + O(g^{5}). $

(7) In the above expression, the first term originates from gluon self-interaction (anti-screening) and the second term from interactions between quark pairs (screening). For
$ N_c $ = 3 and$ N_f $ = 3, we estimate the value of d to be 6/33, whereas for$ N_c $ = 3 and$ N_f $ = 2, the parameter d gives the value 4/33 [32, 82, 83]. In the present model, we use d = 0.064 [32], which is fitted along with other medium parameters, such as$ k_i(i = 1 $ to$ 4) $ , to generate the vacuum values of fields ($ \sigma_0 $ ,$ \zeta_0 $ ,$ \delta_0 $ ,$ \chi_0 $ ,$ \omega_0 $ , and$ \rho_0 $ ) and the masses of the nucleons and η,$ \eta' $ mesons [9, 18, 32]. The values of the fitted medium parameters are listed in Table 1.Parameter Value Parameter Value Parameter Value $k_0$ 

2.53 $\sigma_0$ /MeV

−93.29 $g_{\sigma N}$ 

10.56 $k_1$ 

1.35 $\zeta_0$ /MeV

−106.8 $g_{\zeta N }$ 

−0.46 $k_2$ 

−4.77 $\chi_0$ /MeV

409.8 $g_{\delta N }$ 

2.48 $k_3$ 

−2.77 d 0.064 $g_{\omega N}$ 

13.35 $k_4$ 

−0.218 $g_4$ 

79.91 $g_{\rho N}$ 

5.48 $f_K$ /MeV

122.14 $\rho_0$ /

${\mathrm{fm} }^{-3}$ 

0.15 $m_{\sigma}$ /MeV

466.5 $m_\pi $ /MeV

139 $ m_K$ /MeV

494 $ f_\pi$ /MeV

93.29 $m_{\zeta}$ /MeV

1024.5 $m_{\delta}$ /MeV

899.5 $m_{\eta}$ /MeV

574.374 $M_N$ /MeV

939 Table 1. Values of different parameters used in the present investigation [9].
Furthermore,
${\cal{L}}_{\rm SB}$ in Eq. (5) denotes the explicit chiral symmetry breaking property. The term${\cal{L}}_{\rm mag}$ accounts for hadron interaction with the magnetic field. In Eq. (6), the symbol$ \psi_i $ represents the wave function of the ith nucleon, and the second term describes the tensorial interaction with the electromagnetic tensor,$ F_{\mu \nu} $ . Moreover, the symbols$ \mu_N $ and$ k_i $ represent the nuclear magneton ($ \mu_N $ =$ \dfrac{e}{2m_N} $ ) and anomalous magnetic moment of the ith nucleon, respectively.The non-linear coupled equations of motion for meson fields are obtained by solving the Euler-Lagrange equations using the total Lagrangian [Eq. (1)] [18, 77] and are given as
$ \begin{aligned}[b] k_{0}\chi^{2}\sigma&-4k_{1}\left( \sigma^{2}+\zeta^{2} +\delta^{2}\right)\sigma-2k_{2}\left( \sigma^{3}+3\sigma\delta^{2}\right) -2k_{3}\chi\sigma\zeta \\& -\frac{d}{3} \chi^{4} \bigg (\frac{2\sigma}{\sigma^{2}-\delta^{2}}\bigg ) +\left( \frac{\chi}{\chi_{0}}\right) ^{2}m_{\pi}^{2}f_{\pi} = \sum g_{\sigma i}\rho_{i}^{s} , \end{aligned} $

(8) $ \begin{aligned}[b] k_{0}\chi^{2}\zeta&-4k_{1}\left( \sigma^{2}+\zeta^{2}+\delta^{2}\right) \zeta-4k_{2}\zeta^{3}-k_{3}\chi\left( \sigma^{2}-\delta^{2}\right)\\& -\frac{d}{3}\frac{\chi^{4}}{\zeta}+\left(\frac{\chi}{\chi_{0}} \right) ^{2}\left[ \sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi}^{2}f_{\pi}\right] = \sum g_{\zeta i}\rho_{i}^{s} , \end{aligned} $

(9) $ \begin{aligned}[b] k_{0}\chi^{2}\delta&-4k_{1}\left( \sigma^{2}+\zeta^{2}+\delta^{2}\right) \delta-2k_{2}\left( \delta^{3}+3\sigma^{2}\delta\right) +2k_{3}\chi\delta \zeta \\ & + \frac{2}{3} d \chi^4 \left( \frac{\delta}{\sigma^{2}-\delta^{2}}\right) = \sum g_{\delta i}\tau_3\rho_{i}^{s} , \end{aligned} $

(10) $ \left (\frac{\chi}{\chi_{0}}\right) ^{2}m_{\omega}^{2}\omega+g_{4}\left(4{\omega}^{3}+12{\rho}^2{\omega}\right) = \sum g_{\omega i}\rho_{i}^{v} , $

(11) $ \left (\frac{\chi}{\chi_{0}}\right) ^{2}m_{\rho}^{2}\rho+g_{4}\left(4{\rho}^{3}+12{\omega}^2{\rho}\right) = \sum g_{\rho i}\tau_3\rho_{i}^{v} , $

(12) and
$ \begin{aligned}[b]\\[-8pt]& k_{0}\chi \left( \sigma^{2}+\zeta^{2}+\delta^{2}\right)-k_{3} \left( \sigma^{2}-\delta^{2}\right)\zeta + \chi^{3}\left[1 +{\rm {ln}}\left( \frac{\chi^{4}}{\chi_{0}^{4}}\right) \right] +(4k_{4}-d)\chi^{3} -\frac{4}{3} d \chi^{3} {\rm {ln}} \Bigg ( \bigg (\frac{\left( \sigma^{2} -\delta^{2}\right) \zeta}{\sigma_{0}^{2}\zeta_{0}} \bigg ) \bigg (\frac{\chi}{\chi_0}\bigg)^3 \Bigg )\\&\quad+ \frac{2\chi}{\chi_{0}^{2}}\left[ m_{\pi}^{2} f_{\pi}\sigma +\left(\sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi}^{2}f_{\pi} \right) \zeta\right] -\frac{\chi}{{{\chi_0}^2}}(m_{\omega}^{2} \omega^2+m_{\rho}^{2}\rho^2) = 0 , \end{aligned} $ 
(13) respectively.
In the above equations, the symbols
$ m_\pi $ ,$ m_K $ ,$ f_\pi $ , and$ f_K $ represent the masses and decay constants of pions and kaons, respectively. The isospin effect is measured by the parameters through the definition,$ I = -\dfrac{\Sigma_i \tau_{3i} \rho^{v}_{i}}{2\rho_{N}} $ . Furthermore,$ \rho^{s}_{i} $ and$ \rho^{v}_{i} $ describe the magnetic field induced scalar and vector densities of the ith nucleons ($ i = n,p $ ) [18, 84, 85]. Due to Landau quantization, the magnetic field interacts with protons and neutrons differently. For an uncharged neutron, the expressions for scalar and vector densities are given as$ \begin{aligned}[b] \rho^{s}_{n} =& \frac{1}{2\pi^{2}}\sum\limits_{s = \pm 1}\int^{\infty}_{0} k^{n}_{\bot}{\rm d}k^{n}_{\bot}\left(1-\frac{s\mu_{N}\kappa_{n}B} {\sqrt{m^{* 2}_{n}+\left(k^{n}_{\bot}\right)^{2}}} \right) \\&\times \int^{\infty}_{0}\, {\rm d}k^{n}_{\parallel} \frac{m^*_n}{\tilde E^{n}_{s}}\left( f^n_{k, s}+\bar{f}^n_{k, s}\right), \end{aligned} $

(14) and
$ \rho^{v}_{n} = \frac{1}{2\pi^{2}}\sum\limits_{s = \pm 1}\int^{\infty}_{0}k^{n}_{\bot} {\rm d}k^{n}_{\bot} \int^{\infty}_{0}\, {\rm d}k^{n}_{\parallel} \left( f^n_{k, s}-\bar{f}^n_{k, s}\right), $

(15) respectively. Likewise, the scalar and vector densities for a charged proton with the effect of Landau quantization are given by [84, 85]
$ \begin{aligned}[b] \rho^{s}_{p} =& \frac{|q_{p}|Bm^{*}_{p}}{2\pi^2} \Bigg [ \sum\limits_{\nu = 0}^{\nu_{\max}^{(s = 1)}}\int^{\infty}_{0}\frac{{\rm d}k^p_{\parallel}}{\sqrt{(k^{p}_{\parallel})^2 +(\bar m_{p})^2}}\left( f^p_{k,\nu, s}+\bar{f}^p_{k, \nu, s}\right) \\&+\sum\limits_{\nu = 1}^{\nu_{\max}^{(s = -1)}} \int^{\infty}_{0}\frac{{\rm d}k^p_{\parallel}}{\sqrt{(k^{p}_{\parallel})^2 +(\bar m_{p})^2}}\left( f^p_{k,\nu, s}+\bar{f}^p_{k, \nu, s}\right) \Bigg], \end{aligned} $

(16) and
$ \begin{aligned}[b] \rho^{v}_{p} =& \frac{|q_{p}|B}{2\pi^2} \Bigg [ \sum\limits_{\nu = 0}^{\nu_{\max}^{(s = 1)}} \int^{\infty}_{0} {\rm d}k^p_{\parallel}\left( f^p_{k,\nu, s}-\bar{f}^p_{k,\nu, s}\right) \\&+\sum\limits_{\nu = 1}^{\nu_{\max}^{(s = -1)}} \int^{\infty}_{0} {\rm d}k^p_{\parallel}\left( f^p_{k,\nu, s}-\bar{f}^p_{k,\nu, s}\right) \Bigg], \end{aligned} $

(17) respectively.
In the above equations,
$ \bar m_{p} $ =$ \sqrt{m^{* 2}_{p}+2\nu |q_{p}|B}-s\mu_{N}\kappa_{p}B $ defines the effective mass of the proton, where the symbol$ \nu $ represents the Landau levels. The effective energy of neutrons and protons is given by$ \tilde E^{n}_{s} = \sqrt{\left(k^{n}_{\parallel}\right)^{2} + \left(\sqrt{m^{* 2}_{n}+\left(k^{n}_{\bot}\right)^{2} }-s\mu_{N}\kappa_{n}B \right)^{2}}, $

(18) and
$ \tilde E^{p}_{\nu, s} = \sqrt{\left(k^{p}_{\parallel}\right)^{2}+ \left(\sqrt{m^{* 2}_{p}+2\nu |q_{p}|B}-s\mu_{N}\kappa_{p}B \right)^{2}}, $

(19) respectively. In addition, the symbols
$ {f}^n_{k, \nu, s} $ ,$ \bar{f}^n_{k, \nu, s} $ ,$ {f}^p_{k, s} $ , and$ \bar{f}^p_{k, s} $ define the finite temperature Fermi distribution functions for nucleons and their antinucleons and are given as$\begin{aligned}[b] &f^n_{k, s} = \frac{1}{1+\exp\left[\beta(\tilde E^n_{s} -\mu^{*}_{n}) \right]},\\ & \bar{f}^n_{k, s} = \frac{1}{1+\exp\left[\beta(\tilde E^n_{s} +\mu^{*}_{n} )\right]}. \end{aligned}$

(20) $\begin{aligned}[b]&f^p_{k,\nu, s} = \frac{1}{1+\exp\left[\beta(\tilde E^p_{\nu, s} -\mu^{*}_{p}) \right]}, \\& \bar{f}^p_{k,\nu, s} = \frac{1}{1+\exp\left[\beta(\tilde E^p_{\nu, s} +\mu^{*}_{p} )\right]}. \end{aligned} $

(21) -
In this subsection, we evaluate the in-medium mass of η mesons via a dispersion relation in hot magnetized asymmetric nuclear matter. The medium modified η meson mass is obtained in terms of the scalar and vector fields of the chiral model, which are solved by considering the interactions of nucleons with η mesons in the presence of an external magnetic field. These scalar and vector fields modify the scalar and vector densities of the nucleons, which consequently modifies the self-energy of the η mesons.
The
$ \eta N $ interaction Lagrangian is given as$ {\mathcal L}_{{\eta N}} = {\mathcal L}_{{\rm RT}}+ {\cal{L}}_{\eta\rm SB} + {\cal{L }}_{d_1}^{\rm BM}+ {\cal{L }}_{d_2}^{\rm BM}. $

(22) The individual terms are given in detail, as follows:
$1.$ ${\mathcal L}_{{\rm RT}}$ , the first range term:The first term in the
$ \eta N $ Lagrangian arises from the first range term$ {\mathcal L}_{{\mathrm{1st range term}}} = {\rm Tr} (u_{\mu} X u^{\mu}X +X u_{\mu} u^{\mu} X) , $

(23) where
$u_{\mu} = -\dfrac{\rm i}{2} \left[u^{\dagger}(\partial_{\mu}u) -u (\partial_{\mu}u^\dagger) \right] \;\;{\rm{and}}\;\; u = \text{exp}\left[ \dfrac{\rm i}{\sqrt{2}\sigma_{0}}P\gamma_{5}\right]$

In the present investigation, we have taken the interactions up to the second order. X and P represent the scalar and pseudoscalar meson matrices [35], respectively, and are explicitly given as
$ X = \frac{1}{\sqrt{2}}\sigma^a \lambda_a = \left( \begin{array}{ccc} (\delta +\sigma)/\sqrt{2} & \delta^+ & \kappa^+\\ \delta^- & (-\delta+\sigma)/\sqrt{2} & \kappa^0 \\ \kappa^- & \overline{\kappa^0}& \zeta \end{array} \right), $

(24) and
$ P = \frac{1}{\sqrt{2}}\pi_a \lambda^a = \left (\begin{array}{ccc} \dfrac{1}{\sqrt{2}}\left ( \pi^0+{\dfrac {\eta}{\sqrt {1+2\,{w}^{2}}}}\right )&\pi^+ &2\,{\dfrac {K^+}{w+1}}\\ \pi^-&\dfrac{1}{\sqrt{2}}\left (- \pi^0+ {\dfrac {\eta}{\sqrt {1+2\,{w}^{2}}}}\right )&2\,{\dfrac { K^0 }{w+1}}\\ 2\,{\dfrac {K^-}{w+1}}&2\,{\dfrac { \overline{K}^0}{w+1}}&-{\dfrac {\eta\,\sqrt {2}}{\sqrt {1+2\,{w}^{2}}}} \end{array}\right ). $ 
(25) In Eq. (23), the axial current calculations for pions and kaons result in the following relations:
$ \sigma_0 = -f_{\pi} \qquad \zeta_0 = -\frac{1}{\sqrt{2}}(2 f_K - f_{\pi}) , $

(26) for the vacuum values of the scalar condensates σ and ζ found in the linear σ-model [9]. In Eq. (25), the re-normalization factor
$ w = \sqrt{2}\zeta_0/\sigma_0 $ is incorporated to obtain the canonical form of the kinetic energy terms [9]. The matrix P reduces to the matrix normally used in chiral perturbation theory [35] for$ w = 1 $ (i.e.,$ f_{\pi} $ =$ f_K $ ). The advantage of$ w\neq 1 $ is that the SU(3)V breaking effects are accounted for in the P matrix for even the lowest orders [35].$2.$ ${\cal{L}}_{\eta\rm SB}$ , the mass term:The second term in Eq. (22), represents the scale breaking term of the chiral model Lagrangian, which is given by
$ {\cal{L}}_{\rm SB} = -\frac{1}{2} {{\rm{Tr}}} A_p \left(uXu+u^{\dagger}Xu^{\dagger}\right), $

(27) with
$ A_p $ as a diagonal matrix, given as$ A_p = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} m_{\pi}^2 f_{\pi}& 0& 0\\ 0 & m_\pi^2 f_\pi& 0\\ 0 & 0& 2 m_K^2 f_K -m_{\pi}^2 f_\pi \end{array} \right). $

(28) The η meson vacuum mass is extracted from the Lagrangian [Eq. (27)] and given as
$ m_{\eta} = \frac{1}{f}\sqrt{-\frac{1}{2}\Big(8 f_K f_\pi (m_\pi^2+m_K^2)-16 f_K^2 m_K^2-6f_\pi^2 m_\pi^2 \Big)}. $

(29) Using the values of various constants, the value of
$ m_{\eta} $ is found to be 574.374 MeV, which has an accuracy of 4.9 % compared to the experimental mass, i.e., 547.862 MeV [86]. Moreover, using the Gell-Mann Okubo mass formula under octet approximation, the vacuum mass of η-mesons is calculated as 567 MeV, which has an accuracy of 3.6% compared to the physical mass [87]. Model dependencies have been observed in the vacuum mass of η-mesons [87]; however, in the current scenario, the in-medium mass-shift of η-mesons is nearly the same for both obtained masses and therefore can be neglected.$3.$ ${\cal{L }}_{d_1}^{\rm BM}+ {\cal{L }}_{d_2}^{\rm BM}$ , the d terms:The final two terms in the Eq. (22) arise from the baryon-meson interaction Lagrangian terms of the chiral model [33, 88] and are given as
$ {\cal{L }}_{d_1}^{\rm BM} = \frac {d_1}{2} {\rm Tr} (u_\mu u ^\mu){\rm Tr}( \bar B B), $

(30) and
$ {\cal{L }}_{d_2}^{\rm BM} = d_2 {\rm Tr} (\bar B u_\mu u ^\mu B). $

(31) In the above, B denotes the baryon matrix, given as
$ B = \frac{1}{\sqrt{2}}b^a \lambda_a = \left( \begin{array}{ccc} \dfrac{\Sigma^0}{\sqrt{2}} +\dfrac{\Lambda^0}{\sqrt{6}}& \Sigma^+ & p\\ \Sigma^- & -\dfrac{\Sigma^0}{\sqrt{2}} +\dfrac{\Lambda^0}{\sqrt{6}} & n \\ \Xi^- & \Xi^0& -2 \dfrac{\Lambda^0}{\sqrt{6}} \end{array} \right). $

(32) Explicit forms of the above three terms are inserted into Eq. (22), and the interaction Lagrangian is given as
$ \begin{aligned}[b] \mathcal{L_{\eta }} = \left( \frac{1}{2}-\frac{\sqrt{2}\sigma ^\prime f_\pi + 4 \zeta ^\prime (2 f_K-f_\pi) }{\sqrt{2}f^2} \right) \partial^{\mu}\eta\partial_{\mu}\eta \end{aligned} $

$ \begin{aligned}[b] \quad\quad&-\frac{1}{2}\left( m_{\eta}^2 -\frac{(\sqrt{2}\sigma ^\prime -4 \zeta ^\prime )m^2_\pi f_\pi + 8 \zeta ^\prime m^2_K f_K}{\sqrt{2} f^2} \right) \eta^2\\ &+\frac{d'}{f^2} \left( \frac{\rho^s_p+\rho^s_n}{4} \right) \partial^{\mu}\eta\partial_{\mu}\eta. \end{aligned} $

(33) In the above, the fields
$ \sigma'( = \sigma-\sigma _0) $ ,$ \zeta'( = \zeta-\zeta_0) $ , and$ \delta'( = \delta-\delta_0) $ are the digressions of the scalar field expectation values from their vacuum expectation values, the constant f is equal to$ \sqrt{f_\pi^2+2(2 f_K - f_\pi)^2} $ , and the parameter$ d' $ =$ 3d_1+d_2 $ .At the mean-field level, the equation of motion for the η meson field is simplified to
$ \begin{aligned}[b] & \partial^{\mu}\partial_{\mu} \eta +\left( m_{\eta}^2-\frac{(\sqrt{2}\sigma ^\prime -4 \zeta ^\prime )m^2_\pi f_\pi + 8 \zeta ^\prime m^2_K f_K}{\sqrt{2} f^2} \right)\eta \\ &+\frac{2}{f^2} \left( \frac{(\rho^s_p+\rho^s_n)d'}{4} -\frac{\sqrt{2}\sigma ^\prime f_\pi + 4 \zeta ^\prime (2 f_K-f_\pi) }{\sqrt{2}} \right) \partial^{\mu} \partial_{\mu} \eta = 0. \end{aligned} $

(34) Furthermore, the dispersion relation for the η meson field is obtained by Fourier transformation of the above equation
$ -\omega^2+ {\vec k}^2 + m_\eta^2 -\Pi^*(\omega, |\vec k|) = 0, $

(35) where
$ \Pi^* $ symbolizes the in-medium self-energy of η mesons and is explicitly given as$ \begin{aligned}[b] \Pi^* (\omega, |\vec k|)= & \frac{(\sqrt{2}\sigma ^\prime -4 \zeta ^\prime )m^2_\pi f_\pi + 8 \zeta ^\prime m^2_K f_K}{\sqrt{2} f^2} \\& +\frac{2d'}{f^2} \left( \frac{\rho^s_p+\rho^s_n}{4} \right) (\omega ^2 - {\vec k}^2) \\ &- \frac{2}{f^2} \left( \frac{\sqrt{2}\sigma ^\prime f_\pi + 4 \zeta ^\prime (2 f_K-f_\pi) }{\sqrt{2}} \right) (\omega ^2 - {\vec k}^2). \end{aligned} $

(36) In asymmetric nuclear matter, the in-medium mass of η mesons is evaluated by solving Eq. (35) under the condition
$ m_{\eta}^* = \omega(|\vec k| $ = 0). The parameter$ d' $ in the expression of self energies is estimated from the empirical value of the scattering length$ a^{\eta N} $ of η mesons [35], whose expression is given as$ \begin{aligned}[b] d' =& 8 \pi \left (1+\frac{m_\eta}{M_N}\right ) f^2 \frac{ a^{\eta N}}{m^2_\eta} +\frac{\sqrt{2}g_{\sigma N}f_\pi}{m^2_\sigma}-\frac{4 \sqrt{2} (2f_K-f_\pi) g_{\zeta N}}{m^2_\zeta} \\ &- \left( \frac{\sqrt{2} g_{\sigma N}}{m^2_\sigma}-\frac{4 g_{\zeta N}}{m^2_\zeta} \right )\frac {m^2_\pi f_\pi} {\sqrt{2} m^2_\eta}- \frac{4\sqrt{2} g_{\delta N}m^2_K f_K}{m^2_\delta m^2_\eta}, \end{aligned} $

(37) where
$ m_{\sigma} $ ,$ m_{\zeta} $ ,$ m_{\delta} $ , and$ m_{N} $ denote the vacuum masses of the fields σ, ζ, δ, and nucleons, respectively, and their values are given in Table 1. The use of these parameters in the above equation gives$ d' $ = 0.0435. Furthermore, using the in-medium mass of η mesons, the optical potential for η-mesons at finite momentum [10, 89] in nuclear matter is given by$ U^*_{\eta}(\omega, \vec{k}) = \omega (\vec{k}) -\sqrt {\vec{k}^2 + m^2_{\eta}}, $

(38) and for zero momentum, the relation becomes
$ U^*_{\eta} = \Delta m_\eta^* = {m_{\eta}^*}-m_{\eta}. $

(39) -
ChPT is a phenomenological approach for studying the low-energy dynamics of QCD with an effective field theory Lagrangian based on the underlying chiral symmetry of quantum chromodynamics [35]. Here, the SU(3)
$ _{\mathrm{L}}\times $ SU(3)R Lagrangian describing the pseudoscalar meson and baryon interactions is given as$ {\mathcal{L}_{\text{ChPT}} } = {\mathcal{L}_{\rm P} }+{\mathcal{L}_{\rm P B} }, $

(40) where the pseudoscalar mesonic term,
$\mathcal{L}_{\rm P}$ , is taken up to the second chiral order [35, 64] and is given by [35]$ {\mathcal{L}_{\rm P} } = \frac{1}{4}f_\pi^{2}\, {\rm Tr}\, \partial^{\mu}\Sigma\partial_{\mu}\Sigma^{\dagger} +\frac{1}{2}f_\pi^2 B_0 \left\{\rm{Tr} M_{q}(\Sigma-1)+\mathrm{H.c.}\right\}. $

(41) In the above equation,
$ \Sigma = \xi^2 = \exp{(i\sqrt{2}P/f_\pi)} $ , the symbol$ B_0 $ represent the connection with the order parameter of spontaneously broken chiral symmetry, and$M_{q} = $ $ \rm{diag}\{m_{q}, m_{q}, m_{s}\}$ is the current quark mass matrix. The second term in Eq. (40),$\mathcal{L}_{\rm P B}$ , defines the leading order and next-to leading order baryon-meson interactions [64]. The off-shell terms are developed using heavy baryon chiral theory [34]. However, the former theory has additional properties, such as quantum corrections and Lorentz invariance. The properties of the nuclear system have been described successfully using the off-shell Lagrangian, and the higher-order terms of this next-to-leading order Lagrangian have also been studied [90]. In the present study, we limited our calculations up to the small momentum scale,$ Q^{2} $ , without loop contributions (for s-wave$ \eta {N} $ scattering) because the higher order corrections are suppressed [35].Using heavy-baryon approximation, and expanding Eq. (40) up to the order of
$ 1/f_\pi^2 $ , we obtain the$ \eta N $ Lagrangian as$ \begin{aligned}[b] \mathcal{L_{\eta N }} = & \frac{1}{2}\partial^{\mu}\eta\partial_{\mu}\eta -\frac{1}{2}\left( m{^\prime}_{\eta}^2 -\frac{\Sigma_{\eta {N}}}{f_\pi^2}\bar{\Psi}_{{N}}\Psi_{{N}} \right) \eta^2\\&+\frac{1}{2}\frac{\kappa}{f_\pi^2}\bar{\Psi}_{{N}}\Psi_{{N}}\partial^{\mu}\eta\partial_{\mu}\eta. \end{aligned} $

(42) In the above equation,
$ m_{\eta} $ represent the mass of η-mesons calculated in ChPT and is evaluated through the relation$m{^\prime_{\eta}}^2 = $ $ \dfrac{2}{3}B_0 (m_q+2m_s)$ . In this mass relation,$ m_{q(s)} $ defines the mass of light (strange) quarks [87]. We used the same η meson vacuum mass value, i.e.,$ m{^\prime}_{\eta} $ =$ m_{\eta} $ = 574.374 MeV, in the ChPT+chiral model calculations for consistency with the chiral SU(3) model. Moreover,$ \Sigma_{\eta\mathrm{N}} $ , the$ \eta N $ sigma term, and the κ term are determined by the relations$ \Sigma_{\eta {N}} = -\frac{2}{3}[a_{1}m_{q}+4a_{2}m_{s}+2a_{3}(m_{q}+2m_{s})], $

(43) and
$ \kappa = 4\pi f_\pi^2 \left( \frac{1}{m_{\eta}^2}+\frac{1}{m{^\prime}_{\eta}M_{ {N}}} \right) a^{\eta {N}} -\frac{\Sigma_{\eta {N}}}{m_{\eta}^2}, $

(44) respectively. The a terms in Eq. (43) correspond to chiral breaking effects and are fitted from the parameter
$\Sigma_{ {KN}} = 380\pm 100$ MeV, where$ \pm 100 $ MeV reflects the uncertainty [35, 65, 66, 91-95]. The parameter κ is estimated from the ηN scattering length [35] with a range of$a^{\eta {N}}$ values, i.e., 0.91 ~ 1.14 fm, which is assumed from empirical investigations [35, 96-99].The equations of motion for
$ \eta N $ interactions in the unified approach of the chiral SU(3) model and ChPT can be written as$ \left( \partial_{\mu}\partial^{\mu} +m_{\eta}^2 -\frac{\Sigma_{\eta N}}{2f_\pi^2}\langle \bar{\Psi}_{ {N}}\Psi_{ N} \rangle +\frac{\kappa}{2f_\pi^2}\langle \bar{\Psi}_{N}\Psi_{N} \rangle\partial_{\mu}\partial^{\mu} \right) \eta = 0, $

(45) where
$\langle \bar{\Psi}_{ {N}}\Psi_{ {N}}\rangle \equiv \rho^s_{N}$ =$ \left(\rho^s_{p}+\rho^s_{n} \right) $ is the magnetic field influenced scalar density of a nucleon calculated within the chiral SU(3) model. The plane wave decomposition of Eq. (45) gives$ -\omega^2+\vec {{k}}^2+m_{\eta}^2 -\frac{\Sigma_{\eta {N}}}{2f_\pi^2}\rho^s_{N} +\frac{\kappa}{2f_\pi^2}\rho^s_{N} \left(-\omega^2+\vec{{k}}^2\right) = 0. $

(46) By solving the above quadratic equation, we obtain
$ \omega = \sqrt{{m_{\eta}^*}^2 +\vec{{k}}^2}, $

(47) and the explicit expression for the magnetic field induced mass of η mesons,
$ m_{\eta}^* $ , is given by$ m_{\eta}^* = \sqrt{ \left(m_{\eta}^2-\frac{\Sigma_{\eta {N}}}{2f_\pi^2}\rho^s_{N}\right) \Bigg/ \left(1+\frac{\kappa}{2f_\pi^2}\rho^s_{N}\right) }. $

(48) The final two terms of Eq. (46) provides the η-meson self-energy
$ \Pi^*(\omega,\vec{{k}}) = \Bigg (-\frac{\Sigma_{\eta {N}}}{2f_\pi^2} +\frac{\kappa}{2f_\pi^2} (-\omega^2+\vec{{k}}^2)\Bigg ) \rho^s_{N}, $

(49) where ω is the η-meson single-particle energy and
$ \vec{{k}} $ is the momentum. -
In this section, we discuss the magnetic field induced optical potential of η mesons evaluated using two approaches: (i) the chiral SU(3) model in Section III.A and (ii) ChPT + chiral SU(3) model in Section III.B. In both methodologies, we have taken the values of scattering length,
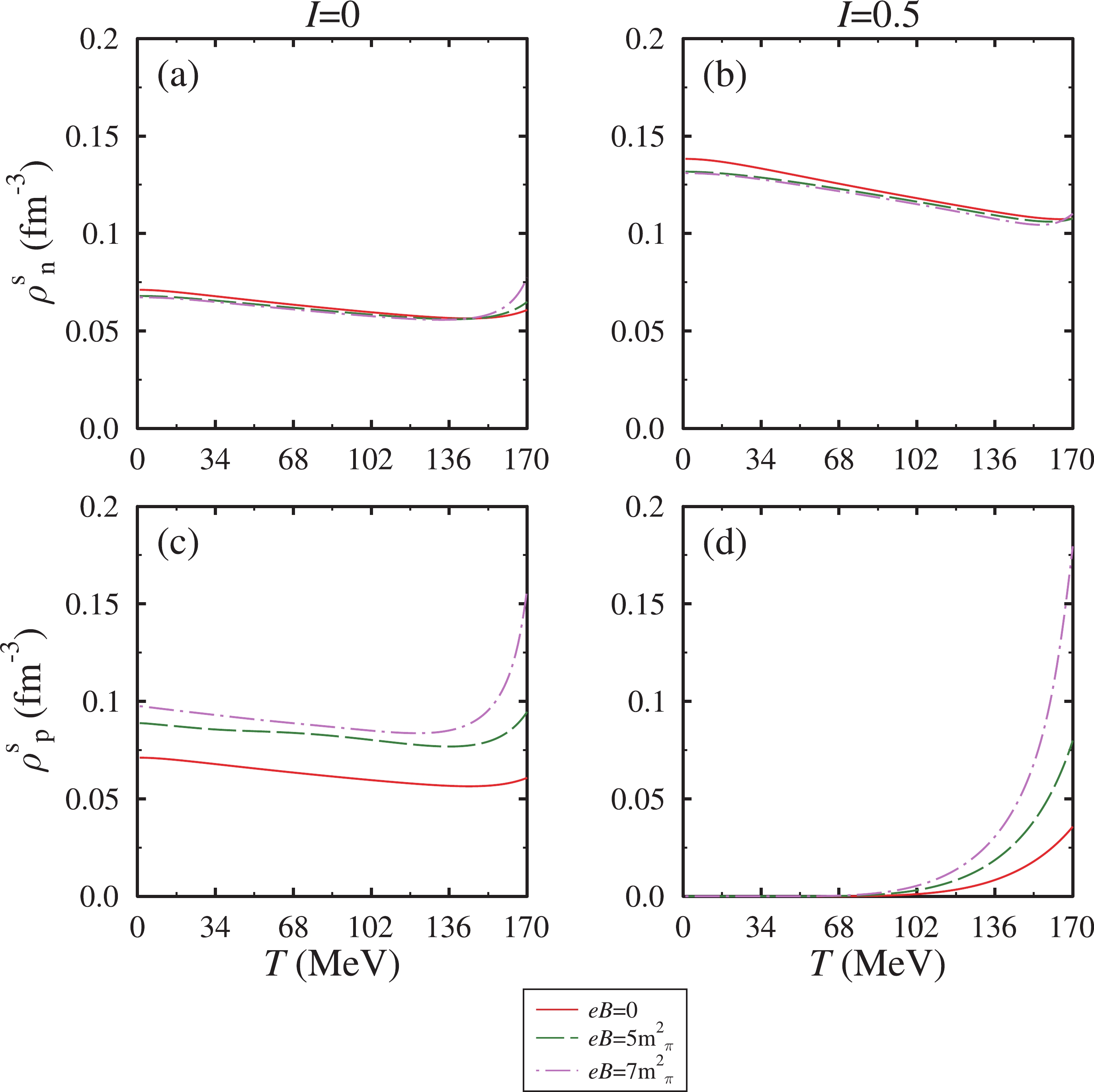
$a^{\eta N}$ , in the range 0.91-1.14 fm. We begin by discussing the in-medium behavior of nucleon scalar densities under the influence of a strong magnetic field for different values of nuclear density, isospin asymmetry, and temperature.In Fig. 1, at the nuclear saturation density, we illustrate the scalar densities of neutrons and protons as a function of temperature for zero and non-zero values of the magnetic field. In the left (right) column of the figure, we present the scalar densities for symmetric (anti-symmetric) nuclear matter. For symmetric nuclear matter and a zero magnetic field, we observe the same neutron and proton scalar density behavior according to temperature. The scalar densities slowly decrease linearly up to
$ T \approx $ 150 MeV and begin increasing for higher values of temperature. These modifications reflect the interplay between contributions from higher momenta states and the thermal distribution functions in the scalar density expressions [see Eqs. (16) and (14)]. Further, upon increasing the magnetic field, the proton and neutron scalar densities behave unevenly; for a particular temperature value, the proton scalar density increases significantly, whereas the neutron scalar density slightly decreases. The additional effects on the proton scalar density are caused by the charged nature of protons, the positively charged proton interacts with the magnetic field and experiences Landau quantization, and contributions from the anomalous magnetic moment [see Eq. (16)]. In contrast, owing to its uncharged nature, the neutron only experiences contributions from the anomalous magnetic moment [see Eq. (14)]. Moreover, the transition temperature decreases with an increase in the magnetic field, which supports the restoration of chiral symmetry [72]. For asymmetric nuclear matter [sub-plot (b) and (d)], unequal values of proton and nucleon scalar densities are obtained, even with zero magnetic field. In the chiral SU(3) model, the scalar densities of protons and neutrons are calculated through Eq. (16) and Eq. (14), respectively; these equations include the effects of in-medium scalar and vector fields [9]. In asymmetric nuclear matter, the iso-scalar(vector)$ \delta(\rho) $ field presents non-zero contributions, which eventually leads to unequal values of proton and neutron densities [36]. The neutron scalar density modifies significantly in the asymmetric nuclear medium and decreases with an increase in the temperature, whereas the proton scalar density exhibits a zero value up to$ T \approx $ 90 MeV and then increases rapidly. The proton scalar density value is expected to be zero for I = 0.5; however, despite$ \rho^v_p $ = 0, the proton condensate ($ \bar p p $ ) still populates nuclear matter at high temperatures. The inclusion of the magnetic field significantly changes the proton scalar density, whereas the neutron scalar density shows a small decrement with increasing magnetic field.In Fig. 2, we plot scalar densities for the same medium parameter values except for
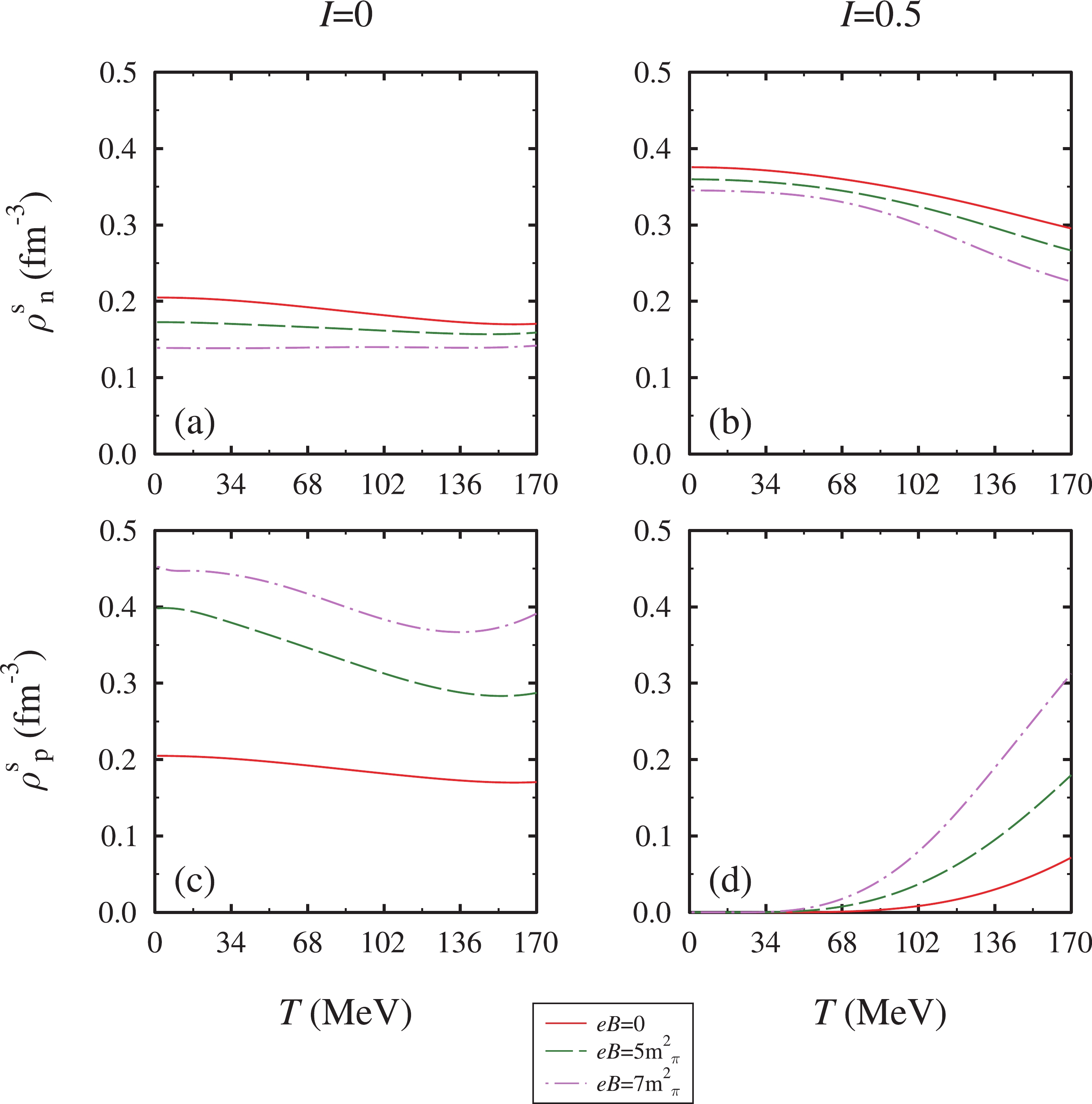
$ \rho_N $ = 4$ \rho_0 $ . On the same line, at$ eB $ = 0 and I = 0, we observe a similar behavior of the proton and neutron scalar densities. When moving from zero to non-zero values of magnetic field strength, for a particular value of temperature, the proton scalar density increases appreciably, whereas the neutron scalar density slightly decreases. This is again caused by the additional energy levels in protons owing to magnetic field intervention. It is noted that the effect of the magnetic field is more pronounced in the high density regime. Furthermore, at the highest value of medium asymmetry, as a function of temperature, the proton scalar density remains zero up to$ T \approx $ 50 MeV and further increases non-linearly with an increase in the magnetic field. Conversely, the neutron scalar density modifies appreciably in asymmetric matter; it decreases with an increase in temperature and magnetic field. In symmetric nuclear matter, the observed scalar densities at zero magnetic field are in agreement with the results of the relativistic mean-field model [35, 61]. -
In this section, we present the results and discussion for the in-medium mass of η-mesons calculated in the chiral SU(3) model under the influence of the external magnetic field. In Figs. 3 and 4, we illustrate the in-medium η mass as a function of temperature with different values for the additional parameters, such as isospin asymmetry, the magnetic field, and scattering length at
$ \rho_N $ =$ \rho_0 $ and 4$ \rho_0 $ , respectively. In Fig. 3, for any value of I,$ eB $ , and$ a^{\eta N} $ , the in-medium mass gradually increases with an increase in temperature up to a certain temperature value and then begins decreasing. This behavior represents an opposite reflection of the in-medium scalar densities plotted in Fig. 1 because the expression for η-mesons [see Eq. (48)] has an inverse dependence on the sum of nucleon scalar densities. In symmetric nuclear matter, the impact of the magnetic field results in a more attractive contribution in the in-medium η mass for a particular value of temperature and scattering length. With an increase in the magnetic field, the transition point (i.e., the temperature at which the in-medium mass begins decreasing as a function of temperature) moves toward the lower temperature side. As discussed earlier, the medium modified mass of η-mesons has an indirect dependence on the sum of the nucleon's scalar densities; therefore, it exhibits an opposite behavior to the scalar densities. However, in asymmetric nuclear matter, the in-medium mass slowly increases for zero magnetic field, as was observed for symmetric matter. This is because the in-medium mass depends on the sum of the scalar densities with no additional parameter dependence. Furthermore, at$ I \neq $ 0, we observe a small change in the η mass at the lower temperature region, whereas a substantial change is observed in the higher temperature region in terms of the magnetic field. This is because, in highly asymmetric matter at lower (higher) temperatures, there is a negligible (substantial) contribution to the proton scalar density. We note that, owing to the uncharged nature of η-mesons, they does not directly couple with the magnetic field and therefore do not present any additional contributions from the Landau energy levels, as was observed for charged D mesons [6, 19, 72]. From Fig. 3, we also anticipate the effect of the scattering length. When$ a^{\eta N} $ is altered from 0.91 to 1.14 fm, we observe a significant decrement in the effective mass for a particular value of the magnetic field and temperature. This is due to the direct relationship between the parameter$ d^\prime $ and the scattering length in Eq. (37). The$ d^\prime $ parameter provides an attractive contribution to the η in-medium mass through the equations of motion [Eq. (35)] and self-energy [Eq. (36)].In Fig. 4, we plot the in-medium mass of η-mesons with the same medium parameter values except for
$ \rho_N $ = 4$ \rho_0 $ . In the left panel, at$ eB $ = 0 and I = 0, we observe a similar trend for the in-medium mass as a function of temperature, as was observed for ρ =$ \rho_0 $ . At a high nuclear density, we observe a significant reduction in the mass of the η-mesons. The reduction in the effective mass increases with an increase in the magnetic field and scattering length. When we move from symmetric nuclear matter to asymmetric nuclear matter, we observe the cross-over behavior of the in-medium mass as a function of temperature for a particular scattering length value. This is due to a similar reason as was discussed for the nuclear saturation density case. However, in the high density regime, the proton scalar density populates little (but greater than the ρ =$ \rho_0 $ case) in the lower temperature regime and substantially in the higher temperature regime. Moreover, the effect of the magnetic field is more pronounced in the high density regime.Furthermore, for a better understanding of the in-medium η-meson mass, in Fig. 5, we plot the individual terms of η-meson self-energy. The expression for self-energy [Eq. (36)] has three interaction terms: (i) the first range term (ii) mass term, and (iii)
$ d^\prime $ term. In this figure, we present the contributions of the individual terms as a function of temperature and asymmetry for$ a^{\eta N} $ = 1.02 fm at the nuclear saturation density. At zero magnetic field and asymmetry, we anticipate that the first range term provides a significant repulsive contribution to the in-medium mass, whereas the mass and$ d^\prime $ terms provide small and significant attractive contributions, respectively. At a non-zero magnetic field (asymmetry), the modification in the$ d^\prime $ term increases (decreases). This behavior is due to the presence of the nucleon scalar density terms in the second term of the self-energy expression [Eq. (36)]. The$ d^\prime $ term dependence emphasizes the importance of the scattering length,$ a^{\eta N} $ , in eta-nucleon interactions.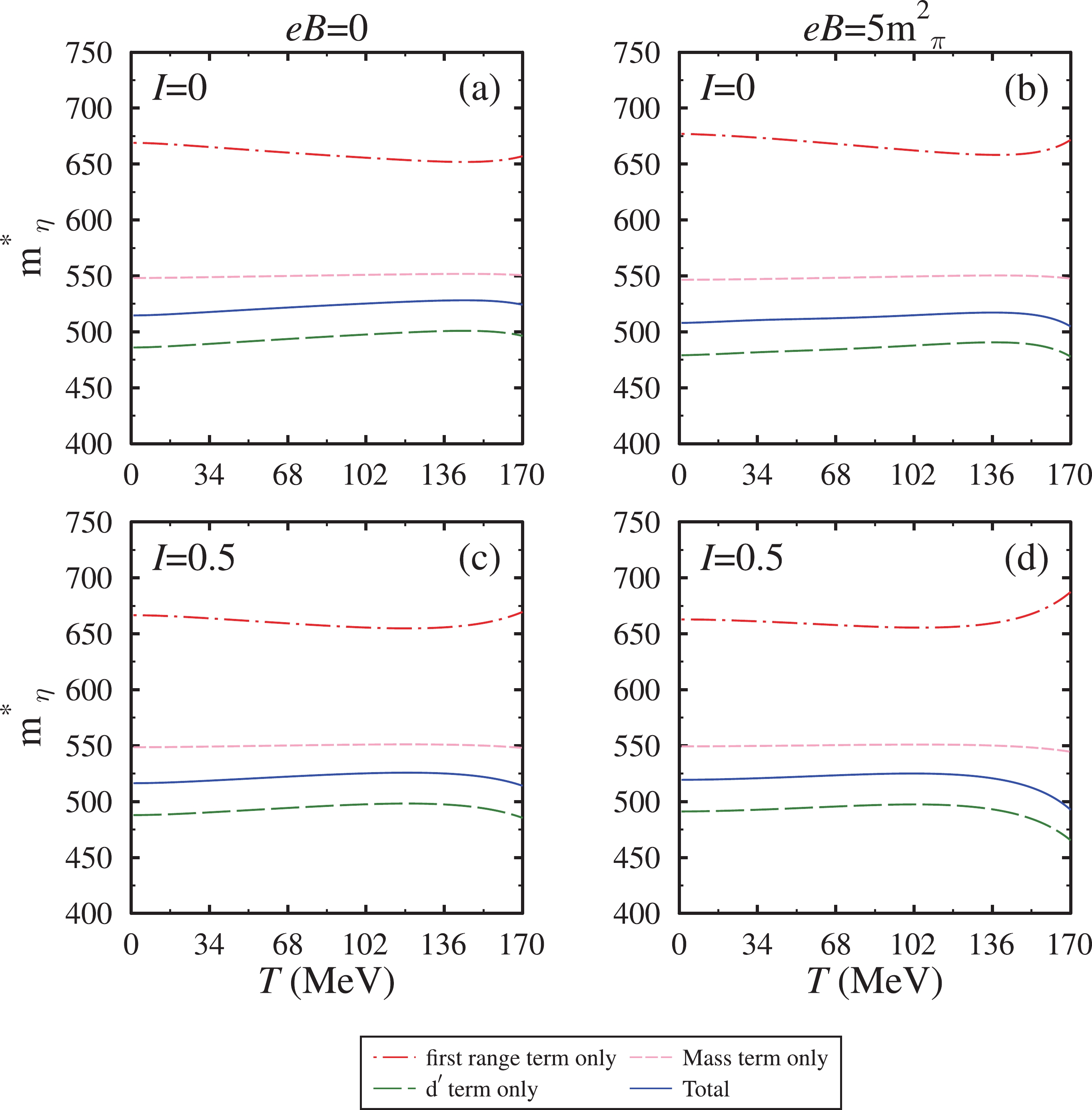
Figure 5. (color online) The different terms of in-medium η meson mass in the chiral model at
$\rho_0$ and$a^{\eta N}$ =1.02 fm.The optical potential at zero and non zero momentum can be used to study η-mesic nuclei [34-36] and eta-meson momentum dependence [55, 62, 63]. In Fig. 6, for symmetric nuclear matter, we plot the optical potential as a function of medium momentum
$ \lvert \vec{k}\rvert $ for various values of the magnetic field and density at$ a^{\eta N} $ = 0.91 fm. In this figure, at$ \rho_N $ =$ \rho_0 $ , the magnitude of the optical potential decreases with an increase in momentum. With an increase in the magnetic field (temperature), the reduction in the optical potential increases (decreases). The behavior of the in-medium optical potential reflects the interplay between the in-medium mass and momentum, which can be understood from the expression given by Eq. (38). At higher momentum$ \lvert \vec{k} \rvert $ values, in the optical potential curve, the contribution of the effective mass is suppressed by the increase in the momentum states. Furthermore, in the right panel, i.e., the high density regime, we anticipate a deep optical potential that becomes less as the momentum states increase. In Figs. 7 and 8, we discover a similar trend in the optical potential with η momentum. In these figures, we observe a deeper optical potential with increasing scattering length. The behavior of the optical potential with scattering length and other medium parameters can be understood in terms of the in-medium mass. For a clearer illustration, the values of the in-medium optical potential in the chiral SU(3) model at$ \lvert \vec{k} \rvert $ = 0 are listed in Table 2.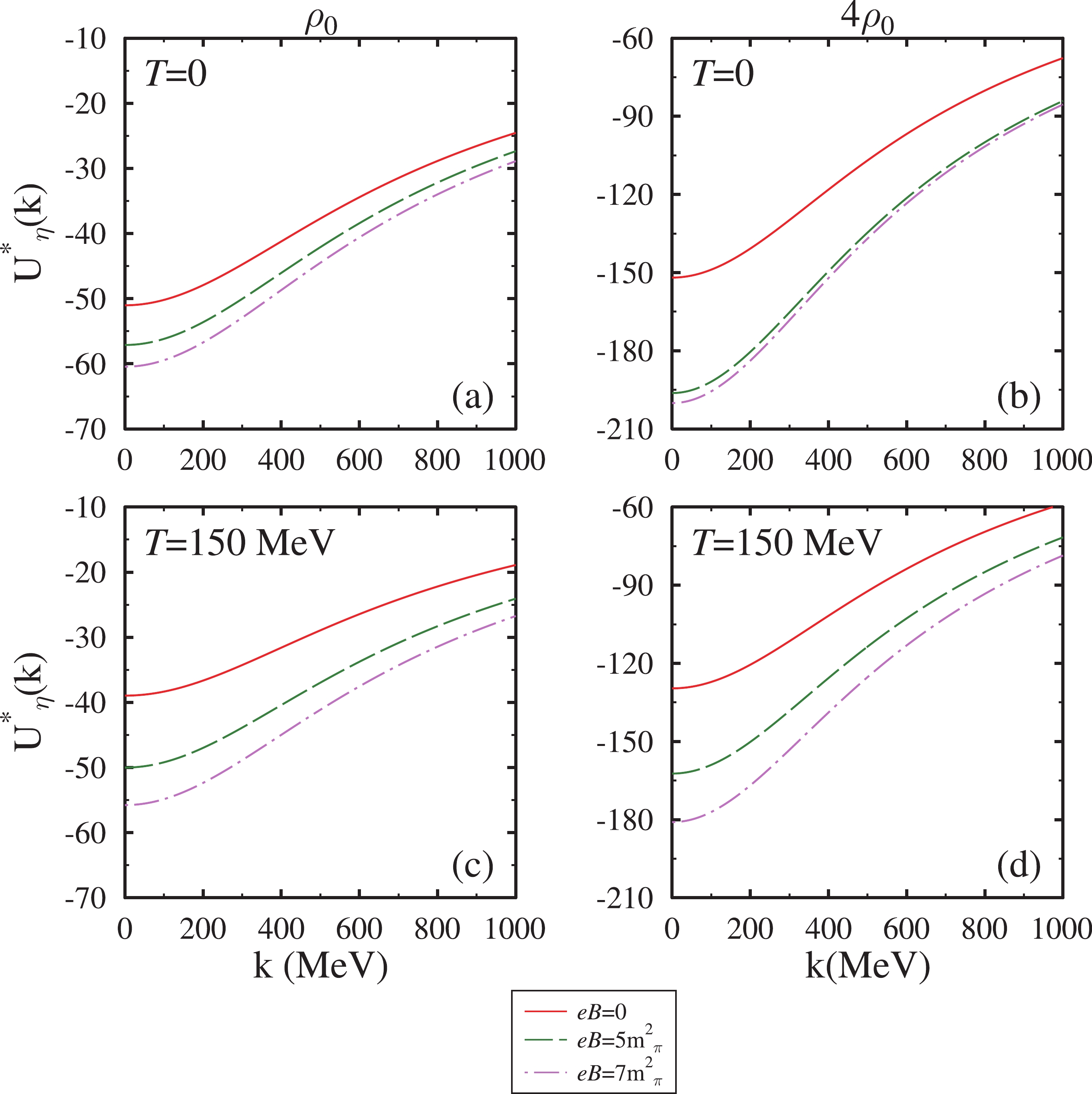
Figure 6. (color online) The in-medium η meson optical potential in the chiral model at
$a^{\eta N}$ =0.91 fm and I=0.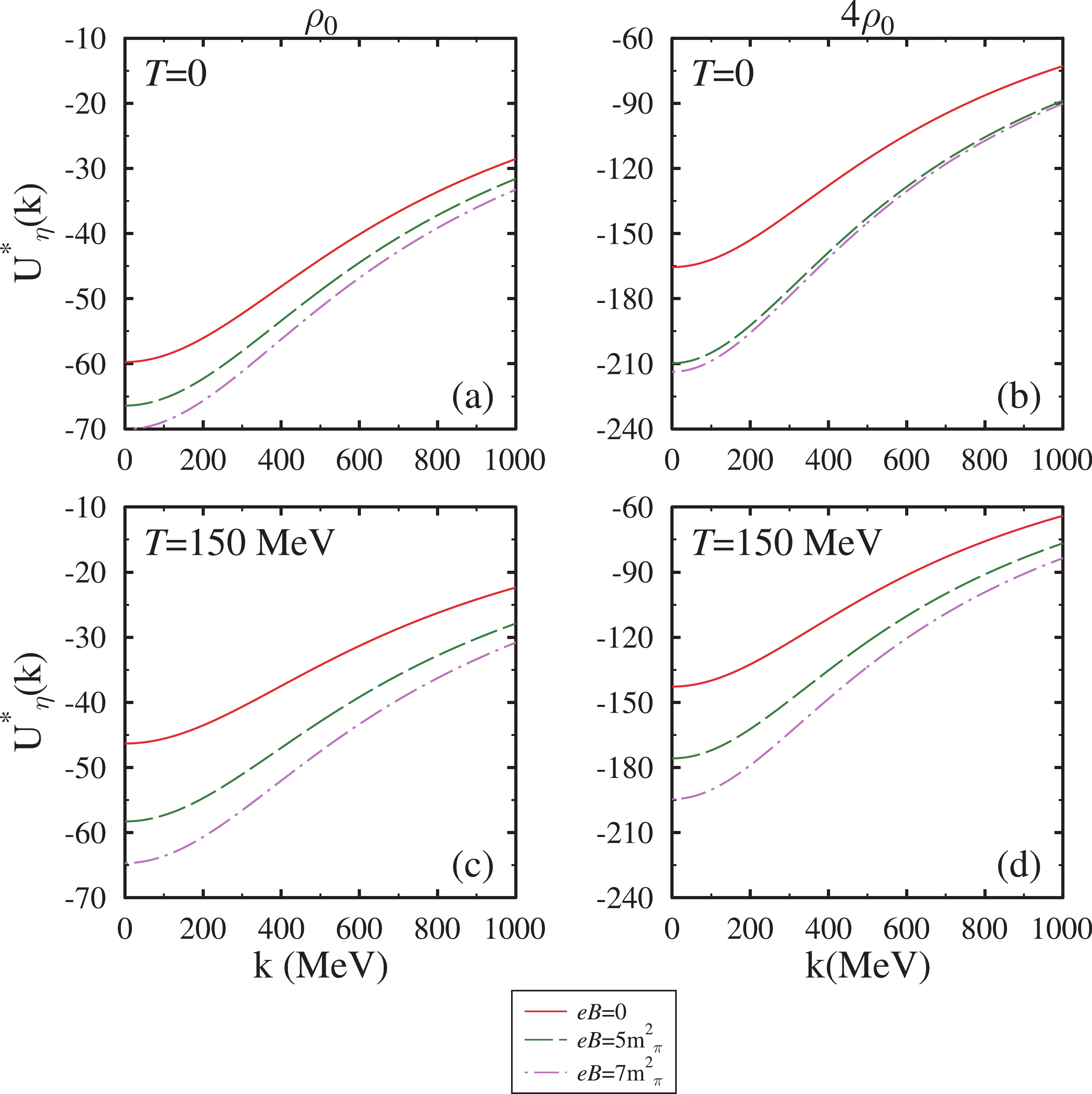
Figure 7. (color online) The in-medium η meson optical potential in the chiral model at
$a^{\eta N}$ =1.02 fm and I=0.
Figure 8. (color online) The in-medium η meson optical potential in the chiral model at
$a^{\eta N}$ =1.14 fm and I=0.I=0 I=0.5 $a^{\eta N}/\text{fm}$ 

T=0 MeV T=100 MeV T=0 MeV T=100 MeV $eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$ \Delta m^*_\eta$ 

0.91 −51.02 −57.11 −41.63 −51.26 −49.43 −46.69 −41.61 −41.66 1.02 −59.73 −66.42 −49.31 −59.74 −57.97 −54.93 −49.28 −49.32 1.14 −68.75 −76.02 −57.31 −68.52 −66.83 −63.50 −57.28 −57.32 Table 2. In-medium mass-shift (MeV) of the η-mesons with and without considering the effect of the magnetic field at
$\rho=\rho_0$ and different parameters calculated in the chiral SU(3) model. -
In this section, we evaluate the in-medium masses of η-mesons using the joint chiral SU(3) model and chiral perturbation theory approach and compare the results with those calculated using the chiral SU(3) model alone. As discussed in Section II.A.2, the
$ \eta N $ equation of motion is derived from the ChPT$ \eta N $ Lagrangian density. The magnetic field influenced scalar density of nucleons in ChPT self-energy [Eq. (49)] is taken from the chiral SU(3) model discussed in Section II.A. In the present study, we set the value of parameter$ \Sigma_{\eta N} $ as 280 MeV by neglecting the uncertainties in the parameter [36]. We will see later that the contribution of the$ \Sigma_{\eta N} $ term is less than that of the kappa term.In Figs. 9 and 10, we plot the mass ratio
$ m^*_\eta/m_\eta $ with respect to temperature, scattering length, and isospin asymmetry at$ \rho_N $ =$ \rho_0 $ and 4$ \rho_0 $ , respectively. In these figures, we have also compared the in-medium masses obtained from different approaches, i.e., (i) ChPT and the chiral model and (ii) the chiral model alone. In Fig. 9, using the joint approach, we observe a significant decrement in the in-medium mass of η-mesons at the nuclear saturation density. We find a similar behavior of the medium modified η-meson mass in terms of the magnetic field, isospin asymmetry, and scattering length, as was found in observations of the chiral SU(3) model. The substantial decrement in the joint approach is a consequence of the lack of a repulsive contribution term in ChPT. The net contribution in ChPT originates from the$ \Sigma_{\eta N} $ and κ terms (both attractive in nature). In Fig. 10, at a higher value of nuclear density, the trend of the mass ratio with temperature remains the same; however, a more negative mass-shift is observed. The ratio reveals a similar behavior regarding other medium parameters and the scattering length. To obtain a clear understanding, in Fig. 11, at$ \rho_N $ =$ \rho_0 $ and$ a^{\eta N} $ = 1.02 fm, we illustrated the in-medium behavior of the individual terms present in the ChPT self-energy of magnetized asymmetric nuclear matter that contributed to the in-medium mass of η-mesons through Eq. (48). From this figure, we observe that the contribution of the$ \Sigma_{\eta N} $ term is negative but much less than that of the κ term. The κ term has a significant attractive contribution to the in-medium mass because the numerator of the in-medium mass mathematical relation, given by Eq. (48), has a negative contribution of nucleon scalar density, whereas the denominator has a positive contribution. Therefore, due to this inverse relationship, the value of the effective mass decreases with an increase in scalar density. The values of the in-medium optical potential at zero momentum calculated using ChPT+chiral model are given in Table 3.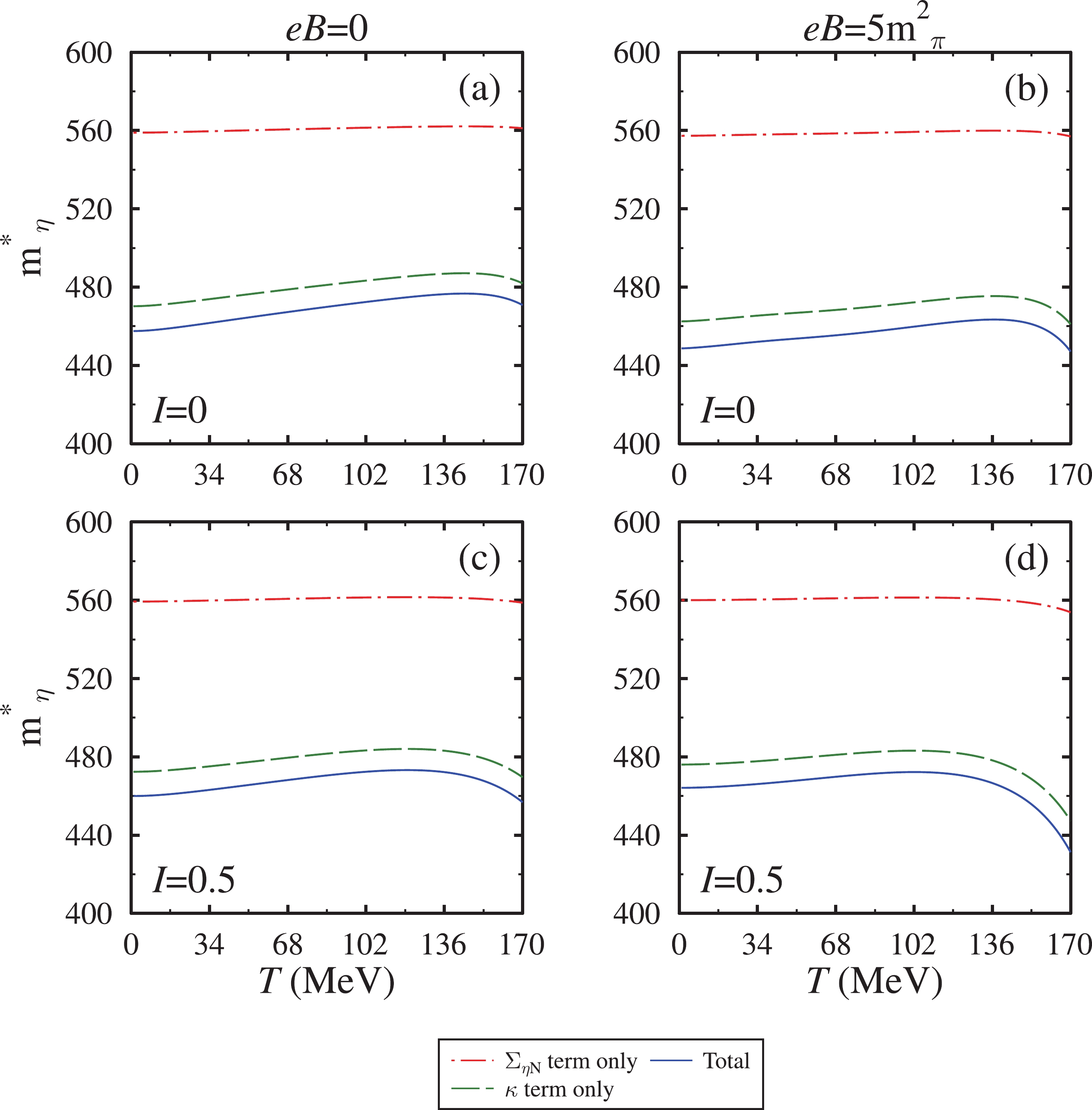
Figure 11. (color online) The different terms of the in-medium η meson mass in ChPT+the chiral model at
$\rho_0$ and$a^{\eta N}$ =1.02 fm.$a^{\eta N} /\text{fm}$ 

I=0 I=0.5 T=0 MeV T=100 MeV T=0 MeV T=100 MeV $eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$eB$ =0

$eB$ =5

${{m^2_{\pi}}}$ 

$ \Delta m^*_\eta$ 

0.91 −107.57 −115.95 −93.79 −105.70 −105.25 −102.11 −93.72 −93.70 1.02 −116.83 −125.69 −102.21 −114.89 −114.35 −110.22 −102.11 −102.17 1.14 −126.36 −135.64 −110.96 −124.32 −123.75 −119.42 −110.86 −110.93 Table 3. In-medium mass-shift (MeV) of η-mesons with and without considering the effect of the magnetic field at
$\rho=\rho_0$ and different parameters calculated in the ChPT+the chiral SU(3) model.To the best of our knowledge, no work has been performed to study the effect of a magnetic field on the in-medium mass of η-mesons. The current results at zero magnetic field can be compared with existing literature [35, 50, 60, 61]. In our previous study with zero magnetic field, we compared the results in detail and discovered that findings from different papers were in agreement for varying values of scattering length [36]. In addition to pure
$ \eta N $ interactions, the η meson mass-shift is assumed to be influenced by additional interactions, such as coupled channel effects. In relativistic mean field models, such as the chiral model, the self-energy is acquired by the meson-baryon interaction under a mean-field potential, whereas the coupled channel incorporates the full iteration of meson-baryon interactions, i.e., the T matrix. The coupled channel approach is utilized when two body meson-baryon interactions (i) are influenced by the intermediate resonances, and (ii) strongly interact with other meson-nucleon channels [50, 58]. For example, considering coupled channel effects, the$ \eta N $ interaction ($ U_{\eta N} $ = –34 MeV at$ \rho_N $ =$ \rho_0 $ ) is assumed to be influenced by$ N^* $ (1535) excitation [58]. However, the role of$ \eta \pi $ interactions in the in-medium mass-shift of η mesons have not been extensively studied in literature [100, 101]. In Ref. [100], the effect of$ \eta \pi $ interactions on η production is anticipated through the nuclear reaction$ \pi^- p \rightarrow \eta n $ , which is further utilized to calculate the$ \eta N $ scattering length$ a^{\eta N} $ . In the current study, we anticipated that the in-medium η meson mass shift decreases with an increase in the scattering length. Therefore, in future studies, it will be interesting to refine the chiral model calculations by including$ \eta \pi $ interactions and coupled channel effects. -
To summarize, we studied the effect of an external magnetic field on the in-medium mass of η-mesons in hot asymmetric nuclear matter. We studied in-medium
$ \eta N $ interactions using two separate methodologies. In the first approach, we computed the in-medium mass-shift of η-mesons using the chiral SU(3) model and observed a decrement in the effective mass as a function of the magnetic field and nuclear density. We anticipated substantial medium effects in the high magnetic field and density regime. In the second approach, we used the combined method of chiral perturbation theory (ChPT) and the chiral SU(3) model to compute the in-medium properties of η-mesons. In the latter approach, we introduced medium effects through the nucleon scalar density, which was calculated in the chiral SU(3) model. Using the joint approach, we found a substantial decrease in the mass of η-mesons regarding the magnetic field and nuclear density, which is much deeper than the observations from the first approach. The effects of isospin asymmetry and temperature are also incorporated and found to be slightly repulsive. In both approaches, we observed a direct dependence of the negative mass-shift with the$ a^{\eta N} $ scattering length. Furthermore, due to the zero charge on η mesons, we did not observe Landau quantization; therefore, no additional energy levels were discovered. The optical potential at finite momentum can be used to study experimental properties, such as momentum dependence [55, 62, 63] and the η-meson production rate [52-54] in the magnetized nuclear medium. Moreover, the observed negative mass-shift can be used to study the probability of$ \eta N $ bound state formation [34, 35]. To investigate eta-mesic nuclei at J-PARC, a high statistics search is proposed using the$ \pi $ beam [102]. There is also a proposal at the JLab (following the 12 GeV upgrade), to study the binding of Helium nuclei with ϕ and η mesons [103]. Additionally, the magnetic field influenced optical potential may be used in future experiments to study the in-medium observables of η-mesons [17]. -
One of the authors (R.K.) sincerely acknowledges the support for this study from the Ministry of Science and Human Resources Development (MHRD), Government of India, via the National Institute of Technology Jalandhar.
η mesons in hot magnetized nuclear matter
- Received Date: 2021-08-15
- Available Online: 2022-02-15
Abstract:





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: