-
The low-lying isomeric state
$ 3/2^+ $ $ (E_{\rm{is}}< 10 $ eV) in the$ ^{229} $ Th nucleus has garnered considerable interest owing to the possibility of designing the ultra-precise nuclear clock [1-4], the nuclear laser in the optical range [5, 6], and the nuclear light-emitting diode of the VUV range [7], as well as the study on a number of unusual processes: excitation and decay of$ ^{229m} $ Th by laser radiation via the electron shell at the electron bridge [8-15], control of the isomeric level$ \gamma $ decay via the boundary conditions [16] or chemical environment [17, 18],$ \alpha $ decay of the$ ^{229m} $ Th isomer [19] and accompanying bremsstrahlung [20], the relative effects of the variation of the fine structure constant and the strong interaction parameter [21-23], a check of the exponentiality of the decay law at long times [24], etc.The
$ ^{229m} $ Th isomeric state has the lowest excitation energy among all known nuclei. According to the latest data [25], its energy,$ E_{\rm{is}} $ , is$ 8.19\pm 0.12 $ eV. This result is approximately the value$ E_{\rm{is}} = 8.28 \pm 0.17 $ eV obtained in Ref. [26], the measurements of Ref. [27]$ E_{\rm{is}} = 8.10 \pm 0.17 $ eV, and$ E_{\rm{is}} = 7.8\pm 0.5 $ eV from Ref. [28]. Prior to that, for a fairly long period of time from 1990 to 2007, it was believed that$ E_{\rm{is}}<5 $ eV [29, 30].Currently, the
$ \alpha $ decay of$ ^{233} $ U is practically the only way to obtain the$ ^{229m} $ Th isomer. Effective excitation of$ ^{229m} $ Th via laser radiation is not feasible today, as it requires knowledge of the transition energy with a significantly greater accuracy than that achieved currently. Therefore, in [7], the excitation of$ ^{229m} $ Th via inelastic electron scattering was proposed. It was found that, in the beam energy region$ E\approx10 $ eV, the excitation cross section reaches the value of$ 10^{-25} $ cm$ ^2 $ . Such a large cross section indicates that the method of obtaining of$ ^{229m} $ Th using beams of negatively charged particles is promising. As a continuation of [7], we consider here the process of inelastic scattering of low-energy muons from the$ ^{229} $ Th nuclei.A prerequisite for such work may include the following considerations. In the Born approximation, cross sections for nuclear excitation to an isomeric state with the energy
$ E_{\rm{is}} $ were obtained analytically in Ref. [31] for the electric excitation and in Ref. [32] for the magnetic excitation. The cross sections for the magnetodipole ($ M1 $ ) transitions and electroquadrupole ($ E2 $ ) transitions take the form [31,32]$ \begin{aligned}[b]& \sigma^{\rm{Born}}_{M1} = \frac{16\pi^2}{9} e^2 \frac{2E-E_{\rm{is}}}{E}\ln{\frac{\sqrt{E}+\sqrt{E-E_{\rm{is}}}}{\sqrt{E}-\sqrt{E-E_{\rm{is}}}}} B(M1), \\ &\sigma^{\rm{Born}}_{E2} = \frac{64\pi^2}{225} e^2 m^2 \sqrt{\frac{E-E_{\rm{is}}}{E}} B(E2), \end{aligned} $

where
$ E = p^2/2m $ is the kinetic energy of a scattering particle with the mass$ m $ and momentum$ p = |{\bf{p}}| $ in the initial state of the nonrelativistic approximation, and$ B(M1) $ and$ B(E2) $ are the reduced probabilities of the nuclear transition from the ground state to the isomeric state.Based on the above formulas, the magnetic dipole cross section,
$ \sigma^{\rm{Born}}_{M1} $ , does not depend on the parameters of the scattered particle and is the same for electrons and muons. However, the cross section$ \sigma^{\rm{Born}}_{E2} $ includes the square of the mass of the scattered particle [31, 32]. Because the masses of the muon,$ m_{\mu} $ , and electron,$ m_e $ , are related as$ m_{\mu}/m_e\approx 206.77 $ , in the scattering of a muon and an electron of the same energy, we have$ \sigma^{\rm{Born}}_{E2}(\mu^-)/\sigma^{\rm{Born}}_{E2}(e^-)\approx 4\times 10^4 $ . If this relationship is retained in the low-energy region, then we can expect that the total$ M1+E2 $ cross section for the scattering of muons by the$ ^{229} $ Th nuclei will be several orders of magnitude larger than the cross section for scattering of slow electrons considered in [7].In this paper, we will consider the
$ ^{229} $ Th excitation by muons, calculate the cross section of the$ ^{229} $ Th$ (\mu^-,{\mu^-}) $ $ ^{229m} $ Th reaction for the low energy muons (we demonstrate that it is significantly larger than the cross section of the$ ^{229} $ Th$ (e^-,{e^-}) $ $ ^{229m} $ Th reaction), and discuss the new possibilities of studying the properties of the$ ^{229} $ Th nuclear transition$ 5/2^+(0.0)\leftrightarrow 3/2^+(8.19\pm0.12 $ eV) in the next generation of the muon colliders. -
The cross section of the nuclear excitation by muons (electrons) in the process illustrated in Fig. 1 was obtained in the framework of quantum electrodynamics in [7]. In the energy region where the kinetic energy of the muon in the initial state,
$ E = {\cal{E}}-m_{\mu} $ ($ {\cal{E}} $ is the relativistic energy$ {\cal{E}} = \sqrt{{\bf{p}}^2+m_{\mu}^2} $ ) satisfies the condition$ E \ll m_{\mu} $ , the cross section is given by$ \begin{aligned}[b] \sigma_{E(M)L} =\ & 4e^2\lambda^2_{\gamma_{\rm{is}}} \left(\frac{E}{E_{\rm{is}}}\right)^{-3/2} \left(\frac{E}{E_{\rm{is}}}-1\right)^{-1/2} \frac{B(E(M)L;J_i\rightarrow{}J_f)}{a_{\rm B}^{2L}} \\ &\times \sum_{l_i,j_i \atop{}l_f,j_f} \frac{(2l_i+1)(2j_i+1)(2j_f+1)}{(2L+1)^2} \left(C^{l_f0}_{l_i0L0}\right)^2 \left\{ \begin{array}{ccc} l_i & L & l_f \\ j_f &1/2& j_i \end{array} \right\}^2 \left|{\tilde{{{m}}}}^{E(M)L}_{fi}\right|^2, \end{aligned} $ 
(1) where
$ \lambda_{\gamma_{\rm{is}}} = 2\pi/E_{\rm{is}} $ is the wavelength of the isomeric nuclear$ \gamma $ transition,$a_{\rm B}$ is the Bohr radius,$a_{\rm B} = 1/(e^2m_e)$ ,$ e $ and$ m_e $ are the charge and mass of the electron, and$ j_{i,f} $ and$ l_{i,f} $ are the total and orbital angular momenta of the muon in the initial and final states, respectively. In the case of the$ ML $ transition, one replaces$ l_i $ by$ l'_i = 2j_i-l_i $ . The muon matrix elements in Eq. (1) are$ \begin{aligned}[b] &{\tilde{{{m}}}}_{fi}^{EL} = \int_0^{\infty} [g_i(x)g_f(x)+ f_i(x)f_f(x)]\frac{{\rm d}x}{x^{L-1}},\\ & {\tilde{{{m}}}}_{fi}^{ML} = \frac{\kappa_i+\kappa_f}{L} \int_0^{\infty}[g_i(x)f_f(x)+f_i(x)g_f(x)]\frac{{\rm d}x}{x^{L-1}}, \end{aligned} $

(2) where
$x = r/a_{\rm B}$ [hence, in Eqs. (1)–(2) and in the Dirac equations, the Bohr radius$a_{\rm B}$ is adopted as a natural parameter characterizing the size of the electron shell of the Thorium atom (ion)]. Here the large,$ g(x) $ , and the small,$ f(x) $ , components of the Dirac wave function are the solution of the Dirac equations with the interaction potential$ V(x) $ :$ \begin{aligned}[b] &g'(x)+\frac{1+\kappa}{x}g(x)- \frac{1}{e^2}\left(\frac{{\cal{E}}}{m_e}+\frac{m_{\mu}}{m_e}-\frac{V(x)}{m_e}\right)f(x) = 0,\\ &f'(x)+\frac{1-\kappa}{x}f(x)+ \frac{1}{e^2}\left(\frac{{\cal{E}}}{m_e}-\frac{m_{\mu}}{m_e}-\frac{V(x)}{m_e}\right)g(x) = 0. \end{aligned} $

(3) The function
$ g(x) $ in Eq. (3) is normalized at$ x\rightarrow\infty $ with the condition$g(x) = \sin(pa_{\rm B}x+\varphi_{lj})/x$ , where$ \varphi_ {lj} $ is a phase,$ \kappa = l(l+1)-j(j+1)-1/4 $ .The total potential of the nucleus and the electron shell was built in the standard way, described in detail in [7, 33]: the nucleus was taken in the form of a uniformly charged ball of radius
$ R_0 = 1.2A^{1/3} $ fm, where$ A $ is the atomic number, and the electron shell was calculated within the DFT theory [34, 35] via the self-consistent procedure. After that, the potential was obtained as a result of the double integration of the electron density.The excitation by muons has its own characteristics. The wave function of a scattering muon, in comparison with the wave function of a scattered electron, has a significantly larger amplitude in the region of the nucleus (see examples of wave functions in Fig. 2). However, the wavelength of the muon is substantially shorter than the wavelength of the electron, and the muon wave function oscillates more rapidly. Therefore, the muon matrix element is formed in a significantly smaller region than that of the electron. The calculations indicate that the muon matrix element reaches a plateau at
$r\approx5R_0\approx 0.007a_{\rm B}$ , while the electron matrix element is formed in the region$r\lesssim 0.1a_{\rm B}$ [7]. Owing to this compensation, the muon and electron matrix elements in the case of the$ M1 $ excitation end up being close in magnitude. Consequently, the cross sections for the magnetic dipole excitation of the$ ^{229m} $ Th isomer by the low-energy muons and electrons are comparable in magnitude (see below in Fig. 3).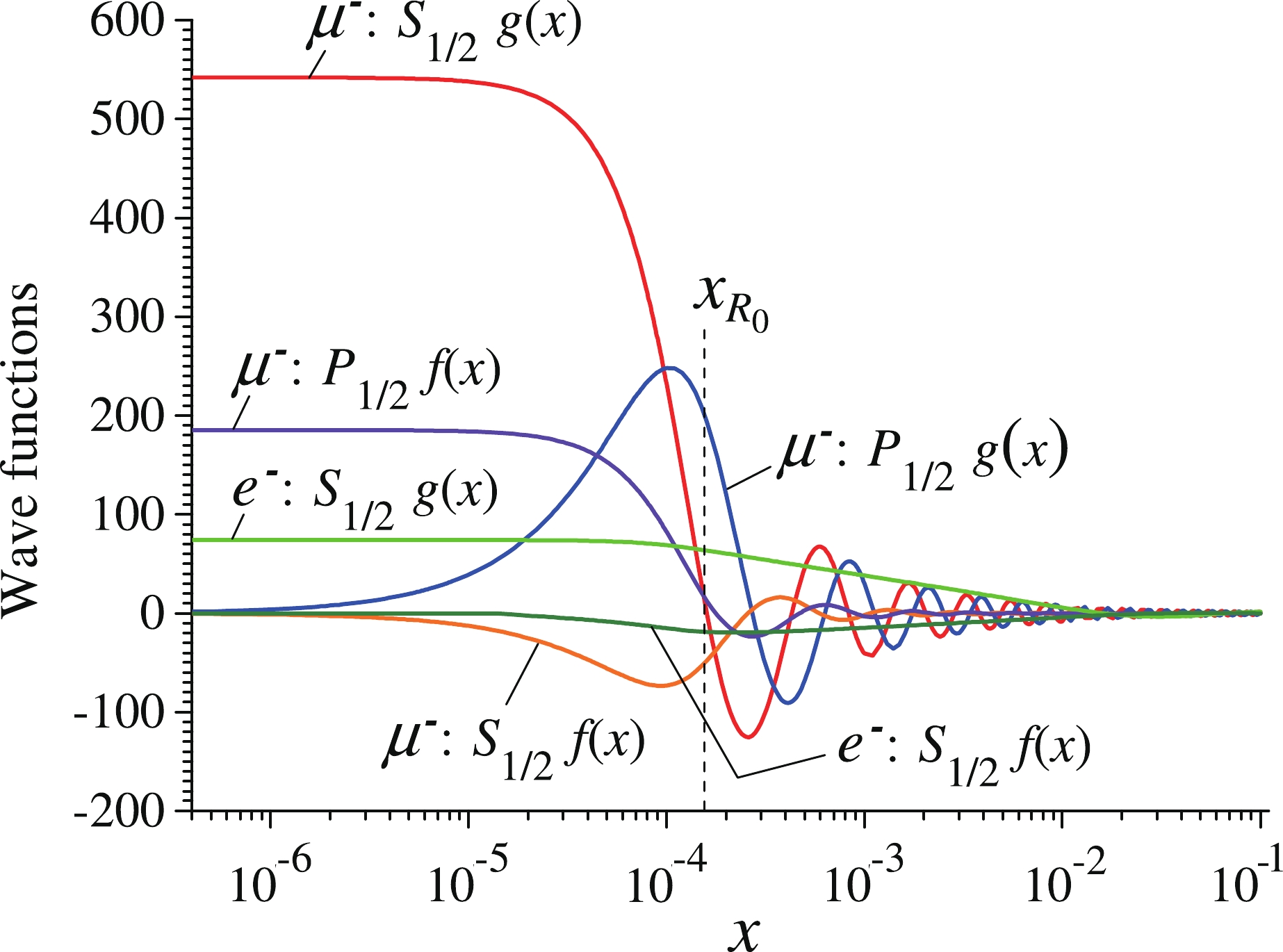
Figure 2. (color online) Wave functions of scattered muons and electrons with the energy
$E=10$ eV in the potential of the Th atom. Here,$x_{R_0}=R_0/a_{\rm B}$ is a nuclear radius in units of$a_B$ .
Figure 3. (color online) Total and partial E2E2 cross sections for the
$^{229}$ Th$(\mu^-,\mu^-)^{229m}$ Th reaction for$B_{\rm{W.u.}}(E2;3/2^+\rightarrow $ $ 5/2^+)=11.7$ . For comparison, the total$M1$ cross section for$B_{\rm{W.u.}}(M1; 3/2^+\rightarrow 5/2^+)=0.031$ and the total$M1+E2$ electron cross section from [7]$\sigma_e$ (Th0) are shown.The situation is different for the
$ E2 $ excitation. The factor$ 1/x^{L-1} $ in Eq. (2) at$ L = 2 $ enhances the contribution to the matrix element from the small$ x $ region. However, inside the nucleus, the amplitudes of the muon wave functions exceed the amplitudes of the electron wave functions by an order of magnitude. This explains the significant increase in the cross section for the electroquadrupole excitation of the$ ^{229m} $ Th isomer by muons in comparison with electrons. -
The calculation results of the
$ ^{229m} $ Th isomer excitation cross section by muons are presented in Fig. 3 and Fig. 4. As expected, the cross section for the magnetic dipole excitation turned out to lie close in magnitude (within an order of magnitude) to the electron cross section from [7] and is approximately four orders of magnitude smaller than the cross section for the electroquadrupole excitation, Fig. 3. This is an interesting and useful observation, which allows us to extract the value of the reduced probability of the$ E2 $ nuclear transition$ B_{\rm{W.u.}}(E2,5/2^+\rightarrow 3/2^+) $ from the$ ^{229} $ Th$ (\mu^-,\mu^-)^{229m} $ Th reaction.
Figure 4. (color online) Cross sections of the E2 excitation of the
$^{229m}$ Th isomer by muons in the Thorium atom (Th0) and Thorium ions Th+ and Th4+.The total excitation cross sections of the
$ ^{229m} $ Th isomer for two selected values of the reduced probability of the nuclear$ E2 $ transition$ 3/2^+\rightarrow 5/2^+ $ are shown in Fig. 4. The first value,$ B_{\rm{W.u.}}(E2;3/2^+\rightarrow 5/2^+) = 11.7 $ , is an average over four experimental measurements [36-39] of the$ E2 $ transitions between the$ 3/2^+[631] $ and$ 5/2^+[633] $ rotation bands in the$ ^{229} $ Th nucleus found with Alaga rules in Ref. [40]). The second value,$ B_{\rm{W.u.}}(E2;3/2^+\rightarrow 5/2^+) = 27 $ , was obtained theoretically in Ref. [41], as a result of the computer calculations within the modern nuclear models.Let us estimate the possible rate of excitation of the isomeric nuclei by
$ \mu^- $ . As can be observed from the graphs in Fig. 4, for the problem under consideration, muons with energies 10–100 eV are the most interesting, because the excitation cross sections of the isomer have the values$ 10^{-21} $ –$ 10^{-22} $ cm$ ^2 $ in this energy range.A
$ \mu^- $ beam slowed down to these energies was obtained in [42]. Measurement of the stopping power indicated that the absorption of$ \mu^- $ is very small in the range$ E = 10 $ –100 eV [42]. This is an interesting result. This implies that below the peak at approximately 10 keV,$ \mu^- $ becomes too slow to ionize atoms [43], and the stopping power is induced by elastic collisions between the projectiles and the target nucleus [44]. The isomer excitation reaction considered in this work is an additional channel for the scattering process on nuclei, and it will proceed in parallel with the elastic collision.An important question is as follows: how many negative muons will survive at the required stage of deceleration. It is well known [43] that in the energy range
$ E\lesssim 5 $ keV, the dominant process is that in which the$ \mu^- $ takes an atomic orbit around a nucleus, yielding the muonic atom. A negative muon captured on the atomic shell can excite the$ ^{229} $ Th nucleus to high-lying levels in a cascade of bound states transitions, provided that there is a coincidence in energy and multipolarity between the nuclear and muonic transitions [45].In [42], Kapton was adopted as a moderator for decelerating negative muons to several eV. Consequently, some of the muons avoided being captured by its atoms, were slowed down to energies of the eV range by passing through a Kapton layer of the thickness
$ 1.3\times10^{-4} $ cm. Then the beam of slow muons was directed to the Au/Pd target, where the muons were gradually stopped and captured by the target. In the range$ E\leq 100 $ eV, the stopping power was$ \simeq1 $ eV$ \, $ Å$ ^{-1} $ [46]. Therefore, the Au/Pd target thickness of approximately 7 nm was selected; hence, the main parts of the slow muons stopped and were captured by the Au/Pd atoms. In accordance with the above estimates, the optimal thorium target thickness$ h $ should be in the range 1–10 nm.The fraction of slow muons
$ \xi $ was approximately$ 10^{-4} $ –$ 10^{-5} $ , relative to the particles of the initial beam with$ E = 54 $ MeV in [42]. Such a small value is explained by the fact that the authors selected$ \mu^- $ according to the direction of motion and the value of energy. Accordingly, a beam of muons moving in one direction, which has a narrow energy distribution, was produced. To excite$ ^{229} $ Th nuclei, the creation of a narrow directed monochromatic beam is not required. Hence, if we consider all muons that passed through the Kapton (i.e., all directions and all energies), the value of$ \xi $ will increase by two–three orders of magnitude in comparison with the quoted value of [42].The nuclear isomer
$ ^{229m} $ Th is registered using internal conversion electrons with an efficiency$ \eta $ of approximately 1 [47, 26]. For estimates, we also take the most intense modern source of muons (muon factory), which gives currents$ j_{\mu}\approx 4\times 10^8 $ s$ ^{-1} $ (i.e. 0.064 n$ A $ ) [48].The rate of
$ \mu^- $ excitation of the isomeric nuclei in the metallic target of the thickness$ h = 1 $ –10 nm from the isotopically pure$ ^{229} $ Th, with the density of nuclei$ \rho_{\rm{Th}} = 3\times10^{22} $ cm$ ^{-3} $ , can be estimated by the formula$ {\rm d} N_{\rm{is}}/{\rm d}t \approx{} \eta \rho_{\rm{Th}} h\, \xi\, j_{\mu} \sigma_{E2} \simeq 10^0{\rm-}10^3\,\, {\rm{s}}^{-1}. $

The first value
${\rm d}N_{\rm{is}}/{\rm d}t \approx 1$ s$ ^{-1} $ corresponds to the most pessimistic scenario, while the second (${\rm d}N_{\rm{is}}/{\rm d}t \approx $ $ 10^3$ s$ ^{-1} $ ) corresponds to the most optimistic one.Note that in the electronic and muonic scattering experiments, it is unnecessary to precisely tune the muon energy and know the energy of the nuclear isomeric level
$ E_{\rm{is}} $ with high accuracy, because the excitation process is non-resonant. -
In conclusion, the cross section for the excitation of the anomalous low-lying
$ (3/2^+,8.19\pm0.12 $ eV) level in the$ ^{229} $ Th nucleus by low-energy muons was calculated. It was demonstrated that a) the muon cross section is four or five orders of magnitude larger than the electron one, and b) in the region$ E\approx 10 $ eV, the muon cross section of the electroquadrupole excitation reaches the value of$ 10^{- 21} $ cm$ ^2 $ and is approximately four orders of magnitude larger than that of the muon magnetodipole excitation. The dominance of the Coulomb$ E2 $ excitation at the muon scattering makes it possible for the next generation of the muon colliders to extract the value of the nuclear matrix element of the$ E2 $ transition from the scattering data and test some aspects of existing theoretical models for the isomeric state.
Cross section of the Coulomb excitation of ${^{\boldsymbol{229m}}{\bf{Th}}} $ by low energy muons
- Received Date: 2021-05-13
- Available Online: 2021-09-15
Abstract: The inelastic scattering cross section for muons,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: