-
High-energy nuclear collisions at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) provide an excellent arena to unravel the properties of quark-gluon plasma (QGP), a new state of nuclear matter with de-confined quarks and gluons, which is predicted to be formed in extreme hot and dense system by quantum chromodynamics (QCD), the fundamental theory of strong interaction. In the past few decades, the "jet quenching" phenomenon, the energy loss of the initially produced energic jet due to strong interactions with the constituents of QGP has garnered great interest from physicists and has been extensively studied [1-18]. These studies show that the differences between the final-state observables at large transverse momentum, such as leading hadron spectra and jet production, in p+p and A+A collisions can help us gain insight into the mechanisms of in-medium parton interactions and precisely extract valuable information on the properties of QGP created in relativistic heavy-ion collisions.
Owing to their large mass (
$ M_Q\gg T $ ) and early creation time, heavy quarks are witnesses of the entire QGP evolution and are therefore viewed as ideal hard probes to constrain the transport properties of QGP and also improve our understanding of in-medium heavy quark evolution. As new favorites of observables in heavy-ion collisions (HIC), the nuclear modification factor$ R_{AA} $ [19-21], collective flow$ v_n $ [22-25] of heavy flavored mesons, and$ D^0 $ + hadron correlations [26] have been extensively measured experimentally and successfully modeled in theory [27-45]; however, there are still some important key questions to be addressed [46]. For reviews, see Refs. [46-51].The recent measurements relating to the production and substructure of heavy flavor jets shed new light on the jet physics in high-energy heavy-ion collisions [52-54], aiming to address the mass effect on in-medium jet shower evolution. Among them, the nuclear modification factors
$ R_{pA} $ [55,56] and$ R_{AA} $ [52] of heavy flavor jets offer strong tools for quantifying the cold nuclear matter (CNM) effects in the initial-state and the in-medium quenching effects in the subsequent formed QGP [57-61]. In particular, the recently reported radial distributions of charm mesons in jets by the CMS collaboration provide an interesting opportunity to investigate the diffusion effects of heavy quarks as well as the modified substructure of heavy flavor jets in nucleus-nucleus collisions from a new angle [54], and a detailed discussion on c-jets was presented in our previous work [61]. As bottom quarks have larger mass than charm quarks ($ m_{b}\sim 4.5 $ GeV,$ m_{c}\sim 1.5 $ GeV), the radial profiles of bottom quarks in jets can be new signals to gain insight into the in-medium partonic interaction and mass effects. Therefore, it will be interesting and urgent to investigate the radial distribution of bottom quarks in jets in p+p collisions and its modification in nucleus-nucleus collisions.In this work, we present the first theoretical study on the radial distribution of bottom quarks in jets in heavy-ion collisions. A systematic comparison between the radial profiles of bottom and charm quarks in jets is also investigated, aiming to reveal the sensitivity of quark mass to heavy quark diffusion effects. We employ a Monte Carlo event generator, SHERPA [62], at next-to-leading order QCD calculations matched with parton shower (NLO+PS) accuracy as the p+p baseline, and also take into account the in-medium elastic and inelastic parton energy loss. In p+p collisions, we find that the radial profiles of heavy quarks in jets are sensitive to the heavy quark mass. In 0-10% Pb+Pb collisions at
$ \sqrt{s_{NN}} = 5.02 $ TeV, we observe an inverse modification pattern of the radial profiles of bottom quarks in jets compared to those of charm quarks: jet quenching effects will narrow the jet radial profiles of bottom quarks while broadening those of charm quarks. We demonstrate that the different modification patterns are mainly determined by their initial radial distributions in jets.The remainder of this paper is organized as follows. In Sec. II, we present the radial distributions of bottom quarks in jets in p+p collisions compared to charm quarks. In Sec. III, the Monte Carlo framework of the in-medium jet evolution is introduced. Discussions on the medium modification of the bottom quark radial profiles in jets are given in Sec. IV. We summarize this paper in Sec. V.
-
The production of heavy flavor jets (charm jets and bottom jets, usually denoted as c-jets and b-jets) in high energy physics has been extensively studied both as tests of perturbative QCD calculation [63] and as probes for other physics aspects within and beyond the Standard Model [64]. Heavy quark jets are defined as the jets containing heavy quarks (heavy flavor mesons) inside the jet. In general, the production mechanisms of heavy flavor jets in hadron collisions are often attributed to three categories: flavor creation (FCR), flavor excitation (FEX), and gluon splitting (GSP) [64,65]. FCR represents the
$ Q\bar{Q} $ pair creation process at leading order ($ q+\bar{q}\rightarrow Q+\bar{Q} $ ,$ g+g\rightarrow Q+\bar{Q} $ ) in hard scattering. FEX is the process in which a heavy quark from the initial parton distribution of one beam particle is excited onto the mass shell by hard scattering by a parton of the other beam particle. GSP is the situation in which$ g\rightarrow Q+\bar{Q} $ branching occurs in the initial or final state parton shower, but does not involve hard scattering. In this work, the heavy flavor jet production in p+p collisions is provided by the Monte Carlo event generator SHERPA [62], in which the NLO QCD matrix elements are matched with parton showers (PS) availably [66]. An NNPDF3.0 [67] NLO parton distribution function (PDF) with a massive bottom quark was chosen in the calculations. The final-state jet reconstruction and event selection are implemented with an anti-$ k_T $ algorithm [68] within the Fastjet package [69]. In our current study, the fragmentation of heavy quarks ($ c\rightarrow D $ ,$ b\rightarrow B $ ) is performed by introducing the Peterson form fragmentation functions (FFs) [70]$ D(z)\propto1/z(1-1/z-\epsilon/ $ $ (1-z))^2 $ , where$ \epsilon_c = 0.01, \epsilon_b = 0.001 $ [71-73]. According to the estimates in Ref. [34], the in-medium coalescence mechanism has less influence on the heavy quarks with$ p_T>4\; $ GeV.In Fig. 1, we present the calculation results of radial distributions of B mesons in jets in p+p collisions at
$ \sqrt{s_{NN}} = 5.02 $ TeV at three transverse momentum regions of B mesons ($ 4<p_T^Q<20 $ GeV,$ 20<p_T^Q<40 $ GeV,$ 40<p_T^Q<60 $ GeV) compared with the case of D mesons in jets.$ r = \sqrt{(\Delta\phi_{JQ})^2+(\Delta\eta_{JQ})^2} $ is defined by the relative azimuthal angle$ \Delta\phi_{JQ} $ and relative pseudorapidity$ \Delta\eta_{JQ} $ between the heavy quark meson and the jet axis; please note that the superscript and subscript$ Q $ denotes a heavy quark meson. All the selected B meson+jets and D meson+jets are reconstructed by an anti-$ k_T $ algorithm with$ R = 0.3 $ within$ |\eta^{\rm jet}|<1.6 $ and are required to have$ p_T^{\rm jet}>60 $ GeV.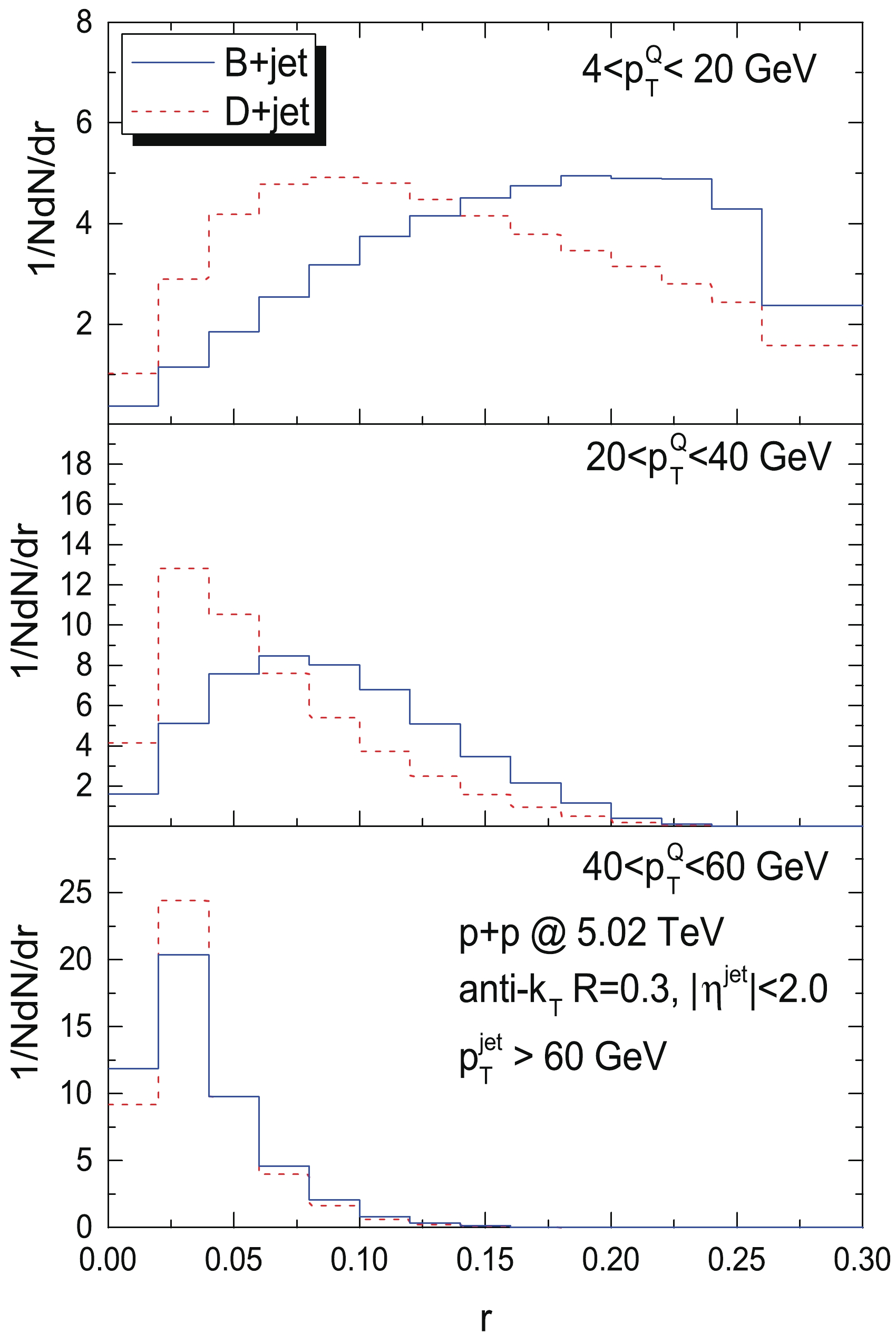
Figure 1. (color online) Normalized radial distributions of B mesons and D mesons in jets as functions of the angular distance to the jet axis in p+p collisions at 5.02 TeV simulated by SHERPA. Three
$ p_T $ regions of heavy quark mesons are plotted in the top, middle, and bottom panels: 4-20 GeV, 20-40 GeV, and 40-60 GeV, respectively.When we compare the radial distribution of the same heavy flavor in jets at different
$ p_T^Q $ regions of the final state heavy flavor meson, we find a narrower distribution of radial profile with increasing$ p_T^Q $ both for B mesons and D mesons in jets. We also find a discrepancy in the radial profile distributions of B mesons and D mesons in jets at the same$ p_T^Q $ region, especially at$ 4<p_T^Q<20 $ GeV; the B mesons distributed at larger$ r $ peak around$ r = 0.20 $ and D mesons distributed at smaller$ r $ peak around$ r = 0.07 $ as shown in the top plots of Fig. 1. With the enhancement of the$ p_T^Q $ region, this kind of discrepancy tends to disappear as demonstrated in the bottom plots of Fig. 1. By simply changing the value of the quark mass in the calculation in p+p, we confirm the distinct radial profile distributions all arise from the difference of heavy quark masses. Obviously the$ 4<p_T^Q<20 $ GeV region of the final state heavy flavor meson provide a unique opportunity to investigate the potential different in-medium modifications of B mesons and D mesons in jets, and we also need to keep in mind the$ p_T^Q $ trigger sensitivity of the radial profile distribution of heavy flavors in jets for further discussion. -
To implement the in-medium parton evolution for light partons and heavy quarks simultaneously, we use the p+p events generated by SHERPA [62] with a vacuum parton shower as input, and then investigate the subsequent in-medium jet evolution in hot and dense QCD matter with the Simulating Heavy quark Energy Loss with Langevin equations (SHELL) model [60,61,74,75].
In the SHELL model, the initial spatial distribution of partons is sampled by a Monte Carlo Glauber model [76]. When a parton propagates in QGP, two important energy loss mechanisms are considered: collisional interaction (elastic scattering with the constituents of the medium) and radiative interaction (medium-induced gluon radiation in inelastic scattering). In the infinite heavy quark limit (
$ p \sim T $ ,$ M\gg T $ ), the propagations of heavy quarks in QGP are usually well described by the Langevin equations. When it goes to the higher$ p_T $ region, as the medium-induced gluon radiation become the dominant mechanism for heavy quark energy loss, the modified Langevin equations [34,60,61,74,75] are viewed as an effective method to take into account the radiative correction, as shown in Eq. (2):$ \vec{x}(t+\Delta t) = \vec{x}(t)+\frac{\vec{p}(t)}{E}\Delta t , $

(1) $ \vec{p}(t+\Delta t) = \vec{p}(t)-\Gamma(p)\vec{p} \Delta t+\vec{\xi}(t)-\vec{p}_g \, , $

(2) where
$ \Delta t $ is the time step of the in-medium Monte Carlo simulation, and$ \Gamma $ is the drag coefficient.$ \vec{\xi}(t) $ is white noise representing the random kicks obeying$ \left \langle \xi^i(t)\xi^j(t') \right \rangle = \kappa \delta^{ij}\delta(t-t') $ , where$ \kappa $ is the diffusion coefficient in momentum space.$ \Gamma $ and$ \kappa $ are usually associated by the fluctuation-dissipation relation$ \Gamma = \dfrac{\kappa}{2ET} = \dfrac{T}{D_s E} $ , where$ D_s $ , the spatial diffusion coefficient, is viewed as a free parameter estimated in various theories [77]. In this study, we choose$ D_s = \dfrac{4}{2\pi T} $ extracted by lattice QCD [78,79] as a fixed parameter in our calculations. The last term in Eq. (2) represents the momentum recoil due to the medium-induced gluon radiation, which is implemented based on the higher-twist calculations [80-83]:$ \frac{{\rm d}N}{{\rm d}x{\rm d}k^{2}_{\perp}{\rm d}t} = \frac{2\alpha_{s}C_sP(x)\hat{q}}{\pi k^{4}_{\perp}}\sin^2 \left(\frac{t-t_i}{2\tau_f}\right) \left(\frac{k^2_{\perp}}{k^2_{\perp}+x^2M^2}\right)^4 , $

(3) where
$ x $ and$ k_\perp $ are the energy fraction and transverse momentum carried by the radiated gluon.$ C_s $ is the quadratic Casimir in color representation,$ P(x) $ is the splitting function in a vacuum [84], and$ \tau_f = 2Ex(1-x)/ $ $ (k^2_\perp+x^2M^2) $ is the gluon formation time.$ \hat{q} \propto q_0(T/T_0)^3 $ is the jet transport parameter [85], where$ T_0 $ is the highest temperature in the most central A+A collisions. Note that we use the same value$ q_0 = 1.2 $ GeV$ ^2 $ /fm, determined by a global extraction of the single hadron production in Pb+Pb collisions at the LHC energy [86], to describe the strength of gluon radiation for all partons; the mass effects of heavy quarks are included in the last quadruplicate term in Eq. (3).In the consideration of possible multiple gluon radiation during a time step of our simulation, we assume that the number of radiated gluons obeys the Poisson distribution:
$ \begin{array}{l} P(n) = \dfrac{\lambda}{n!} {\rm e}^{-\lambda} , \end{array} $

(4) where
$ P(n) $ denotes the probability of$ n $ instances of radiative interaction during a short time step$ \Delta t $ , and$ \lambda $ is the mean value of$ n $ and could be estimated numerically by integrating Eq. (3):$ \lambda(t,\Delta t) = \Delta t\int {\rm d}x {\rm d} k^2_{\perp} \frac{{\rm d}N}{{\rm d}x {\rm d}k^2_{\perp} {\rm d}t} . $

(5) During each time step in our simulation, first, the total probability
$ P(n\geqslant 1) = 1-\lambda {\rm e}^{-\lambda} $ is calculated to determine whether radiation occurs. If radiation occurs, the number of radiated gluons could be sampled based on Eq. (4), and subsequently the four momentum of each gluon can be sampled by Eq. (3) one-by-one. It should be noted that a lower cutoff$ \omega_0 = \mu_D = \sqrt{4\pi\alpha_s}T $ has been imposed to avoid the divergence in the spectra at$ x\rightarrow 0 $ , namely only a gluon with energy above this cutoff is allowed to be emitted. This treatment could mimic the detailed balance between gluon radiation and absorption, and then ensure heavy quarks can achieve their thermal equilibrium,$ f_{eq}(p)\propto {\rm e}^{-E(p)/T} $ after sufficient propagating time in the QGP medium. The hydrodynamic background profile of the expanding QCD medium is provided by the smooth (2+1)D viscous hydrodynamic model [87]. We assume that partons stop in-medium propagation when their local temperature is under$ T_c = 165 $ MeV. To take into account the initial-state CNM effects in nucleus-nucleus collisions, the nuclear parton distribution function (nPDF) nNNPDF1.0 [88] has been used in the calculations. It is found that the CNM effects have little impact on the radial profiles of heavy quarks in jets.The SHELL model has been applied in studies of medium modification of
$ p_T $ imbalance of$ b\bar{b} $ dijets [60] and correlations of$ Z^0 $ + b-jets [75]. Recently, it has also been successfully employed to calculate the angular correlations of$ D^0 $ + jet in p+p and Pb+Pb collisions at$ \sqrt{s_{NN}} = 5.02\; $ TeV [61,74], and a decent agreement between the model calculations and experiment measurements has been observed [54]. -
The in-medium parton interactions not only dissipate the jet energy to the hot and dense QCD matter outside the jet cone, subsequently suppressing the jet production, but also redistribute the energy-momentum of partons inside the jet cone, thus altering the jet radial profile and the jet substructure. The modified radial distribution of low
$ p_T $ heavy quarks relative to their tagged high$ p_T $ jets, which act as a reference, could indirectly reflect the dynamical details of in-medium parton interactions in hot and dense nuclear matter. In this section, systematic predictions of the radial profile of B mesons in jets both in p+p and Pb+Pb collisions are presented, and further the comparison between bottom and charm flavors in jets is also investigated aiming to figure out the impact of the mass effect to the medium modification pattern of the radial profile.In Fig. 2, we predict the B meson radial distribution in jets in central 0-10% Pb+Pb collisions at
$\sqrt{s_{NN}} = 5.02$ TeV compared to its p+p baseline. In both p+p and Pb+Pb collisions, the selected jets are required to have$ p_T^{\rm jet}>60 $ GeV and be tagged by at least one B meson with$ 4<p_T^Q<20 $ GeV, which is the same as in our previous study [61] and the CMS measurements [54] on the case of D mesons in jets. In the top plots in Fig. 2, we observe the B meson radial distribution in jets in Pb+Pb shifting towards smaller radii relative to its p+p baseline, thus finding enhancement at smaller radii and suppression at larger radii in the ratio of the normalized radial distribution in Pb+Pb to that in p+p shown in the lower panel of Fig. 2. However, this kind of modification to a narrower radial profile is in contrast to the toward broader medium modification pattern of the D meson radial profile in jets predicted and measured in [54,61]. It is not intuitive to picture the charm quarks shifting towards larger radii while the bottom quarks shift close to the jet axis due to an identical in-medium parton interaction mechanism without further investigation. An additional interesting question will be raised: what role is played by the different masses of bottom and charm quarks in jets?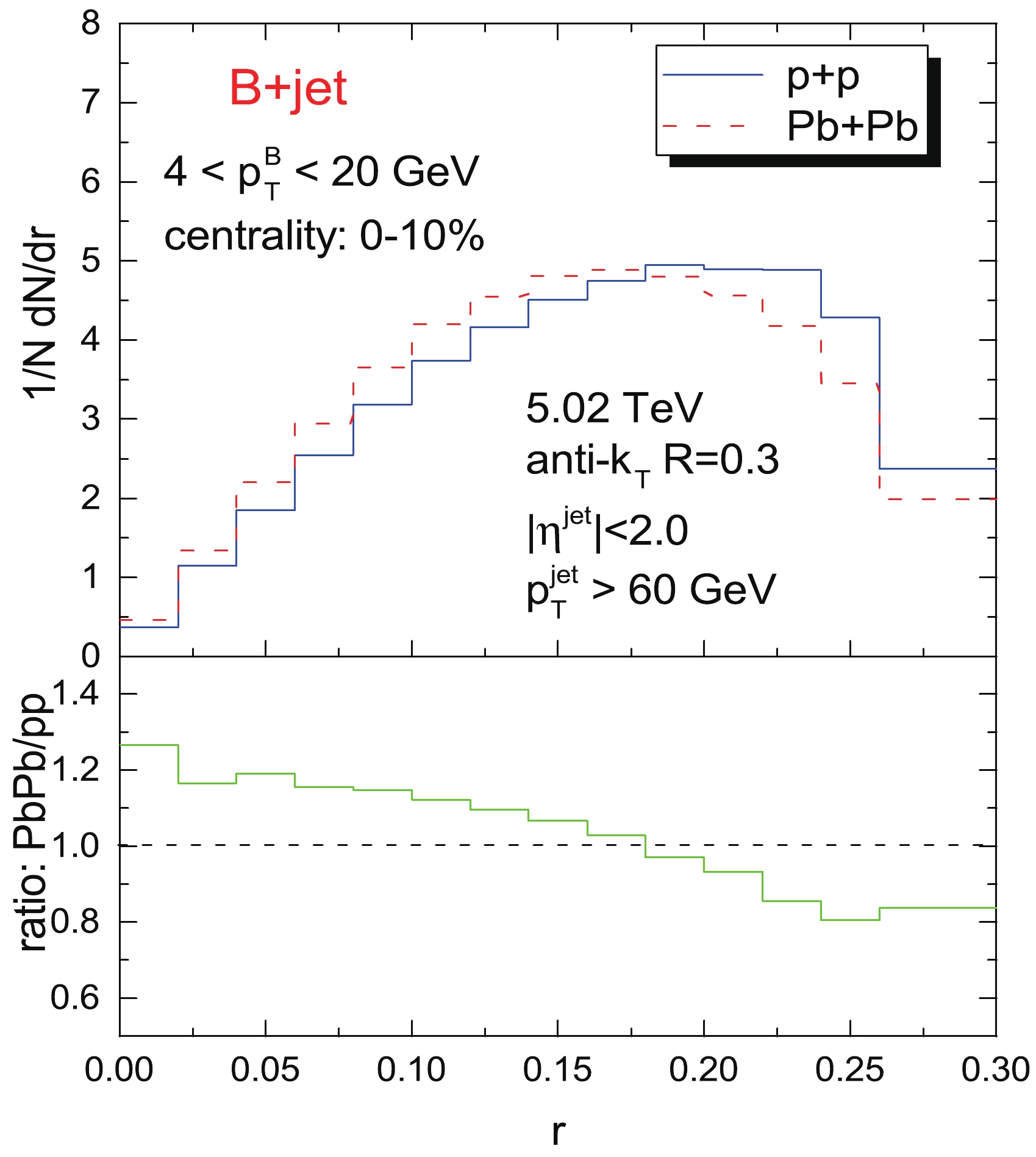
Figure 2. (color online) Normalized radial distributions of B meson in jets as a function of the angular distance to the jet axis in p+p and 0-10% Pb+Pb collisions at
$ \sqrt{s_{NN}} = 5.02 $ TeV. The ratio of the normalized distribution in Pb+Pb to that in p+p is also plotted in the lower panel.To conduct such an investigation, it is instructive to first clarify the compositions of the jets reconstructed in Pb+Pb collisions. Please note the reconstructed jets in Pb+Pb collisions also obey the selection of
$ 4<p_T^Q<20 $ GeV, as for the p+p baseline. Therefore, one can easily imagine that some of the reconstructed jets in Pb+Pb could be the surviving ones for which$ p_T^Q $ does not fall below the lower threshold of$ 4 $ GeV due to jet quenching; these surviving jets do have their original counterparts in the p+p baseline events before jet quenching with$ 4<p_T^Q<20 $ GeV. However, a lot of the jets reconstructed in Pb+Pb are those with heavy flavor mesons$ p_T^Q>20 $ GeV before jet quenching. These parts of the jets reconstructed in Pb+Pb do not have their counterparts in the p+p baseline events and are initially (originally) distributed closer to the jet axis than the case of p+p baseline events simply because of the higher$ p_T^Q $ trigger according to the discussion of Fig. 1. To facilitate further discussion, we name these two contribution sources the Survival part and the Transfer part. The separation and the respective investigations of the two contribution sources are not easy for analytical or experimental study; the sources tracking power of our Monte Carlo study can help us to do so and therefore gain more insight of the medium modification mechanism of the heavy flavor radial profiles in jets.Contribution fraction is essential when talking about the relation between the overall modification and respective modification of each composition. In Fig. 3 we plot the contribution fractions of the Survival part and Transfer part in the reconstructed jets in Pb+Pb as a function of
$ r $ for both D mesons and B mesons in jets, respectively. We find that in the$ 4<p_T^Q<20 $ GeV region we investigated, for both cases of D mesons and B mesons in jets, the Transfer part denoted by short dash lines dominates at smaller$ r $ , and the domination begins to decrease with increasing$ r $ . We can observe that the charm quark suffers more energy dissipation than the bottom quark in this context, as at any$ r $ there is always a higher surviving proportion of bottom quarks; even at larger$ 0.25<r<0.3 $ , the survival part begins to dominate.
Figure 3. (color online) Fractional contribution of the reconstructed event from the Survival part and Transfer part in the B meson and D meson radial distributions in jets at
$ 4<p_T^Q<20 $ GeV in 0-10% Pb+Pb collisions at$ \sqrt{s_{NN}} = 5.02 $ TeV.With such knowledge of the contribution fractions of the two parts in Pb+Pb events, we plot in Fig. 4 the modification patterns of B meson radial profiles in jets in the top panel and the case for D meson radial profiles in jets in the bottom panel. In these plots, we also include the ratios of the self-normalized radial distribution of the Survival and Transfer contribution parts in Pb+Pb to the normalized p+p baseline denoted as a dash dotted line and short dashed line, respectively. First, we confirm an inverse medium modification pattern of the radial profile of the heavy flavor in jets when comparing the total normalized distribution PbPb/pp ratios as functions of
$ r $ of B+jet (solid line in the top panel) and D+jet (solid line in the bottom panel). The total normalized distribution PbPb/pp ratio is combinated by the Survival and Transfer contributions taking into account their contribution fractions. Since at smaller$ r $ region the Transfer part dominates the contribution fraction, the modification pattern of the Transfer part is dominant, but in the larger$ r $ region, the contribution fraction interplays with the respective ratios of the two contribution parts to determine the total ratio.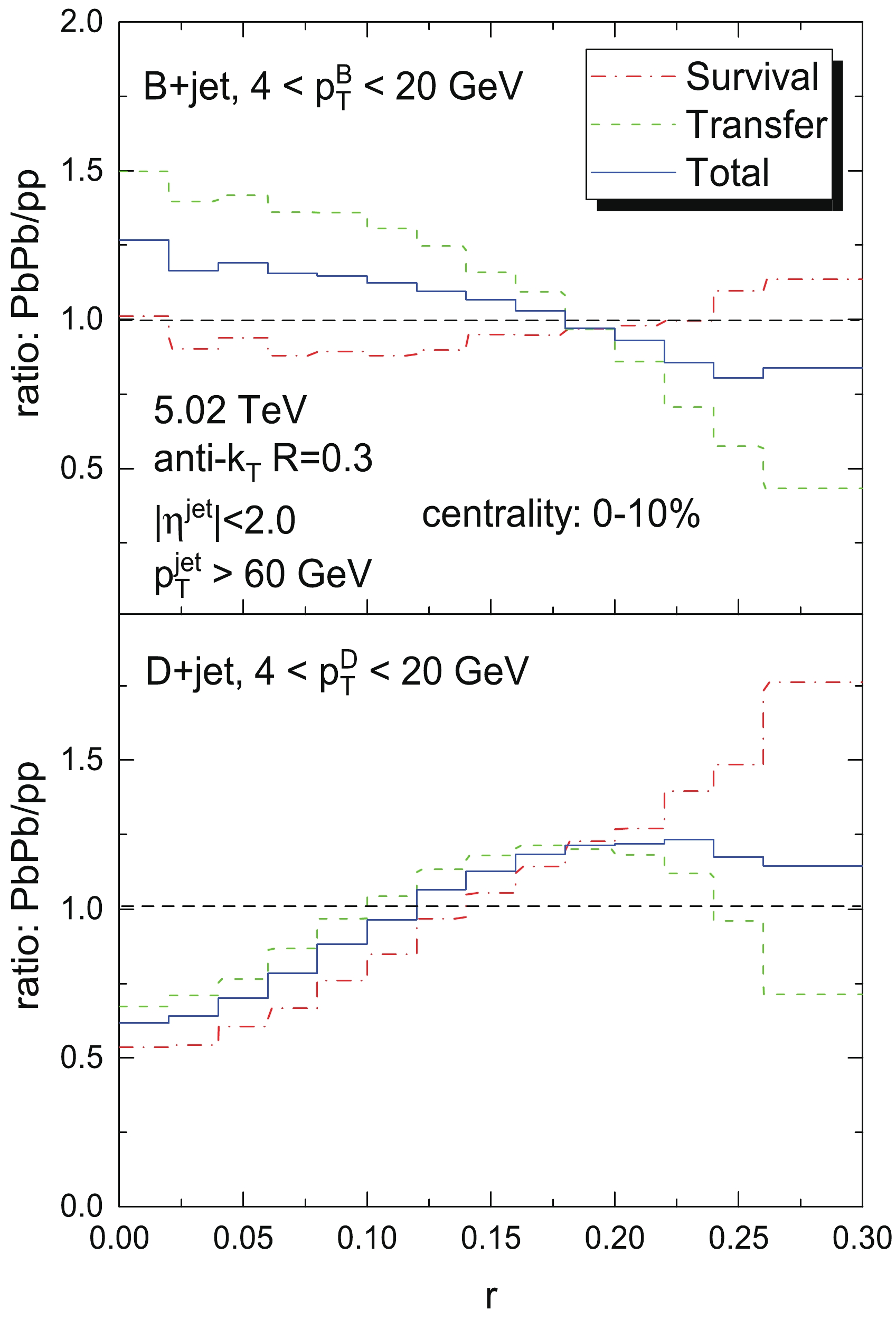
Figure 4. (color online) Medium modification patterns on the radial profiles of heavy flavor mesons (upper panel: B mesons, lower panel: D mesons) in jets from two kinds of contributions: Survival part (red dot-dashed line) and Transfer part (green dashed line), as well as the total contribution (blue solid line).
When we compare the modification patterns of B meson and D meson radial profiles in jets in the Survival and Transfer contributions respectively, we draw closer to revealing the nature of such inverse medium modification patterns. The comparison of the Survival modification pattern (dash dotted line) of B meson (top) and D meson (bottom) radial profiles in jets indicates that the same broader modifications of the radial distribution are shown in both the cases of B mesons and D mesons in jets due to the possible diffusion effects, as previously investigated in Ref. [74]. However, we observe a relatively smaller diffusion effect in the B meson radial profile in jets than in that of D mesons. For the case of the Transfer contribution, we find a narrower modification pattern of B meson radial profiles in jets but a broader modification pattern of D mesons in jets; the two opposite modification directions are mainly due to the competition of the two effects that lead to opposite consequences. One is that the Transfer part originally comes from a higher
$ p_T^Q $ trigger and is naturally distributed at smaller$ r $ ; when the ratio to the p+p baseline is taken, distribution shifting toward a narrower direction is observed. Meanwhile, the other fact is that the in-medium modification of such heavy flavor leads to a broader direction of distribution shifting due to the diffusion effect. These two effects offset each other. The former effect reveals the energy dissipation nature and the latter shows the diffusion feature that always leads to spreading away from the jet axis.From the discussion of Fig. 1, the
$ p_T^Q $ sensitivity of the initial radial distribution of B mesons in jets is larger than that of D mesons in jets, and it leads to a larger, narrower shifting toward smaller$ r $ of the radial distribution of B mesons in jets than that of D mesons in jets. Consequently, a larger, narrower shifting toward smaller$ r $ due to larger$ p_T^Q $ sensitivity of the initial radial distribution compared to charm quarks in jets and a smaller broader shifting towards smaller$ r $ due to its weaker diffusion effect compared to charm quarks in jets lead to an overall narrower shifting, which is exactly the opposite of the case of D mesons in jets.To further demonstrate that the angular diffusion effect of bottom quarks is much weaker compared to that of charm quarks in the medium, we first consider the impact of the interaction strength between charm and bottom quarks in QGP. We define
$ \Delta A = \sqrt{(\eta_Q-\eta_Q^0)^2+(\phi_Q-\phi_Q^0)^2} $

to quantify the angular deviation of the heavy quarks from their original moving directions during the in-medium propagation, where
$ \eta_Q^0 $ and$ \phi_Q^0 $ are the initial pseudorapidity and azimuthal angle of heavy quarks before entering the QGP medium. The angular deviation$ \Delta A $ directly represents the diffusion effect of the heavy quarks in the$ \eta-\phi $ plane due to collisional and radiative energy loss process in the QGP medium. In the top panel of Fig. 5, we calculate the angular deviation of charm and bottom quarks after the in medium modification as a function of their initial transverse momentum before energy loss in central Pb+Pb collision at$ \sqrt{s_{NN}} = $ 5.02 TeV. It is shown that diffusion strength decreases with the initial transverse momentum of heavy quarks, and the$ \Delta A $ of bottom quarks is smaller than that of charm quarks by nearly 20%-30%, as shown in the bottom panel of Fig. 5.
Figure 5. (color online) Angular deviation (
$ \Delta A $ ) of charm and bottom quarks relative to their initial moving direction in the medium as a function of transverse momentum, and the ratio of charm to bottom was shown at the lower panel.To explore further the distinction between the medium modifications of bottom quarks and charm quarks radial distributions in jets, we now consider the impact of the initial angular distance between the heavy quarks and the jet axis since they are quite different for the case of D mesons and B mesons in jets in the same
$ p_T^Q $ region in p+p. We plot in Fig. 6 the final observed angular shift$ \Delta r = r-r_0 $ of both D mesons and B mesons in jets in 0-10% Pb+Pb collisions at$ \sqrt{s_{NN}} = 5.02 $ TeV as functions of their initial angular distance with the jet axis$ r_0 $ . We find the angular shift of the charm quark is stronger than that of the bottom quark even at the same$ r_0 $ , and that the closer the heavy flavor quark is initially distributed away from the jet axis, the larger the final observed angular shift$ \Delta r $ will be. From the knowledge of Fig. 1, at the same$ p_T^Q $ trigger, the charm quark is always distributed closer to the jet axis than the bottom quark; therefore, it will eventually further enhance the difference in angular shift$ \Delta r $ between D mesons and B mesons in jets observed in the final-state.
Figure 6. (color online) Angular shift (
$ \Delta r = r-r_0 $ ) of charm and bottom quarks relative to the jet axis in the medium as a function of the initial angular distance to the jet axis ($ r_0 $ ).In the calculations
$ \hat{q} = q_0 (T/T_0)^3 $ is assumed, and we note that some possible non-perturbative non-conformal variations of$ \hat{q}(T,E) $ near the critical temperature$ T_{c} $ were suggested in recent studies [36,89]. It will be interesting to see how this non-conformal variation of$ \hat{q} $ influences the jet radial distribution in future studies, which may deepen our understanding of the QCD phase transition in the cross-over temperature range. -
In this work, we present a theoretical investigation of medium modifications of radial distributions of bottom quarks in jets in Pb+Pb collisions relative to those in p+p. We carry out the numerical calculations within a Monte Carlo simulation framework that utilizes the NLO+PS event generator SHERPA as input and use the SHELL model to take into account the in-medium jet energy loss for both heavy and light partons. In p+p collisions, we find that at lower
$ p_T^Q $ the radial profiles of heavy flavors in jets are sensitive to the heavy quark mass: bottom quarks trend to distribute in the region further from the jet axis due to their larger mass compared to that of charm quarks.Furthermore, to investigate the mass effect of heavy quarks reflected in the in-medium diffusion effect, we estimate the medium modification of the radial distribution of bottom quarks in jets, and we find an inverse modification pattern compared to that of charm quarks: jet quenching effects narrow the jet radial profile of bottom quarks while broadening that of charm quarks. By analyzing the event composition in Pb+Pb collisions, we find the main contribution of the event selected with
$ 4<p_T^Q<20 $ GeV in Pb+Pb collisions is dissipated from the higher$ p_T^Q $ region due to energy loss, namely the contribution of the Transfer part. We reveal that for both the cases of B mesons and D mesons in jets in A+A collisions, the Transfer part naturally has a narrower initial distribution and consequently leads to a narrower modification pattern of the radial profile; however, the diffusion nature of the heavy flavor in-medium interaction gives rise to a broader modification pattern of the radial profile. These two effects consequently compete with and offset each other. In the investigated$ p_T^Q $ region, we demonstrate that the b quarks in jets benefit more from the dissipation contribution from the higher$ p_T^Q $ region and suffers less diffusion effect compared to that of c quarks in jets. Hopefully, the sharp contrast of medium modification patterns between the radial profiles of charm and bottom mesons in jets at$ 4<p_T^{Q}<20 $ GeV predicted in this work can be tested against future experimental measurements at the LHC.The flavor dependence of jet quenching has been studied extensively and for a long time [27-45]; however, past studies of this kind have mainly focused on the magnitude difference of heavy quark energy loss due to the "dead-cone'' effect. In this paper, we demonstrate that the medium modifications of radial profiles of heavy quarks in jets are determined not only by how much the heavy quark loses its energy in the QGP but also more interestingly by the initial radial distributions of heavy quarks in jets, which exhibit quite distinct behaviors at different
$ p_T^Q $ kinematic cuts as shown in Fig. 1. Therefore, we observe that different initial distributions can ultimately lead to inverse medium modification patterns of B+jets and D+jets at$ 4<p_T^Q<20 $ GeV in Pb+Pb collisions. This reveals that, for some jet observables, the energy loss mechanism may not be the only factor in determining the final-state modification pattern in nucleus-nucleus collisions, and the initial differential distributions in p+p collisions may also play a very important role, which will then lead to much richer phenomena being observed in the flavor dependence of jet quenching in heavy-ion collisions.
Radial profile of bottom quarks in jets in high-energy nuclear collisions
- Received Date: 2021-01-24
- Available Online: 2021-06-15
Abstract: Angular correlations between a heavy quark (HQ) and its tagged jet are potentially new tools to gain insight into the in-medium partonic interactions in relativistic heavy-ion collisions. In this work, we present the first theoretical study on the radial profiles of B mesons in jets in Pb+Pb collisions at the Large Hadron Collider (LHC). The initial production of a bottom quark tagged jet in p+p is computed by SHERPA, which matches the next-to-leading order matrix elements with contributions of parton showers, whereas the massive quark traversing the quark-gluon plasma is described by a Monte Carlo model, SHELL, which can simultaneously simulate light and heavy flavor in-medium energy loss within the framework of Langevin evolution. In p+p collisions, we find that at lower





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: