Renormalizability of leading order covariant chiral nucleon-nucleon interaction

Since the pioneering works of Weinberg [1, 2], chiral effective field theory (ChEFT) has been successfully applied to describe the nucleon-nucleon interaction. Today, high precision chiral nuclear forces have become the de facto standard in ab initio nuclear structure and reaction studies [3-5]. Nevertheless, there are still a few outstanding issues in current research on chiral nuclear forces. One hotly discussed issue is their renormalizability; see, e.g., Refs. [6-9].

ChEFT is based on the chiral symmetry of QCD and its explicit and spontaneous breaking [10-15]. In ChEFT, the long-range interaction is provided by the exchange of the Goldstone bosons (pions in the u and d two-flavor sector and the pseudoscalar nonet in the u, d, and s three-flavor sector), and the short range interaction is described by the so-called low-energy constants (LECs) that encode the effects of degrees of freedom with energies larger than the chiral symmetry breaking scale, $ \Lambda_{\chi SB} $. In principle, these LECs can be calculated in the underlying theory, QCD, but in practice they can only be determined by fitting either to experimental or lattice QCD data, because of the non-perturbative nature of the low energy strong interaction. As a result, the predictive power of ChEFT relies on the fact that only a finite number of LECs contribute at a certain order and to a specific observable.

For an EFT, a proper power-counting (PC) scheme is the most important ingredient in order to perform any calculation. Current high precision chiral nuclear forces are based on the Weinberg PC (WPC) scheme, or the so-called naive dimensional analysis (NDA) [1, 2]. However, in the past two decades, there have been growing concerns that the WPC is inconsistent in the sense that the so-constructed chiral nuclear force is not renormalization group invariant (RGI), or, naively, is not cutoff-independent. The conventional way of examining RGI is to change the cutoff on a large scale and check whether the observables are cutoff-independent [16-19], since in any EFT, a separation (cutoff) between high- and low-energy physics should be offset with the LECs once one refits them for each new cutoff. However, there are other points of view on (non-perturbative) RGI. For instance, in Refs. [20-23] the authors argued that adopting a cutoff higher than a certain value (which normally ranges from $450 - 550$ MeV) will cause the “peratization” of an EFT and generate meaningless results. It has been suggested that the proper way to ensure RGI [24] is to examine whether the correction at a higher order i divided by the LO contribution, e.g., $\dfrac{\mathcal{O}_i(p)}{\mathcal{O}_{\rm LO}(p)}$, scales as $ \left(\dfrac{p,m_{\pi}}{M_{hi}}\right)^i $. In this work, we adopt the first approach. This means that the inconsistency problem already appears at leading order (LO) for the WPC [16, 17].

The pursuit of a consistent PC has continued for almost two decades. Using RGI as a guideline, it has been proposed that one can promote some of the higher-order terms in the WPC to make the chiral nuclear force renormalization group invariant at a specific order [25-28]. In principle, one can count how many counter-terms are needed before calculations are done by solving the Wilson RG-equation [29, 30]. A modified Weinberg approach with Lorentz-invariant contact interactions was proposed for nucleon-nucleon scattering in Ref. [31], and later applied to study hyperon-nucleon scattering in Ref. [32]. The modified Weinberg approach was further refined and applied to study baryon-baryon scattering [33, 34] with a different treatment of the one-pion (meson) exchange.

Recently, a covariant power-counting approach similar to the extended-on-mass-shell scheme in the one-baryon sector [35-37] was proposed for NN scattering [38], with the full structure of the Dirac spinor retained^①. It was shown that at LO the covariant approach can already provide a reasonably good description of the phase shifts of angular momentum $ J = 0 $ and 1 by solving the Kadyshevsky equation [39]. The numerical results remain almost the same if the Blankenbecler-Sugar [40] equation was used instead. This framework has then been successfully applied to study hyperon-nucleon interactions [41-44] and $ \Lambda_c N $ interactions [45]. In Ref. [46], it was shown that this formulation also provides a good description of the unique features of the $ ^1S_0 $ channel at leading order, in particular the pole position of the virtual bound state and the zero amplitude at the scattering momentum 340 MeV, which, according to Ref. [47], can serve as a nontrivial check on the self-consistency of any EFT for the nucleon-nucleon interaction.

From the perspective of the heavy baryon expansion, the covariant formulation can be viewed as an alternative power counting, which organizes the chiral expansion series differently. For instance, it includes all six allowed spin operators with four LECs at LO, while in the Weinberg approach they are only included up to NLO, which has 9 LECs. As such, a relatively faster convergence rate is achieved. This is understandable because one can show that the relativistic corrections in terms of $ q/(m_N c) $ are already comparable to the chiral corrections in terms of $ m_\pi/m_N $ for laboratory kinetic energies of 50 MeV.

Recently, the relativistic nucleon-nucleon two-pion-exchange (TPE) matrix elements have been constructed up to $ \mathcal{O}(q^3) $ [48]. It is shown that the contributions of relativistic TPE are more moderate than those of nonrelativistic TPE. They seem to converge faster than their nonrelativistic counterparts in almost all the partial waves studied in Ref. [48]. In particular, the relativistic corrections are found to play an important role in F-waves, especially the $ ^3F_2 $ partial wave.

As mentioned above, as a novel formulation of the chiral nuclear force, it is interesting to study whether the covariant power counting scheme can offer some new perspective on the issue of RGI. We note in passing that the community has not yet come to a consensus concerning expansions used to define “order” in non-perturbative systems (see, e.g., Refs. [9, 49]). Here, we follow Ref. [17] and define renormalization group invariance as the insensitivity of observables (phase shifts in the present work) to the cutoff used to regularize the potential, either relativistic or non-relativistic, up to a relatively large value, say, 10 GeV. The main purpose of the present work is to check whether the relativistic nuclear force is properly renormalized. It should be pointed out that the comparison is made to the Weinberg approach, not to the more recent refined versions, because the covariant approach is built upon the naive dimensional analysis of Weinberg. The results of the present study then can serve as further guidance to improve the covariant approach in the future.

This article is organized as follows. In Sec. II, we briefly introduce the covariant power counting (relativistic naive dimensional analysis) [50] and spell out the covariant nucleon-nucleon potential at leading order (LO). In Sec. III, we study the cutoff dependence of the partial wave phase shifts of $ J = 0 $ and 1, followed by a short summary in Sec. IV.

In this section, we briefly explain the relativistic naive dimensional analysis (NDA) (for more details see Ref. [50]) and spell out the LO partial wave potentials relevant to the present work.

To better understand the relativistic NDA, we first review the well-known Weinberg NDA. In the latter, the (non-relativistic) nucleon field is counted as of $ \mathcal{O}(q^0) $ and the gradient operators are of $ \mathcal{O}(q^1) $, where q denotes a typical soft scale, either the three-momentum of the nucleon or the light $ u/d $ quark mass, resulting in an expansion parameter $ q/\Lambda $ with $ \Lambda = m_N $ the nucleon mass or $ \Lambda_\mathrm{\chi SB} $ the chiral symmetry breaking scale. In the Weinberg NDA, the power counting is rather straightforward; one simply counts the number of gradient operators or the nucleon three-momentum.

In the relativistic NDA, the power counting is more involved. Because of the large nucleon mass in the chiral limit, a time-derivative acting on the nucleon field cannot be counted as of a small quantity. Inspired by the extended-on-mass-shell scheme in the one-baryon sector, one can instead count the nucleon field and the corresponding derivative in the following way:

where $ \partial_{\mu} $ is the derivative and $ \Psi $ is the nucleon field. The chiral dimensions of various Dirac matrices, the Levi-Civita tensor, and the derivative operators are listed in Table 1.

	1	$\gamma_{5}$	$\gamma_{\mu}$	$\gamma_{5}\gamma_{\mu}$	$\sigma_{\mu\nu}$	$\varepsilon_{\mu\nu\rho\sigma}$	$\overleftrightarrow{\partial_{\mu}}$	$\partial_{\mu}$
Chiral order	0	1	0	0	0	-	0	1

Table 1.  Chiral dimensions of Dirac matrices, the Levi-Civita tensor, and derivative operators. For the chiral counting of the various building blocks A, it should be understood that they operate either within or on a bilinear of the nucleon fields, i.e., $\bar{\Psi}A\Psi$ or $A\bar{\Psi}\Psi$ for $\partial_{\mu}$.

It should be noted that there are two derivatives. The derivative $ \partial_\mu $ acting on the whole bilinear is counted as of order $ \mathcal{O}(q^1) $, while the derivative $ \overleftrightarrow{\partial_\mu} $ acting inside a bilinear is counted as of $ \mathcal{O}(q^0) $ because of the large nucleon mass. The Levi-Civita tensor $ \epsilon_{\mu\nu\rho\sigma} $ contracting with n derivatives acting inside a bilinear raises the chiral order by $ n-1 $. If a derivative is contracted with one of the Dirac matrices $ \gamma_{5}\gamma_{\mu} $ or $ \sigma_{\mu\nu} $ in a different bilinear, the matrix element is of $ \mathcal{O}(q^1) $ [50].

One can easily check that by performing expansions in powers of $ 1/m_N $ the covariant Lagrangian can be reduced to the non-relativistic one. A careful examination of the expansion of the covariant Lagrangian shows clearly that in the covariant power counting the large scale is the nucleon mass (the chiral symmetry breaking scale) and the soft scale is the nucleon three-momentum, the same as in the Weinberg NDA. The only difference is that in the relativistic NDA, Lorentz covariance is fully satisfied by construction. i.e., by keeping the complete form of the Dirac spinor and using the building blocks of Table 1.

The LO nucleon-nucleon interaction contains five covariant four-fermion contact terms without derivatives and the one-pion-exchange (OPE) term [38],

The contact potential in momentum space reads

where $ C_{S,A,V,AV,T} $ are the LECs and $ u(\bar{u}) $ are the Dirac spinors,

with the Pauli spinor $ \chi_s $ and $ E_p $ (M) the nucleon energy (mass). According to Ref. [50], the $ C_A $ term should be counted as of $ \mathcal{O}(q^1) $. Nonetheless, this does not affect the present analysis in any significant way. As a result, to make easy comparison with Ref. [38], we keep the $ C_A $ term. The one-pion-exchange potential in momentum space is

where $ m_{\pi} $ is the pion mass, $ {{\mathit{\boldsymbol{p}}}} $ and $ {{\mathit{\boldsymbol{p'}}}} $ are initial and final three-momentum, $ g_{A} = 1.267 $, and $ f_{\pi} = 92.4 $ MeV. Note that the LO relativistic potentials already contain all six spin operators needed to describe nucleon-nucleon scattering.

The contact potentials can be projected into different partial waves in the $ |LSJ\rangle $ basis, which read:

where $ \xi_{N} = 4\pi N^2_{p}N^2_{p'}, R_{p} = |{{\mathit{\boldsymbol{p}}}}|/(E_{p}+ $$ M) $, $ R_{p'} = |{{\mathit{\boldsymbol{p'}}}}|/(E_{p'}+M) $, p and $ p' $ are the absolute values of $ {{\mathit{\boldsymbol{p}}}} $ and $ {{\mathit{\boldsymbol{p'}}}} $, and “$ \cdots $” denote higher order chiral terms in the WPC. Note that the expansions in $ 1/M $ shown for $ V_{1S0} $, $ V_{3S1} $, $ V_{3S1-3D1} $, and $ V_{3D1-3S1} $ are only done to guide the comparison with the Weinberg approach. In our study, we use the full potential without any approximations. The coefficients in the partial waves are linear combination of the LECs appearing in the Lagrangian,

We note that three of the eight partial wave coefficients are correlated, namely,

A few remarks are in order. First, it is clear that in the limit of $ M\rightarrow\infty $, only two LECs in the $ ^1S_0 $ and $ ^3S_1 $ channels remain, in agreement with the WPC. Second, the retaining of the full Dirac spinors in the Lagrangian not only leads to additional terms in the $ ^1S_0 $ and $ ^3S_1 $ partial waves (A large contribution of the correction terms is known to be essential to describe the $ ^1S_0 $ phase shifts [47, 51, 52]), but also provides contributions to other channels which are counted as of higher (than LO) order in the WPC. These new contributions will not only affect the description of the covariant nucleon-nucleon phase shifts but also the renormalizability of the chiral nuclear force. The latter is the main focus of the present work. Third, in the covariant PC, some of the LECs contribute to different partial waves, which is different from the WPC, where a LEC only contributes to a particular partial wave. It should be noted that the above correlations are only valid at LO, as can be explicitly checked using the higher order Lagrangians constructed in Ref. [50].

To take into account the non-perturbative nature of the nucleon-nucleon interaction, we solve the following Kadyshevsky equation with the kernel potential obtained above, $ V_\mathrm{LO}({{\mathit{\boldsymbol{p}}}}',{{\mathit{\boldsymbol{p}}}}) $:

To avoid ultraviolet divergence, we need to introduce a regulator $ f(p,p') $. In principle, physical observables should be independent of the choice of regulator if the EFT is properly formulated, i.e., if the EFT is RGI. Here we choose the commonly used separable cutoff function in momentum space, $ f(p,p') = \rm{exp}\Bigg[\dfrac{-{{\mathit{\boldsymbol{p}}}}^{2n}-{{\mathit{\boldsymbol{p}}}}'^{2n}}{\Lambda^{2n}}\Bigg] $, with $ n = 2 $. The convenience of such a regulator lies in that it only depends on initial and final momenta, so it does not interfere with partial wave decomposition.

In this section, we present the fitting strategy and results of the RG-analysis for all the $J = 0,1$ partial waves.

Numerically, we fit the Nijmegen partial wave phase shifts of the np channel [53]. At LO, there are five linear independent LECs and they can be divided into three groups according to Eq. (14): 1) $ C_{3P0} $; 2) $ C_{1S0},\hat{C}_{1S0},C_{3P1} $; and 3) $ C_{3S1},\hat{C}_{3S1},C_{1P1} $. In groups 2 and 3, only two of the three LECs are linear independent.

Since our aim is to study the dependence of observables, here phase shifts, on the chosen value of the cutoff, we fit the coefficients of the partial wave potentials rather than the LECs of the Lagrangian. First, we fit $ C_{3P0} $ to the $ ^3P_{0} $ phase shift at $ T_\mathrm{lab.} = 10 $ MeV. Then we fit $ C_{3P1} $ and $ C_{1S0} $ to the two $ ^1S_{0} $ phase shifts at $ T_\mathrm{lab.} = 10 $ and 25 MeV. Last, we fit $ C_{1P1} $ and $ C_{3S1} $ to the $ ^1P_{1} $ and $ ^3S_{1} $ phase shifts at $ T_\mathrm{lab.} = 10 $ MeV. In the fitting, we take into account that $ \hat{C}_{1S0} = C_{1S0}-C_{3P1} $ and $ \hat{C}_{3S1} = 3C_{3S1}-3C_{1P1} $.

The reason we adopt such a fitting strategy is that $ ^3P_{1} $ is not renormalization group invariant with a potential of the form $V_{3P1} = {\rm OPE}+C_{3P1}pp'$, as already shown in Ref. [54]. Therefore, we should use the two $ ^1S_{0} $ LECs to predict the $ ^3P_{1} $ phase shifts, since they are coupled in the covariant PC scheme. More discussion is given in Sec. III D.

In the fitting, we define a chi-squared-like function $ \tilde{\chi}^2 $ as $ \tilde{\chi}^2 = (\delta_{ \rm{LO}}-\delta_{ \rm{PWA}})^2 $. That is, we neglect the uncertainties in the data, as they are much smaller than the higher chiral order contributions. In our study the momentum cutoff $ \Lambda $ is varied from 0.4 GeV to 10 GeV, except for the $ ^1S_{0} $ and $ ^3P_{1} $ channels, due to the reasons explained below.

It is instructive to compare the covariant framework with the non-relativistic one, on which the Weinberg counting is based, when only the long-range force — OPE — is present. The phase shifts for different laboratory energies as a function of the cutoff are shown in Fig. 1. It is clear that the OPE is cutoff-independent for the $ ^1P_1 $ and $ ^3P_1 $ channels, while it is not for the $ ^3P_0 $ channel, where a limit-cycle-like behavior appears in both approaches. However, as already noticed in Ref. [32], the interval between adjacent cycles is bigger in the Kadyshevsky equation (used in the covariant scheme) than in the Lippmann-Schwinger approach (used in the Weinberg approach). In the present case, the second cycle appears at $ \Lambda = 10.6 $ GeV in the covariant scheme.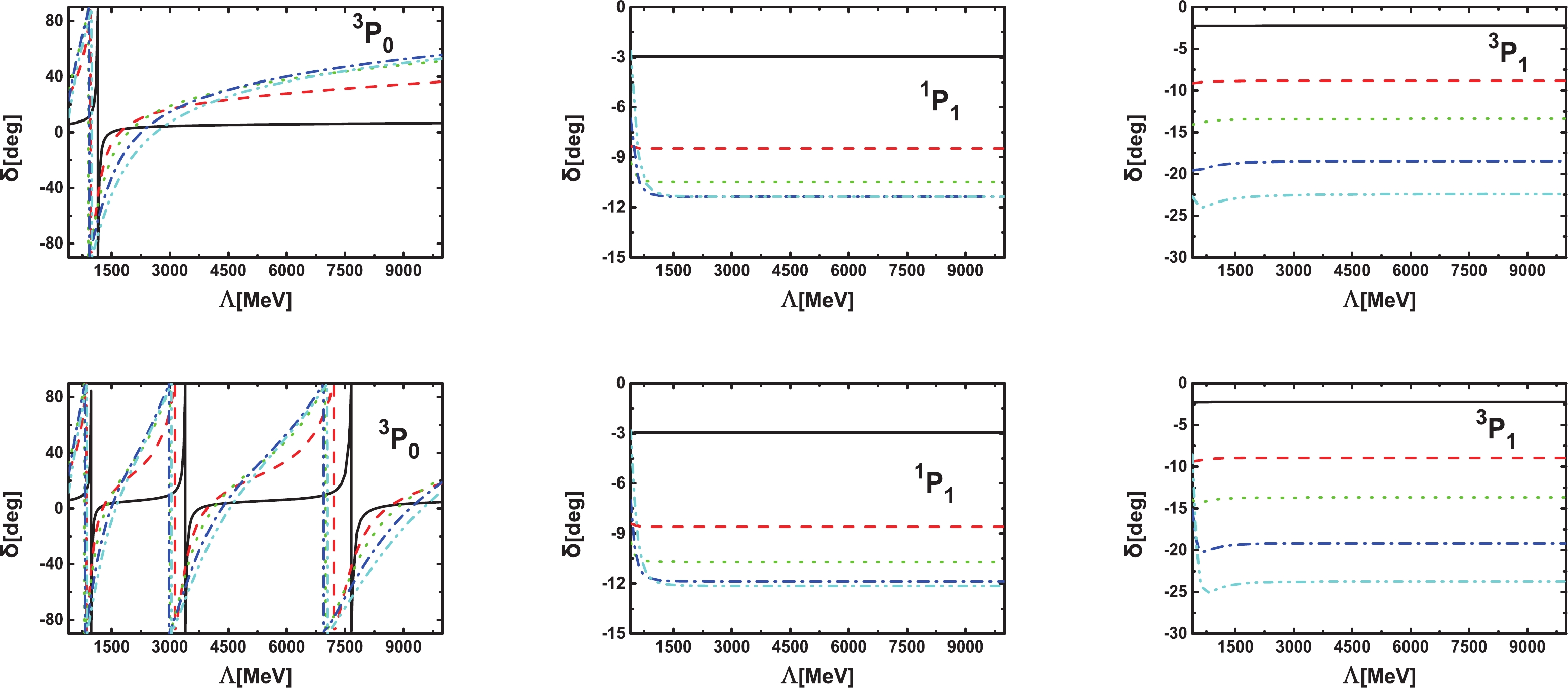

Figure 1.  (color online) Comparison of the $ ^3P_{0} $, $ ^1P_{1} $, and $ ^3P_{1} $ phase shifts (as functions of the $ \Lambda $) for laboratory energies of 10 MeV (black solid lines), 50 MeV (red dashed lines), 100 MeV (green dotted lines), 190 MeV (blue dash-dotted lines), and 300 MeV (cyan dash-dot-dotted lines). Phase shifts in the upper row are obtained in the covariant scheme, while those in the lower row are obtained in the Weinberg scheme. Note that only the OPE contribution is considered.

We note in passing that although the OPE for $ ^3P_1 $ is cutoff-independent, once a contact term is added and fixed by fitting to the corresponding phase shift, this channel becomes cutoff-dependent, both in the present case and in Ref. [54].

We first study the much discussed $ ^3P_0 $ channel, where in the Weinberg scheme RGI is lost. In our covariant scheme, the $ ^3P_{0} $ channel is not coupled to any other channel and the corresponding contact potential is given in Eq. (13). The phase shifts as functions of $ \Lambda $ and laboratory energies are shown in Fig. 2. From the left-hand panel, one finds that the dependence on $ \Lambda $ becomes weaker and weaker with increasing $ \Lambda $, even for $ T_\mathrm{lab.} $ up to 300 MeV. From the perspective of RGI, the covariant PC is consistent for this channel. From the right-hand panel, one can see that the agreement between theory and experiment is very good up to $ T_\mathrm{lab.} = 200 $ MeV. One should note that in Ref. [31], such a term was promoted to LO in order to achieve RGI for this channel.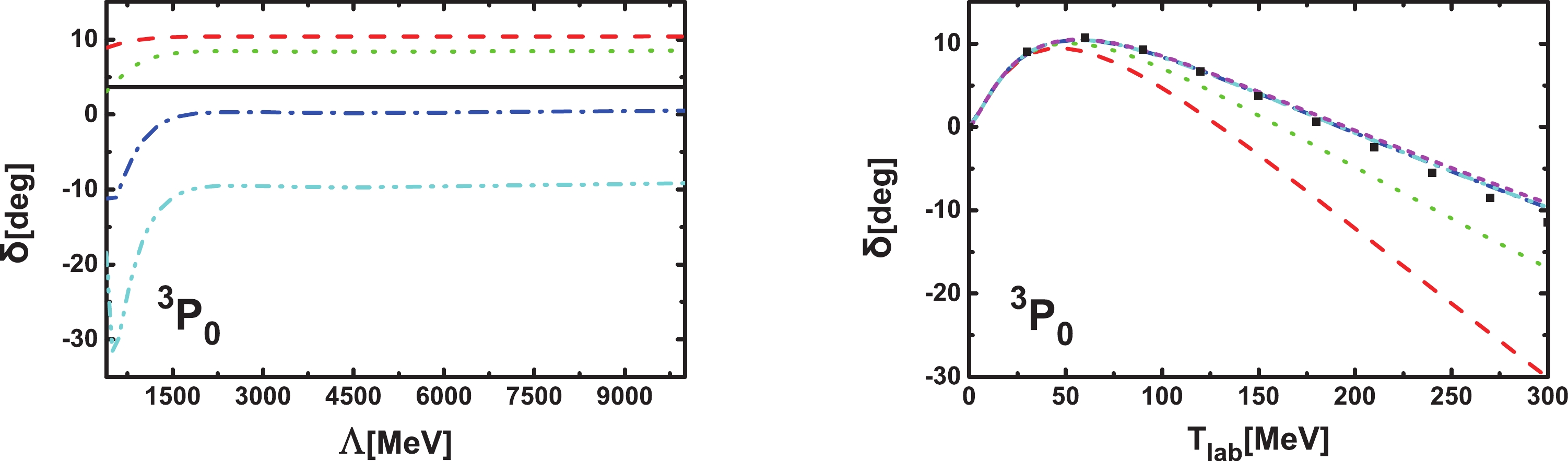

Figure 2.  (color online) Phase shifts as functions of the cutoff $ \Lambda $ for laboratory energies of 10 MeV (black solid line), 50 MeV (red dashed line), 100 MeV (green dotted line), 190 MeV (blue dash-dotted line), and 300 MeV (cyan dash-dot-dotted line), and as functions of laboratory energies with $ \Lambda = 600 $ MeV (red dashed line), 1000 MeV (green dotted line), 2000 MeV (blue dash-dotted line), 5000 MeV (cyan dash-dot-dotted line), and 10000 MeV (magenta short dashed line). The black diamonds denote the Nijmegen phase shifts [53].

In the non-relativistic pion-less EFT, it has been shown that the Wigner bound [55] strongly constrains the effective range for large cutoffs [56, 57]. We have observed numerically a similar bound in the $ ^1S_{0} $ channel with the covariant integral equation (15): for cutoff values larger than $ \sim 650 $ MeV, the $ ^1S_{0} $ scattering length and effective range cannot simultaneously be fitted to their empirical values. Regarding the previously stated fitting strategy, this means that, for large enough cutoff values, we can no longer make predictions for $ ^3P_{1} $ from the $ ^1S_{0} $ inputs. With $ C_{3P1} $ fitted to the $ ^3P_{1} $ phase shifts, RGI is lost because OPE is singularly repulsive for this partial wave [54]. We note that one possible solution has been suggested in two recent works: perturbation theory for all the partial waves except for $ ^1S_0 $, $ ^3S_1 $-$ ^3D_1 $, and $ ^3P_0 $ [58, 59].

It is still worth studying these softer cutoffs, so in the following we focus on the region of $ \Lambda = 400 - 650 $ MeV. From Eq. (5), it is clear that the nominally higher order contributions can simulate the finite-range nature of the $ ^1S_0 $ potential. With two LECs, we can reproduce the scattering length and effective range simultaneously. This implies that one can describe the corresponding phase shifts better than the LO Weinberg approach, as verified numerically in Ref. [46]. The phase shifts as functions of the cutoff $ \Lambda $ for $ ^1S_{0} $ and $ ^3P_{1} $ are shown in Fig. 3. One can see that the dependence on the cutoff in the limited cutoff region is rather weak for both $ ^1S_0 $ and $ ^3P_1 $, keeping in mind that the latter is predicted using $ C_{3P1} = C_{1S0}-\hat{C}_{1S0} $. In Fig. 4, we see that as the cutoff increases from 450 to 650 MeV, the descriptions of the two phase shifts become better.

Figure 3.  (color online) Cutoff dependence of the $ ^1S_0 $ and $ ^3P_1 $ phase shifts for laboratory energies of 10 MeV (black solid lines), 25 MeV (red dashed lines), 50 MeV (green dotted lines), 100 MeV (blue dash-dotted lines), 190 MeV (cyan dash-dot-dotted lines), and 300 MeV (magenta short dashed lines).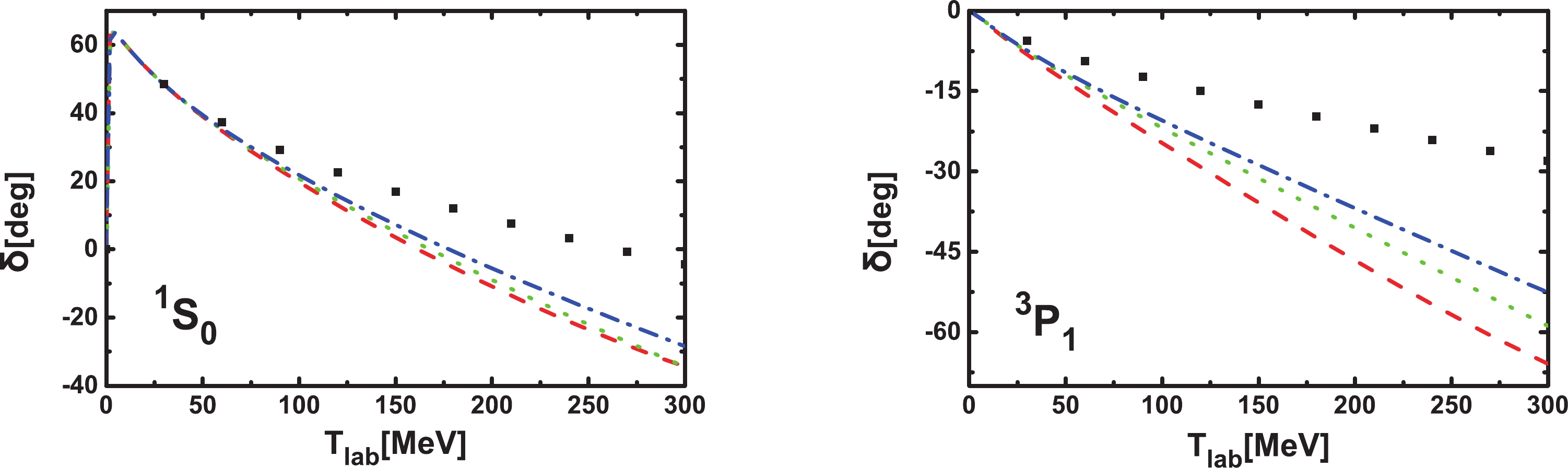

Figure 4.  (color online) Comparison of the $ ^1S_0 $ and $ ^3P_1 $ phase shifts (as functions of the laboratory energy) with $ \Lambda = 450 $ MeV (red dashed lines), 550 MeV (green dotted lines), and 650 MeV (blue dash-dotted lines) with the Nijmegen phase shifts (black diamonds) [53].

The $ ^3S_{1} $, $ ^3D_{1} $, $ E_{1} $, and $ ^1P_{1} $ phase shifts as functions of $ \Lambda $ are shown in Fig. 5. It is clear that the dependence on $ \Lambda $ becomes weaker for larger $ \Lambda $, indicating that for all these channels RGI is satisfied.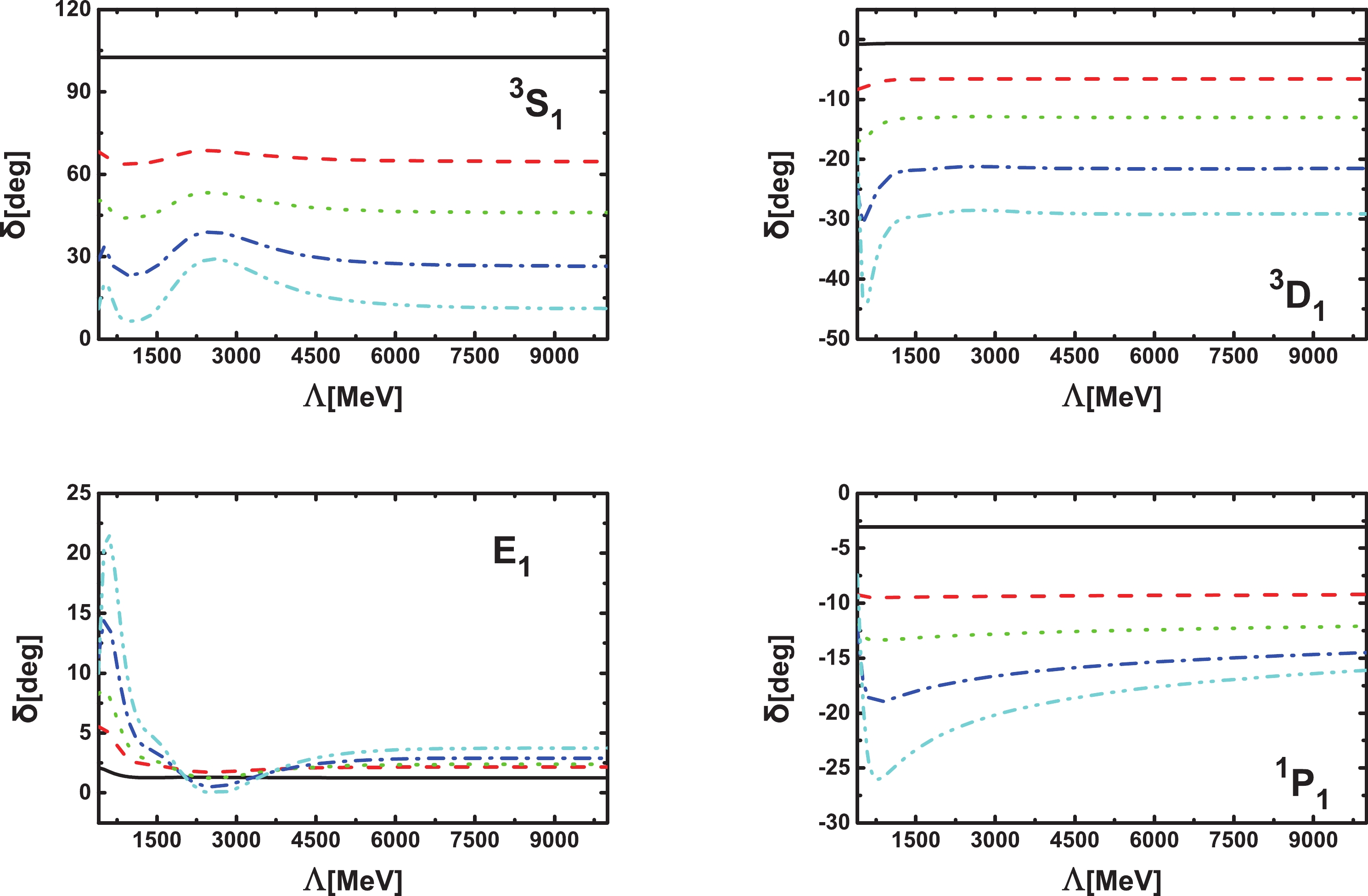

Figure 5.  (color online) The $ ^3S_{1} $, $ ^3D_{1} $, $ E_{1} $, and $ ^1P_{1} $ phase shifts for laboratory energies of 10 MeV (black solid lines), 50 MeV (red dashed lines), 100 MeV (green dotted lines), 190 MeV (blue dash-dotted line), and 300 MeV (cyan dash-dot-dotted lines) as functions of the cutoff $ \Lambda $.

The phase shifts of these four channels are compared with those of the Nijmegen phase shifts in Fig. 6. For $ ^3S_{1} $, the agreement is fairly good when the phase shifts converge. For $ ^1P_{1} $, the agreement is good below $ T_\mathrm{lab.} = 70 $ MeV. As the cutoff increases, the deviation becomes larger for high laboratory energies and therefore higher chiral order contributions are needed. For $ E_{1} $, the agreement with the Nijmegen analysis is quite good even up to $ T_\mathrm{lab.} = 300 $ MeV when it converges. For $ ^3D_{1} $, the agreement is good up to $ T_\mathrm{lab.}<100 \rm{MeV} $.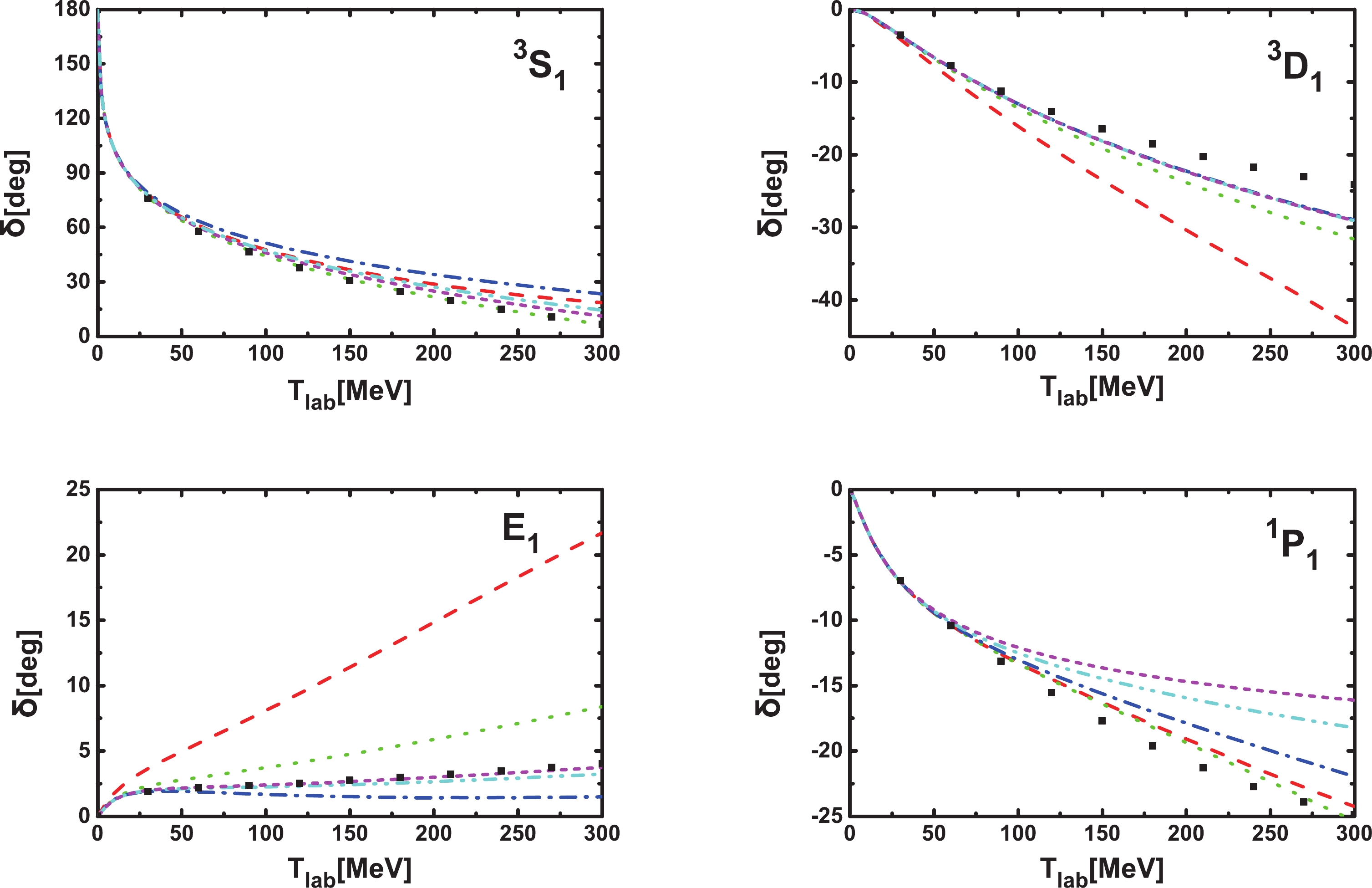

Figure 6.  (color online) Comparison of the $ ^3S_{1} $, $ ^3D_{1} $, $ E_{1} $, and $ ^1P_{1} $ phase shifts (as functions of the laboratory energy) with $ \Lambda = 600 $ MeV (red dashed lines), 1000 MeV (green dotted lines), 2000 MeV (blue dash-dotted lines), 5000 MeV (cyan dash-dot-dotted lines), and 10000 MeV (magenta short dashed lines) with the Nijmegen phase shifts (black diamonds) [53].

In this work, we have analyzed the renormalization group invariance of the LO covariant chiral nucleon-nucleon force. There are five LECs for all the $ J = 0,1 $ channels. We identified the relations among them and checked the consistency of power counting from the perspective of renormalization group invariance for the $ ^3S_{1} $, $ ^3D_{1} $, $ E_{1} $, $ ^3P_{0} $, and $ ^1P_{1} $ channels. For the much-discussed $ ^3P_0 $ channel, renormalization group invariance is automatically satisfied in the covariant power counting. On the other hand, the $ ^1S_{0} $ and $ ^3P_{1} $ channels are correlated. Therefore, we fixed the LECs $ C_{1S0} $ and $ \hat{C}_{1S0} $ by fitting to the $ ^1 S_0 $ phase shifts and used the relation $ \hat{C}_{1S0} = C_{1S0}-C_{3P1} $ to predict $ C_{3P1} $. Since the Wigner bound restricts the maximum cutoff allowed for this channel, we only varied the cutoff in a limited region of 400-650 MeV. The resulting phase shifts for the two channels are reasonable. Similar to the Weinberg power counting, the $ ^3S_{1} $, $ ^3D_{1} $, $ E_{1} $ and $ ^1P_{1} $ channels are renormalization group invariant.

It must be noted that after many years of extensive studies, there is not yet a consensus on the meaning of, and no universally accepted solutions to, the non-perturbative renormalization of the pion-ful chiral nuclear force. The present work should only be viewed as a new attempt at tackling this long-standing problem from a different perspective. The results shown in the present work indicate that we are still far away from providing a solution and therefore more work is needed, such as a detailed study along the same lines at higher chiral orders.

CXW thanks Xiu-Lei Ren for useful discussions in the early stage of the present work. We would like to thank Manuel Pavon Valderrama and Bira van Kolck for stimulating discussions and comments on various occasions.

In Fig. A1, we show the $ ^3P_1 $ phase shifts with the LEC $ C_{3P1} $ fixed by fitting to the phase shift at 50 MeV. It is clear that renormalization group invariance is not achieved for the $ ^3P_1 $ channel. This conclusion is similar to that of Ref. [18], where it was shown that contact interactions for the $ ^3P_1 $ channel, if treated non-perturbatively, destroy the renormalizability of this channel .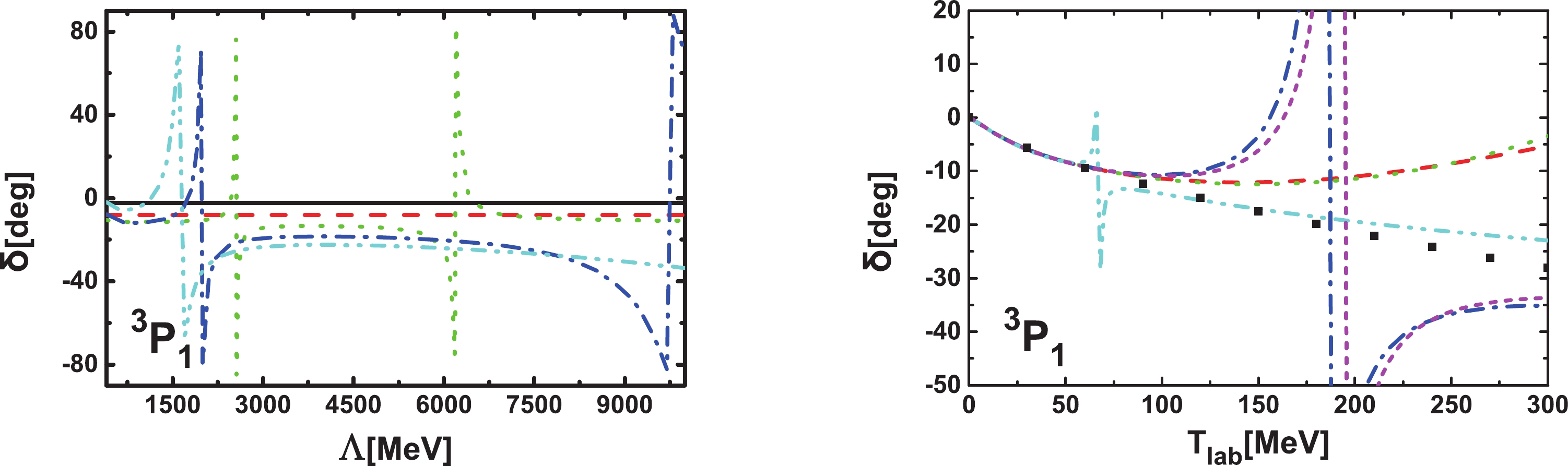

Figure A1.  (color online) Phase shifts as functions of $ \Lambda $ for laboratory energy of 10 MeV (black solid line), 50 MeV (red dashed line), 100 MeV (green dotted line), 190 MeV (blue dash-dotted line), 300 MeV (cyan dash-dot-dotted line) and as functions of laboratory energies with $ \Lambda $ fixed at 600 MeV (red dashed line), 1000 MeV (green dotted line), 2000 MeV (blue dash-dotted line), 5000 MeV (cyan dash-dot-dotted line), and 10000 MeV (magenta short dashed line). The black diamonds denote the Nijmegen phase shifts [53].