-
Synthesis of heavy and superheavy nuclei using the fusion evaporation reaction [1-3] and multinucleon transfer reaction [4, 5] is one of the major aims of low-energy heavy-ion physics. Theoretically, the evaporation residue cross section (ERCS) of heavy and superheavy nuclei can be divided into the product of three factors [6-8]. One of the critical factors is the survival probability of the compound nucleus against fission in the deexcitation process [9-15]. In addition, the deexcitation process of primary fragments produced by multinucleon transfer is directly related to the survival probability [16, 17].
To describe the deexcitation process of an excited compound nucleus, two common approaches are used to describe the fission process, namely the dynamical [18-20] and statistical [21-25] approaches. In addition, both approaches need to consider the change in the nuclear structure (shell structure) with the excitation energy. In this article, statistical models are used, and two different ways of considering the influence of shell effect washout with the excitation energy on the survival probability are analyzed. One approach involves the modification of the Fermi-gas level density parameter suggested by Ignatyuk [26].
Another approach assumes the smearing of microscopic shell effects with excitation energy in the nuclear binding energies (effective compound nucleus ground state) and the potential energy surface [19, 20]. If the ground state of the binding energies and potential energy surface is converted into an effective potential energy surface, the influence of the excitation energy on the shell effect can be introduced in the microscopic part of the macroscopic-microscopic model. Moreover, to consider the self-consistency caused by the change in the zero-potential energy reference point, we need to calculate the neutron separation energy based on the nuclear binding energy containing temperature effects.
The uncertainty of survival probability calculated based on statistical models mainly comes from two aspects. On the one hand, the survival probabilities of
$ xn $ neutron evaporation channels is particularly sensitive to the model input or related parameters [10, 27-30]. For example, the level density parameters, fission barriers and neutron separation energies, and transmission coefficients should be known to be accurately sufficient. In contrast, many approximations are involved when calculating the survival probability [18-21, 24, 25]. Thus, a reaction system with a sufficiently large number of projectile-target combinations should be considered within the same set of parameters and assumptions. In addition, by comparing the theoretical calculations with the available experimental data, one can clearly see whether the parameters are reasonable.In the present work, we calculated the evaporation residual cross section of some superasymmetric reaction systems. In addition, as all the projectile-target combinations selected in the considered reactions have relatively higher asymmetry, we can therefore assume the absence of a dynamics hindrance factor in the process of fusion, i.e,
$ P_{\rm CN} \approx1 $ . In addition, if the theoretical calculation of the capture cross section is in good agreement with the experimental data, then this unique set of experimental data will impose sufficiently strong constraints to unambiguously verify the basic assumptions underlying the calculations of the survival probabilities. -
The ERCS of the compound nucleus can be defined as follows [6-8]:
$ \begin{split} \sigma_{\rm{ERCS}}(E_{\rm{c.m.}}) =& \sum\limits_{J = 0}^{J_{\rm{max}}} \sigma_{\rm{capture}}\left(E_{\rm{c.m.}}, J\right) \\ &\times P_{\rm{CN}}\left(E^{*}_{\rm CN}, J\right) W_{\rm{sur}}\left(E^{*}_{\rm CN}, J\right), \end{split}$

(1) where
$ \sigma_{\rm{ERCS}} $ is the product of the capture cross section$ \sigma_{\rm cap} $ , fusion probability$ P_{\rm{CN}} $ , and survival probability$ W_{\rm{sur}} $ , and$ E_{\rm c.m.} $ is the incident energy in the center of mass system.$ E_{\rm{CN}}^{*} $ and J separately represent the excitation energy and spin angular momentum of the compound nucleus, where$ E_{\rm{CN}}^{*} = E_{\rm{c.m.}}+Q $ ,$ Q = M(P) c^{2}+ M(T) c^{2}- M(C) c^{2} $ ,$ M(P) $ ,$ M(T) $ , and$ M(C) $ represent the mass of the projectile nucleus, target nucleus, and compound nucleus, respectively.The capture cross section
$ \sigma_{\rm cap}(E_{\rm c.m.},J) $ in Eq. (1) is determined by the penetration probability$ T\left(E_{\rm c . m .}, J\right) $ of the two colliding systems overcoming the Coulomb potential barrier in the entrance channel to form the DNS. The corresponding expression is defined as [31]:$ \begin{split} \sigma_{\rm cap}(E_{\rm c.m.},J) =& \frac{\pi\hbar^{2}}{2\mu E _{\rm c.m.}}\int_{0}^{\pi/2}\sin\theta_{1}{\rm d}\theta_{1}\\ &\times\int_{0}^{\pi/2}(2J+1)T(E_{\rm c.m.},J,\theta_{1},\theta_{2})\sin\theta_{2}{\rm d}\theta_{2}, \end{split}$

(2) where
$ T(E_{\rm c.m.},J,\theta_{1},\theta_{2}) $ denotes the transmission probability, which can be expressed as [32, 33]$ \begin{split} T(E_{\rm c.m.},J, \theta_{1},\theta_{2}) = \frac{1}{1+\exp\left\{-\dfrac{2\pi}{\hbar\omega(J)}\left[E_{\rm c.m.}-B(\theta_{1},\theta_{2})-\dfrac{\hbar^{2}}{2\mu R_{B}^{2}}J(J+1)\right]\right\}}, \end{split}$

(3) where
$ \hbar\omega(J) $ is the width of the parabolic Coulomb barrier at position$ R_{B}(J) $ , and$ B(\theta_{1},\theta_{2}) $ is the orientation dependent barrier.The
$ P_{\rm{CN}}\left(E^{*}, J\right) $ term in Eq. (1) is the probability that the dinuclear system evolves from a touching configuration to form a compound nucleus [6]. Furthermore, the fusion probability$ P_{\rm{CN}}\left(E^{*}, J\right) $ depends on the competition between the complete fusion and quasifission process. However, there is almost no effect of the dynamical fusion hindrance on the collision of superasymmetric reaction systems. Our calculations assume that the fusion probability$ P_{\rm CN}\approx1 $ . However, if the asymmetry decreases and tends to a symmetrical system, then the quasifission channel will become increasingly important, i.e.,$ P_{\rm CN}<1 $ .The
$ W_{\rm{sur}}\left(E^{*}, J\right) $ term in Eq. (1) represents the survival probability of the excited compound nucleus with a certain excitation energy$ E^{\ast} $ and angular momentum J [7]. Furthermore, the survival probabilities of excited compound nuclei in the process of deexcitation via neutron evaporation,$ \gamma $ -ray emission, and light particle evaporation in competition with fission can be estimated within the statistical evaporation model. The most noteworthy point is that the excited compound nuclei are generally considered to be cooled mainly by neutron evaporation and fission in the medium excitation energy range ($ E^{*}_{\rm CN} = 10-60 $ MeV).The survival probability of neutron deficient compound nuclei is an interesting research topic because many fusion reactions of heavy nuclei lead to the formation of a neutron-deficient compound nucleus. In addition, the production of heavy [34-36] and superheavy nuclei [37-39] in fusion reactions accompanied by the evaporation of charged particles has been discussed previously in theoretical and experimental studies. Furthermore, there is experimental evidence that the evaporation of charged particles in the deexcitation of neutron deficient compound nuclei successfully competes with neutron emission [7]. In fact, it is necessary to take into consideration the evaporation channels of charged particles when calculating the survival probability at high excitation energies. We will study these effects in further studies.
The survival probability of vaporizing
$ xn $ neutrons can be expressed as:$ W_{\rm{sur}}\left(E_{\rm{c.m.}}\right) \approx P_{x n}\left(E_{\rm{CN}}^{*}\right) \prod\limits_{i = 1}^{x} \frac{\Gamma_{n}\left(E_{i}^{*}\right)}{\Gamma_{n}\left(E_{i}^{*}\right)+\Gamma_{\rm f}\left(E_{i}^{*}\right)}, $

(4) where
$ P_{xn} $ is the probability of vaporizing$ xn $ neutrons at a given excitation energy$ E_{\rm{CN}}^{*} $ [40].$ \Gamma_{n} $ and$ \Gamma_{\rm f} $ are the neutron evaporation width and fission width, respectively.$ E_{i}^{*} $ is the compound nuclear excitation energy before vaporization of the$ i $ th neutron.The partial width for the emission of a neutron from a compound nucleus with the excitation energy
$ E_0 $ is given by the Weisskopf formula [41]$ \Gamma_{n} = \frac{gm_{n}\sigma_{\rm inv}}{\pi^2\hbar^2\rho_{0}(E_0-\delta_0)}\int_{0}^{E_0-B_n-\delta_n}\rho_{n}(E_0-B_n-\delta_n-\varepsilon)\varepsilon {\rm d}\varepsilon, $

(5) where
$ m_{n} $ and g are the mass and spin degeneracy of the emitted neutron, and$ \sigma_{\rm inv} $ is the cross section of the decaying nucleus formed in the inverse process. The$ \rho_{0}(E_{0}-\delta_0) $ term is the level density of the parent nucleus at the thermal excitation energy of its corrected pairing energy$ \delta_0 $ , and$ \rho_{n}(E_0-B_n-\delta_n-\varepsilon) $ is the corresponding level density of the daughter nucleus after emitting a neutron.$ B_n $ is the neutron separation energy, and$ \delta_n $ is the pairing energy of the daughter nucleus.The fission width can be expressed in terms of the transition state theory as [18]
$ \Gamma_{\rm f}^{\rm BW} = \frac{1}{2\pi\rho_{0}(E_0-\delta_0)}\int_{0}^{E_0-B_{\rm f}-\delta_{\rm f}}\rho_{\rm f}(E_0-B_{\rm f}-\delta_{\rm f}-\varepsilon) {\rm d}\varepsilon, $

(6) where
$ \rho_{\rm f}(E_0-B_{\rm f}-\delta_{\rm f}-\varepsilon) $ is the level density of the fissile nucleus at the saddle configuration.The back-shift Fermi-gas model is used to determine the level density [42],
$\begin{split} \rho(U,J) = \frac{(2J+1)\exp{\left[2\sqrt{aU}-\frac{J(J+1)}{2\sigma^2}}\right]}{24\sqrt{2}\sigma^3 a^{1/4} U^{5/4}}, \end{split} $

(7) where
$ \sigma^2 = \dfrac{\Theta_{\rm rigid}}{\hbar^2}\sqrt{\frac{U}{a}} $ ,$ \Theta_{\rm rigid} = \dfrac{2}{5}m_{u}AR^2 $ , and$ U = E-\delta_0 $ . The back shifts$ \delta = -\Delta $ (odd-odd), 0 (odd A), and$ \Delta $ (even-even), respectively, are related to the neutron and proton pairing gap$ \Delta = 1/2[\Delta_n(Z,N)+\Delta_p(Z,N)] $ obtained from the mass differences of the neighboring nuclei.One way to consider that the washing out of shell effects with increasing excitation energy is introduced in the nuclear level density parameter is by proposing an exponential function. The dependence of the level density parameter a on the shell correction and excitation energy was initially proposed as
$ a(U,Z,N) = \tilde{a}(A)\left[1+\delta W_{\rm shell}\frac{f(U)}{U}\right] $

(8) with
$ \tilde{a}(A) = \alpha A+\beta A^{2/3} $ and$ f(U) = 1-\exp{(-\gamma_D U)} $ . The values of the free parameters$ \alpha $ ,$ \beta $ , and$ \gamma $ are determined by fitting to the experimental level density data [42]. The fission barrier$ B_{\rm f} = B_{\rm f}^{\rm L D}+B_{\rm f}^{\rm M}(E^{*} = 0) $ remains constant.The fission barrier height
$ B_{\rm f} $ in Eq. (6) consists of the liquid drop$ B_{\rm{f}}^{\rm L D} $ and microscopic$ B_{\rm f}^{\rm M} $ parts in the macroscopic-microscopic approach. The liquid drop part was calculated according to the angular momentum dependent macroscopic fission barriers described by the finite range liquid model [43]. The microscopic value$ B_{\rm f}^{\rm M} = \delta W_{\rm shell}^{\rm saddle}-\delta W_{\rm shell}^{\rm{\rm gs}} $ is the difference between the shell correction energy of the saddle point and shell correction energy of the ground state [44]. In addition, the systematics analysis shows that the values of$ \delta W_{\rm shell}^{\rm saddle} $ are close to zero for the nuclei with$ 80\leqslant Z\leqslant 100 $ [24]. Therefore, the present theoretical calculations can be used to experimentally determine the measured values of the fission barrier when we assume the shell correction energy of the saddle point as$ \delta W_{\rm shell}^{\rm saddle} = 0 $ [24].Another way to consider the washing out of shell effects with increasing excitation energy is to focus on the dependence of the fission barrier on the excitation energy. This energy dependence can be attributed to an effective compound nucleus ground state, where the ground state shell correction is washed out by the excitation energy. Therefore, the dependence of the fission barrier on the excitation energy is given by the following formula:
$ B_{\rm f}\left(E_{\rm C N}^{*}\right) = B_{\rm f}^{\rm L D}+B_{\rm f}^{\rm M}\left(E_{\rm C N}^{*} = 0\right) \exp \left[-E_{\rm C N}^{*} / E_{\rm D}\right] $

(9) $ E_{\rm D} $ is the shell damping factor that describes the decrease in the shell effect with increase in the nuclear excitation energy.From a theoretical point of view, the washing out of microscopic effects with the excitation energy in the level density should be equivalent to smearing microscopic effects on the effective potential energy surface [28]. To ensure self-consistency in the calculation, we need to calculate the neutron separation energy through the effective compound nucleus ground state. For FRDM1995 [44], the dependence of the nuclear binding energies on the excitation energy can be expressed as
$ E(N,Z) = E_{\rm mac}(N,Z)+E_{\rm mic}\exp \left[-E_{\rm C N}^{*} / E_{\rm D}\right], $

(10) where usually
$ E_{\rm mic} $ is tabulated, and$ E_{\rm D} $ is the effective shell damping energy. -
Figure 1 shows the capture cross section
$ \sigma_{\rm cap} $ as a function of the excitation energy$ E^{*}_{\rm CN} $ . In addition, we compared the theoretical calculations of the capture cross sections with the experimental data for the reaction system$ ^{12} $ C+$ ^{194} $ Pt,$ ^{12} $ C+$ ^{198} $ Pt,$ ^{19} $ F+$ ^{188} $ Os,$ ^{16} $ O+$ ^{208} $ Pb,$ ^{12} $ C+$ ^{236} $ U,$ ^{12} $ C+$ ^{238} $ U , and$ ^{16} $ O+$ ^{238} $ U. It can be clearly seen from Fig. 1 that the theoretical results are in good agreement with the experimental data for the seven reactions. The values of the capture cross sections are calculated within a factor of three.
Figure 1. Calculated capture cross sections as functions of the excitation energy for seven reactions. The experimental data for
$^{12}$ C+$^{194}$ Pt [45],$^{12}$ C+$^{198}$ Pt [45],$^{19}$ F+$^{188}$ Os [46],$^{16}$ O+$^{208}$ Pb [47],$^{12}$ C+$^{236}$ U [48],$^{12}$ C+$^{238}$ U [49] , and$^{16}$ O+$^{238}$ U [49, 50] are denoted by open circles.It is necessary to determine the effective value of the level density parameter a in Eq. (7) and
$ E_{\rm D} $ in Eqs. (9, 10) to calculate the survival probability using Eqs. (5–7) and Eqs. (9, 10). The value of the level density parameter in Eq. (7) is an asymptotic value$ a = 0.073A+0.095A^{2/3} $ in the calculation presented in this article. In addition, the ratio$ a_{f}/a_{n} $ could, in principle, be a free parameter. However, the constant value$ a_{f}/a_{n} = 1.02 $ was used to control the variables from heavy to superheavy nuclei. The damping factor$ E_{\rm D} $ denotes the speed of scouring of the shell correction with excitation energy (temperature effects) in Eqs. (9) and (10). Furthermore, the dependence of the$ E_{\rm D} $ value on the excitation energy changes rapidly with the proton and neutron numbers. To illustrate the influence of the damping factor value$ E_{\rm D} $ on the survival probability, the values$ E_{\rm D} $ = 16.5 MeV and$ E_{\rm D} $ = 25.0 MeV were chosen to describe the speed of washing out of the shell correction with the excitation energy in Eqs. (9) and (10).If the temperature-dependent effective potential energy surface is considered, then the damping of the shell effects will affect the decay width of fission and decay width of neutron emission as per Eqs. (9) and (10). To illustrate the influence of the neutron separation energy calculated by the effective compound nucleus ground state on the survival probability, Fig. 2 shows the ERCSs of the reactions
$ ^{12} $ C+$ ^{236} $ U and$ ^{18} $ O+$ ^{248} $ Cm, when not considering (dashed lines) and considering (solid lines) the influence of the excitation energy on the neutron separation energy. It can be observed that the magnitude of the ERCSs shows no significant change when one considers the influence of the excitation energy on the neutron separation energy. However, we still need to evaluate the neutron separation energy through the effective compound nucleus ground state to ensure self-consistency of the calculation.
Figure 2. (color online) Calculated ERCSs obtained with and without considering the influence of temperature effects on the neutron separation energy are denoted by solid and dashed lines, respectively.
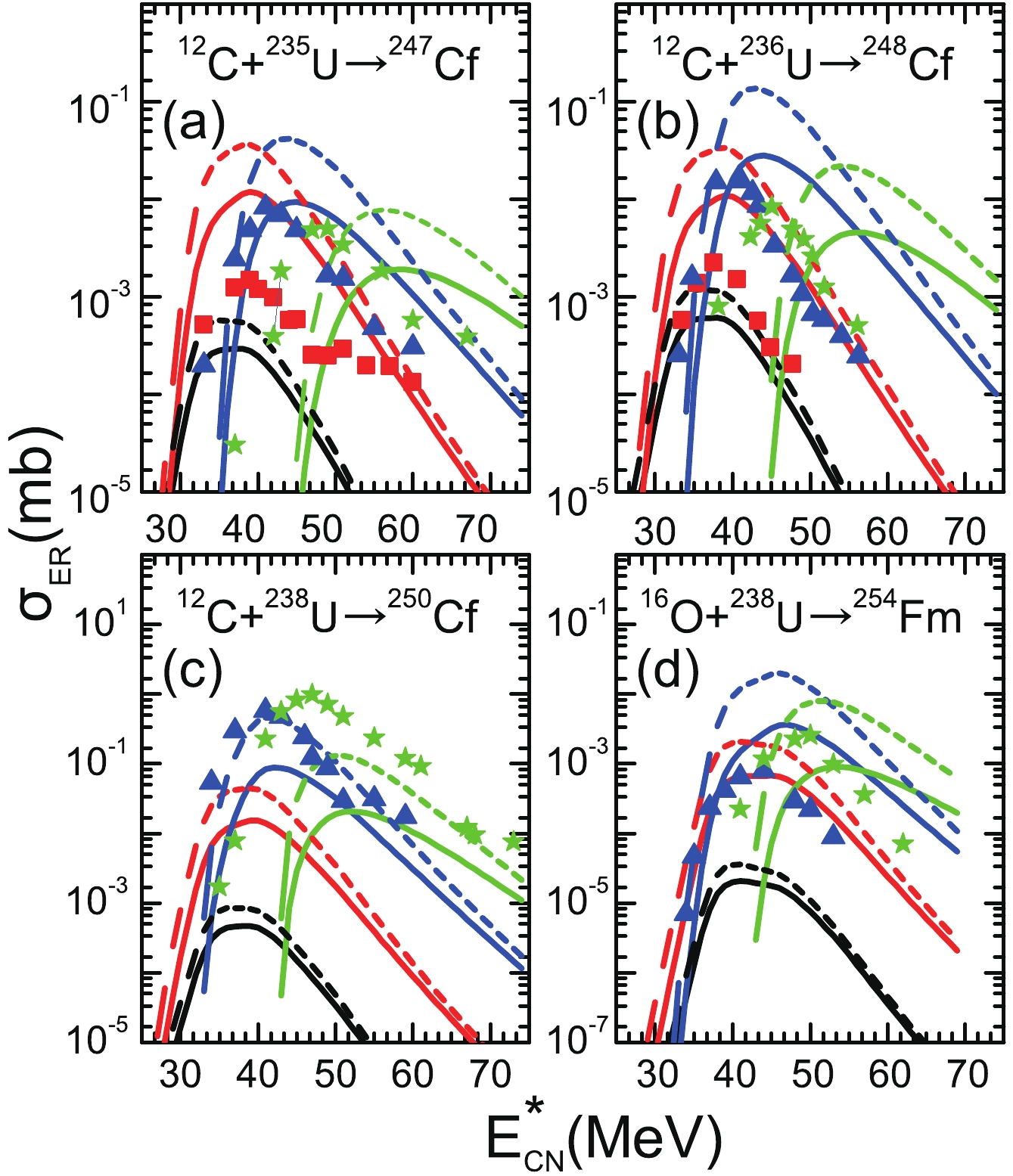
Figures 3-5 show the ERCSs of the projectile-target combination reaction system with large asymmetry in the 2n-5n channels by considering the washing out of microscopic effects with excitation energy in the potential energy surface. The measured ERCSs of the 2n, 3n, 4n, and 5n channels are denoted by filled (black) circles, filled (red) squares, filled (blue) triangles, and filled (green) pentagrams, respectively. The calculated results with the damping factor values
$ E_{\rm D} $ = 25.0 MeV and$ E_{\rm D} $ = 16.5 MeV are denoted by dashed and solid lines, respectively. It can be clearly observed from Fig. 3 that there is nearly no difference between the results of the two calculations. If the experimental uncertainties are considered, then it can be stated that the ERCSs obtained by estimating the survival probability using two different damping factors can basically reproduce the experimental ERCSs with charge number$ Z = 82-90 $ . In particular, the theoretical estimation of the 3n, 4n, and 5n evaporation channels shows good agreement with the experimental data.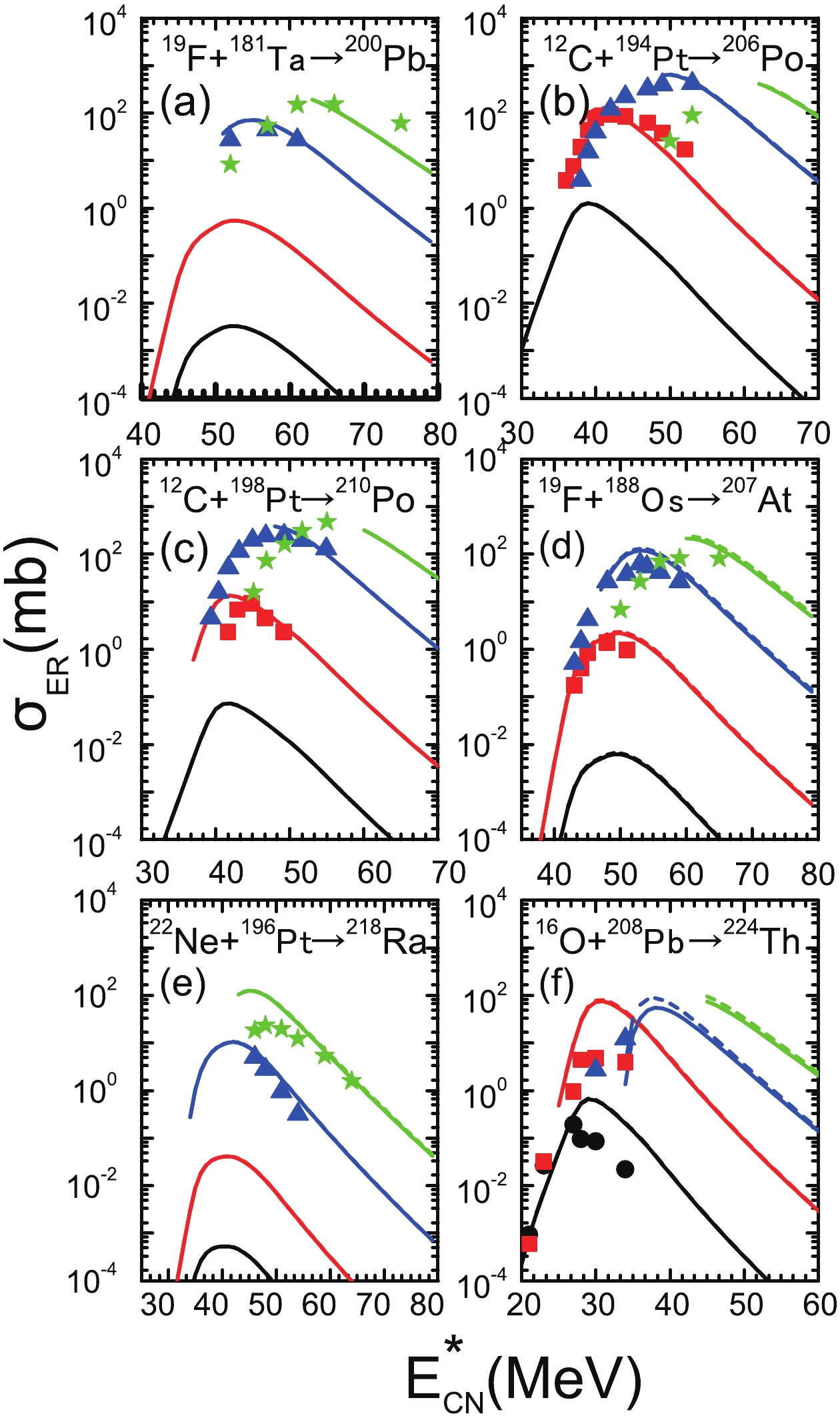
Figure 3. (color online) Comparison between the calculated ERCSs with the available experimental data for the reactions
$^{19}$ F+$^{181}$ Ta [51, 52],$^{12}$ C+$^{194}$ Pt [53],$^{12}$ C+$^{198}$ Pt [53],$^{19}$ F+$^{188}$ Os [46],$^{22}$ Ne+$^{196}$ Pt [54], and$^{16}$ O+$^{208}$ Pb [55]. The calculated results with the damping factors$E_{\rm D}$ = 25.0 MeV and$E_{\rm D}$ = 16.5 MeV are denoted by dashed and solid lines, respectively.However, it can be clearly seen from Figs. 4, 5 that there are some differences in the magnitude of the ERCSs obtained with two different damping factors to calculate the survival probability. In Fig. 4, the difference in the ERCSs for the 2n and 3n evaporation channels is approximately a factor of 3, while the 4n and 5n evaporation channels can cause an order of magnitude uncertainty. Furthermore, compared with Fig. 4, the difference between the calculated results obtained with different damping factors in Fig. 5 is further increased. This is because the component with the macroscopic and microscopic parts of the fission barrier
$ B_{\rm f} = B_{\rm f}^{\rm L D}+B_{\rm f}^{\rm M} $ has changed, and the contribution of shell correction in the fission barrier increases as the number of charges Z increases from actinide nuclei to superheavy nuclei.Taking into account the experimental uncertainties, it can be seen from Figs. 3–5 that there is good agreement between our calculated ERCSs (solid lines) and experimental values for most of the evaporation channels. In fact, we would like to point out that although some experimental data in Figs. 4, 5 do not conform to the calculations denoted by the solid lines, most of the data are still consistent, which validates the use of this set of parameters (
$ a = 0.073A+0.095A^{2/3} $ and$ E_{\rm D} $ = 16.5 MeV) to calculate the survival probability.As mentioned above, the washing out of shell effects with increasing excitation energy is introduced in the nuclear level density parameter by proposing an exponential function. To calculate the survival probability using Eqs. (5–8), it is necessary to determine the effective value of the parameters
$ \alpha $ ,$ \beta $ , and$ \gamma $ . In the present work,$ \alpha = 0.1337 $ ,$ \beta = -0.06571 $ and$ \gamma_{\rm D} = 0.04884 $ in Eq. (8) are determined by fitting the experimental data of level density based on the microscopic shell correction from FRDM1995 [42]. Therefore, these parameters should be used at the same shell correction energies to calculate the survival probability. This is because the differences between the corresponding level density parameters are mainly related to different shell corrections.To illustrate the influence of the asymptotic value of the level density parameter
$ \tilde{a}(A) $ on the survival probability, the values$ \alpha = 0.073 $ and$ \beta = 0.095 $ in Eq. (8) were also chosen to describe the level density parameter. In addition, the value$ \gamma_{\rm D} = 0.04884 $ was chosen to describe the speed of washing out of the shell correction with the excitation energy. Furthermore, it should be noted that even if the shell correction is determined, the present three parameters are not obtained by fitting the experimental data of level density.Figures 6–8 show the ERCSs of the projectile-target combination reaction system with large asymmetry in the 2n-5n channels by considering the washing out of microscopic effects with excitation energy in the level density parameter. The measured ERCSs of the 2n, 3n, 4n, and 5n channels are denoted by filled (black) circles, filled (red) squares, filled (blue) triangles, and filled (green) pentagrams, respectively. The calculated ERCSs with the two sets of parameters selected above are marked with solid lines (
$ \alpha = 0.1337 $ ,$ \beta = -0.06571 $ , and$ \gamma_{\rm D} = 0.04884 $ ) and dotted lines ($ \alpha = 0.073 $ ,$ \beta = 0.095 $ , and$ \gamma_{\rm D} = 0.04884 $ ), respectively, and compared with the available experimental data. It can be clearly observed from Fig. 6 that the calculation results of the two groups of parameters are almost identical. The theoretical estimation of the 3n, 4n, and 5n evaporation channels shows good agreement with the experimental data.
Figure 6. (color online) The same comparison as presented in Fig. 3, but the calculated results with the parameters
$\alpha = 0.1337$ ,$\beta = -0.06571$ , and$\gamma_D = 0.04884$ in Eq. (8) are denoted by solid lines, and with the parameters$\alpha = 0.073$ ,$\beta = 0.095$ , and$\gamma_D = 0.04884$ in Eq. (8) are denoted by dashed lines.
Figure 7. (color online) The same comparison as presented in Fig. 4, but the calculated results with the parameters
$\alpha = 0.1337$ ,$\beta = -0.06571$ , and$\gamma_{\rm D} = 0.04884$ in Eq. (8) are denoted by solid lines, and with the parameters$\alpha = 0.073$ ,$\beta = 0.095$ , and$\gamma_{\rm D} = 0.04884$ in Eq. (8) are denoted by dashed lines.
Figure 8. (color online) The same comparison as in Fig. 5, but the calculated results with the parameters
$\alpha = 0.1337$ ,$\beta = -0.06571$ . and$\gamma_{\rm D} = 0.04884$ in Eq. (8) are denoted by solid lines, and with the parameters$\alpha = 0.073$ ,$\beta = 0.095$ , and$\gamma_{\rm D} = 0.04884$ in Eq. (8) are denoted by dashed lines.It can be seen from Figs. 7, 8 that the difference between the results calculated with the two sets of parameters increases with increase in the number of compound nuclear charges. With respect to most of the reaction system, the results obtained with the values
$ \alpha = 0.1337 $ ,$ \beta = -0.06571 $ , and$ \gamma_{\rm D} = 0.04884 $ in Eq. (8) have systematically underestimated the experimental data for the 5n evaporation channel. In addition, the calculated ERCSs are systematically shifted towards the higher energies by approximately 4–7 MeV as compared with the experimental data. This effect is also illustrated in Ref. [24].It can be seen from Eq. (8) that the level density parameter used to calculate the fission width is independent of the change in the excitation energy. This is because it is assumed that the shell correction of the saddle point is equal to zero in Eq. (8), and the locations of the fission transition points do not change with the excitation energy. The damping of the shell effects directly influences the decay width of the neutron emission
$ \Gamma_{n} $ as opposed to the fission width. Therefore, there is no adjustable parameter when$ \alpha $ ,$ \beta $ , and$ \gamma $ are determined by fitting the experimental data of level density. However, the asymptotic value of$ \tilde{a}(A) $ ($ \tilde{a}(A) = \alpha A+\beta A^{2/3} $ ) and the damping factor$ \gamma_{\rm D} $ in the level density parameter were not consistently determined in many calculations [22-24]. Moreover, as the level density parameter in the fission channel was considered to be constant and independent of the excitation energy, it is possible to use two free parameters in the calculations: the ratio$ a_{f}/a_{n} $ and the coefficient$ C_{f} $ in the macroscopic part of the fission barrier [22, 23]. In this case, good agreement between the experiment and calculation is achieved.If some additional parameters are not introduced, some uncertainties might still remain in the calculations of the fission probability at high excitation energy, wherein we consider the influence of the washing out of shell effects with the excitation energy on the level density parameter. First, the transition states are well determined based on assumptions that might be valid in certain cases. Theoretical research has shown that the locations of the fission transition points do not significantly change at a low excitation energy range up to a temperature of 1 MeV. However, there is a dramatic change in the locations of the transition points above
$ T> $ 1 MeV [65, 66]. Therefore, as the locations of the transition points are a function of the excitation energy at high excitation energies, they might not be calculated accurately. Second, the collective motion of the system about the ground state position should be included at high excitation energies [67]. -
In summary, in this paper, the survival probability of super-asymmetric reaction systems was calculated by considering two approximate methods of the washing out of shell effects with the excitation energy, namely the excitation energy dependence of the energy density parameter, and the excitation energy dependence of the fission barrier and neutron separation energy.
When the calculated ERCSs and experimental data were compared for 16 reaction systems from heavy to superheavy nuclei, the two calculation results were in agreement with the experimental data in some reactions. Although two different possibilities of the dependence of washing out of shell effects on the excitation energy were analyzed, it is difficult to draw a strong conclusion from the analysis which approximation method is more reliable, as there are a large number of adjustable parameters and assumptions.
Moreover, we can clearly see that the calculation results of the
$ 5n $ evaporation channel obtained by considering the dependence of the energy density parameter on the excitation energy underestimated the experimental data. This is because some aspects of physics are missing from Eqs. (6) and (7), which does not allow one to derive a very accurate description of the fission probability at high excitation energy.
Analysis of survival probability based on superasymmetric reaction systems
- Received Date: 2020-04-03
- Available Online: 2020-09-01
Abstract: The survival probability of an excited compound nucleus was studied using two different approaches of the washing out of shell effects with excitation energy based on a superasymmetric reaction system. The estimated evaporation residue cross sections based on the two different methods are compared with the available experimental data. Both methods are in agreement with the experimental data to a certain extent for some specific reactions and





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: