-
The test of CP violation in the Standard Model, which is described by the complex phase in the Cabibbo-Kobayashi-Maskawa (CKM) matrix, is the central goal of the heavy flavor physics programme. Using B decays to determine the three angles
$ \alpha $ ,$ \beta $ and$ \gamma $ of the usual non-squashed unitarity triangle of the CKM matrix, and thus to test the closure of the unitarity triangle, is a straightforward and promising way to accomplish this goal. Any discrepancies would suggest possible new sources of CP violation beyond the Standard Model.In principle,
$ \alpha $ ,$ \beta $ and$ \gamma $ can be determined via the measurements of CP violating asymmetry in neutral B decays to CP eigenstates. If a single CKM amplitude or different amplitudes with the same CKM phase contribute to the decay of$ B^0 $ meson, then the mixing-induced CP asymmetry is a pure function of CKM parameters, which are derived from the two neutral B meson mixing and$ B^0 $ decay with no strong phase uncertainties. As is well known, the angle$ \beta $ can be determined in a reliable way with the help of the mixing-induced CP violation in the single "gold plated" mode$ B^0 \to J/\psi K_S $ . Likewise,$ \alpha $ can be extracted using the neutral B decay$ B^0 \to \pi^+ \pi^- $ , using the isospin symmetry to separate the tree and penguin contributions in the$ B \to \pi \pi $ decays. Similarly to the measurement of$ \beta $ and$ \alpha $ , a straightforward way to obtain$ \gamma $ theoretically might be to use the CKM suppressed$ B_s^0 $ decay$ B_s^0 \to \rho K_S $ , or to analyze the decays$ B_s^0 \to D^0 \phi,\bar{D}^0 \phi $ and$ D_1^0 \phi $ , as in [1]. However, the observed mixing-induced CP asymmetries are expected to be strongly diluted by the large$ B_s-\bar{B_s} $ mixing, so that determining$ \gamma $ in this way is considerably more involved than it is for$ \beta $ and$ \alpha $ .The third angle
$ \gamma $ is currently one of the least known. It depends on the difference between the strong phases of the amplitude contributions in B decays, which is difficult to calculate reliably. One of the theoretically best ways of determining$ \gamma $ is to use the interference between the$ b \to c \bar{u} s $ and$ b \to u\bar{c}s $ decay amplitudes, with the intermediate states$ D^0 $ and$ \bar{D^0} $ mesons subsequently decaying into common final states. Depending on the common final states, the methods can be divided into: the GLW method [2] , where D mesons decay into CP eigenstates; the ADS method [3], where the final state is not a CP eigenstate but uses the doubly Cabibbo-suppressed decays to enhance the CP violation effect; the GGSZmethod [4], which exploits the three-body D decays to self-conjugate modes, such as$ D^0 \to K_S K^+ (\pi^+) K^-(\pi^-) $ . The world average values are obtained by combining the above methods in order to reduce the statistical uncertainties, and are$ \gamma \!\!=\!\! (71.1^{+4.6}_{-5.3})^{\circ} $ [5],$ \gamma \!\!=\!\! (73.5^{+4.2}_{-5.1})^{\circ} $ [6] and$ \gamma = (70.0 \pm 4.2)^{\circ} $ [7] fitted by the HFLAV, CKMFitter and UTfit collaborations, respectively. The latest measurement of$ \gamma $ by the LHCb collaboration yielded$ (74.0^{+5.0}_{-5.8})^{ \circ} $ [8]. As of mid 2019 , the preliminary result by CKMfitter for$ \gamma $ from all sources is$ \gamma = (65.80^{+0.94}_{-1.29})^{\circ} $ [9]. As there is no penguin diagram pollution in the charmed B decays, and as the theoretical uncertainty on$ \gamma $ determined from higher-order electroweak corrections is very small, a shift$ \delta \gamma \lesssim {\cal{O}}(10^{-7}) $ calculated in [10], the uncertainty of approximately$ 5^{ \circ} $ on$ \gamma $ is statistically limited. The reason for the relatively large statistical uncertainty is due to the small branching fraction Br($ B^- \to \bar{D^0} K^- $ )$ \sim\, {\cal{O}}(10^{-6}) $ .The two-body charmless B meson decays receive contributions from the tree and penguin diagrams with relatively large branching ratios, of the order of
${\cal{O}}(10^{- 6}- $ $ 10^{- 5}) $ . The branching ratios and CP asymmetry parameters depend strongly on the interference of the tree and penguin diagrams with different weak and strong phases. This provides a possible way to measure the CKM angle$ \gamma $ . The only problem here is how to calculate or extract reliably the different strong phases of the tree and penguin diagrams of charmless B decays. The methods proposed in Refs. [11–13] extract the strong phases in the$ B\to \pi \pi $ ,$ B \to \pi K $ and$ B \to KK $ decays by using the flavor SU(3) symmetry. Fleischer proposed a method to use the decays$ B_d \to \pi^+ \pi^- $ and$ B_s \to K^+ K^- $ via the U spin flavor symmetry of strong interactions [14]. All these methods require a number of experimental measurements but do not depend on the non-perturbative QCD calculations. However, the precision of determining$ \gamma $ is limited by the theoretical uncertainties of the flavor SU(3) breaking effects or U spin breaking corrections. Some of them can only provide a bound on$ \gamma $ , and serve as a complementary and indirect constraint on the unitarity triangle. Recently, three-body charmless B decays, whose amplitudes are related by the flavor SU(3) symmetry [15–17] or U spin flavor symmetry [18], were used to extract the CKM angle$ \gamma $ . The uncertainty of this fit was of the order of$ 10^{ \circ} $ with six possible solutions found in the latest paper [17].In order to improve the precision of
$ \gamma $ angle measurements, one has to deal with the flavor SU(3) breaking effect. Recently, the factorization assisted topological amplitude approach was proposed in [19–23] to parameterize all contributions to charmless B decays by topological diagrams, but keeping most of the SU(3) breaking effects. Similarly to the previous version of the topological diagram approach [24], most of the hadronic decay amplitudes of the weak diagrams are fitted using the experimental measurements instead of the perturbative QCD calculations. Thus, the fit is model independent. We also take into account the flavor SU(3) breaking effects in each flavor topological diagram characterized by decay constants and weak transition form factors. As a result, we can reduce the number of unknown hadronic parameters by fitting all charmless two-body$ B \to PP $ ,$ PV $ decays together [19], while the study in [24] fitted the$ B \to PP $ and$ B \to PV $ decay modes separately with two sets of parameters. In the present work, we use all experimentally measured$ B \to PP $ ,$ PV $ decay observables to perform a global fit, but leave the weak phase$ \gamma $ to be fitted from the abundant experimental data together with the hadronic parameters. There are also a number of measured B decay channels with two vector meson final states. Since this kind of decay is more complicated as it includes transverse polarization, we do not include them in our current study to avoid introducing more free parameters. Therefore, in the present work, we fit 15 parameters using 37 experimentally measured branching fractions and 11 CP asymmetry parameters of the$ B \to PP $ ,$ PV $ decays.We begin in Sec. 2 with a summary of the parametrization of the tree and penguin topological amplitudes of the charmless
$ B \to PP $ $ PV $ decays, which leave the weak phase$ \gamma $ as a free parameter, to be fitted together with the hadronic parameters. The fit result of the CKM angle$ \gamma $ with the experimental and theoretical uncertainties is presented in Sec. 3, and the conclusions are given in Sec. 4. -
The charmless two-body B meson decays are induced by weak interactions via the tree diagram and the penguin diagram at the quark level. The tree level weak decay diagram contributes via the so-called color-favored tree emission diagram T, color-suppressed tree emission diagram C, W-exchange tree diagrams E, and the W annihilation tree diagrams A, which are shown in Fig. 1. The 1-loop corrections of the QCD penguin diagrams are not suppressed due to the larger CKM matrix element compared with the tree diagram. They are also grouped into four categories: (a) the QCD-penguin emission diagram P, (b) the flavor-singlet QCD-penguin diagram
$ P_C $ orEW-penguin diagram $ P_{EW} $ , (c) the time-like QCD-penguin diagram$ P_E $ , and (d) the space-like QCD-penguin annihilation diagram$ P_A $ , shown in Fig. 2.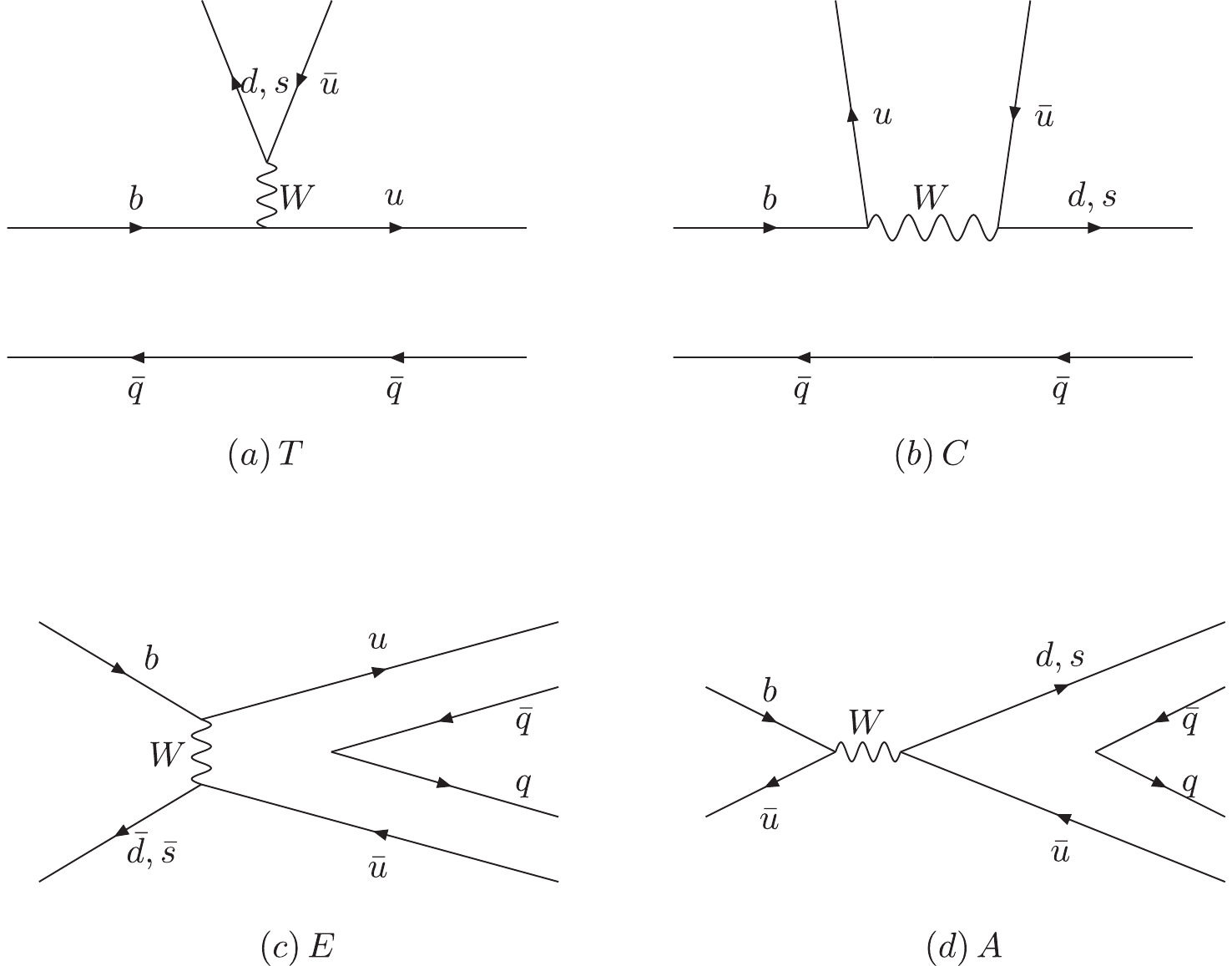
Figure 1. Topological tree diagrams contributing to
$ B\to PP $ and$ B\to PV $ decays: (a) the color-favored tree emission diagram T, (b) the color-suppressed tree emission diagram C, (c) the W-exchange diagram E , and (d) the W-annihilation diagram A.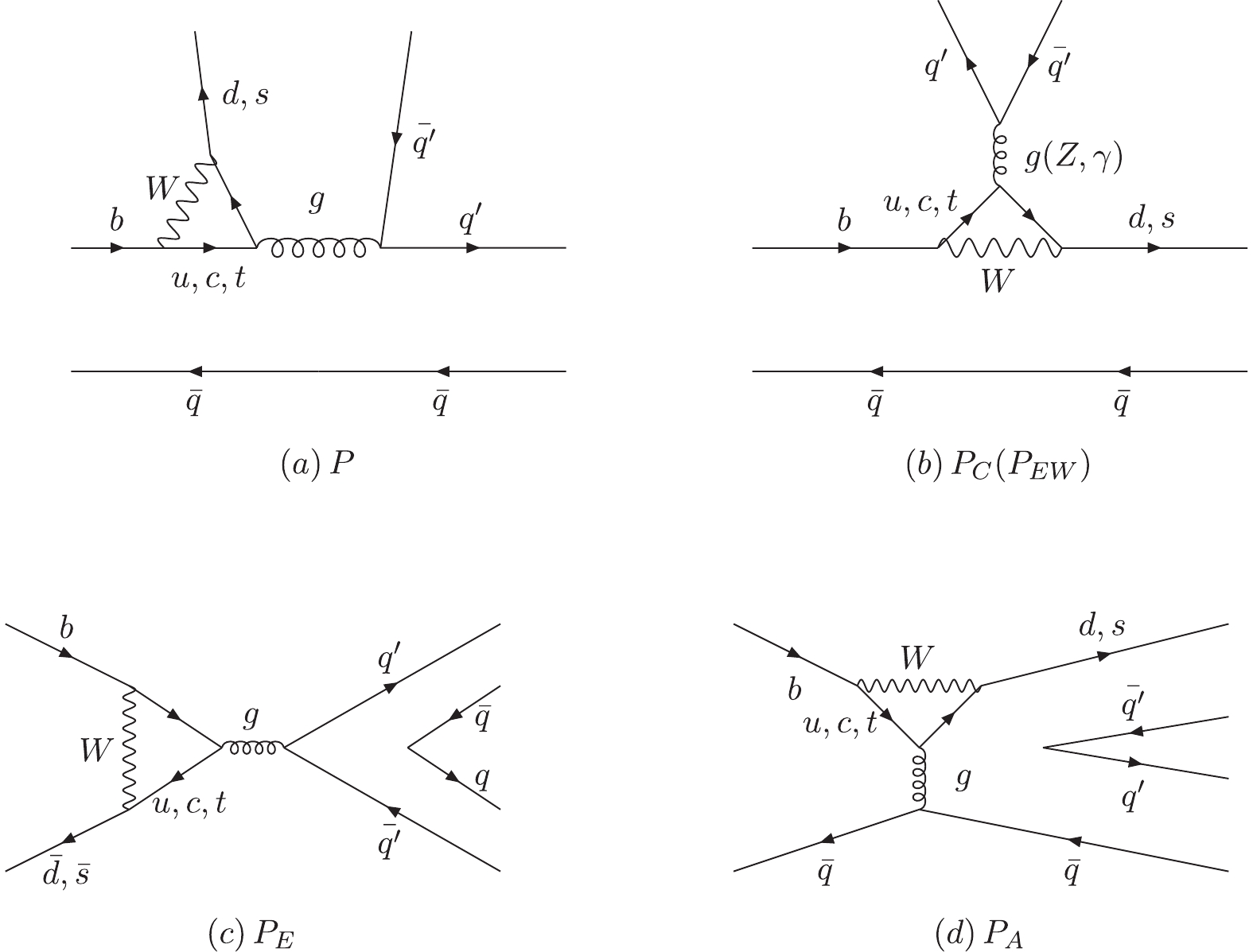
Figure 2. Topological penguin diagrams contributing to
$ B\to PP $ and$ B\to PV $ decays: (a) the QCD-penguin emission diagram P, (b) the flavor-singlet QCD-penguin diagram$ P_C $ orEW-penguin diagram $ P_{EW} $ , (c) the time-like QCD-penguin diagram$ P_E $ , and (d) the space-like QCD-penguin annihilation diagram$ P_A $ .The color-favored tree (T) topology shown in Fig. 1(a)was proven to be factorizable to all orders of
$ \alpha_{s} $ in the QCD factorization approach [25], the perturbative QCD factorization approach [26] and the soft-collinear effective theory [27], and it is easily parametrized as$ \begin{split} T^{P_{1}P_{2}} =& {\rm i}\frac{G_{F}}{\sqrt{2}}V_{ub}V^*_{uq^{'}}a_{1} (\mu)f_{p_{2}}(m_{B}^{2}-m_{p_{1}}^{2})F_{0}^{BP_{1}}(m_{p_{2}}^{2}),\\[1mm] T^{PV} =& \sqrt{2}G_{F}V_{ub}V^*_{uq^{'}}a_{1} (\mu)f_{V} m_{V}F_{1}^{B-P}(m_{V}^{2})(\varepsilon^{*}_{V}\cdot p_{B}),\\[1mm] T^{VP} =& \sqrt{2}G_{F}V_{ub}V^*_{uq^{'}}a_{1} (\mu)f_{P} m_{V}A_{0}^{B-V}(m_{P}^{2})(\varepsilon^{*}_{V}\cdot p_{B}). \end{split} $

(1) The superscript in
$ T^{P_{1}P_{2}} $ denotes that the final mesons are two pseudoscalar mesons, and in$ T^{PV(VP)} $ that the recoiling mesons are pseudoscalar meson (vector meson).$ q' = d,s $ quark in the$ \Delta S = 0,1 $ transition, respectively.$ a_1(\mu) $ is the effective Wilson coefficient from the short distance QCD corrections,$ a_1(\mu) = C_2(\mu)+C_1(\mu)/3 = 1.05 $ at next-to-leading order [28], with factorization scale$ \mu $ , insensitive to final state mesons, usually chosen at$ {m_b}/2 = 2.1 \mathrm{GeV} $ . The decay constants$ f_{P} $ ,$ f_{V} $ and the form factors$ F_{0}^{BP_{1}} $ ,$ F_{1}^{B-P} $ and$ A_{0}^{B-V} $ characterize the$ SU(3) $ breaking effects.$ \varepsilon^{*}_{V} $ is the polarization vector of vector meson, and$ p_{B} $ is the 4-momentum of B meson.We parametrize the non-factorization dominant color suppressed tree diagrams as
$ \begin{split} C^{P_{1}P_{2}} =& {\rm i}\frac{G_{F}}{\sqrt{2}}V_{ub}V^*_{uq^{'}}\chi^{C}\mathrm{e}^{{\rm i}\phi^{C}} f_{p_{2}}(m_{B}^{2}-m_{p_{1}}^{2})F_{0}^{BP_{1}}(m_{p_{2}}^{2}),\\[1mm] C^{PV} =& \sqrt{2}G_{F}V_{ub}V^*_{uq^{'}}\chi^{C^{\prime}}\mathrm{e}^{{\rm i}\phi^{C^{\prime}}} f_{V} m_{V}F_{1}^{B-P}(m_{V}^{2})(\varepsilon^{*}_{V}\cdot p_{B}), \\[1mm] C^{VP} =& \sqrt{2}G_{F}V_{ub}V^*_{uq^{'}}\chi^{C}\mathrm{e}^{{\rm i}\phi^{C}} f_{P} m_{V}A_{0}^{B-V}(m_{P}^{2})(\varepsilon^{*}_{V}\cdot p_{B}), \end{split} $

(2) where
$ \chi^{C} $ ,$ \phi^{C} $ represent the magnitude and phase of the pseudo-scalar meson emitted decays$ B\to PP $ ,$ VP $ . The prime in$ \chi^{C^{\prime}} $ ,$ \phi^{C^{\prime}} $ denotes the difference with respect to the hadronic parameters in the amplitude of the vector meson emitted decay$ B\to PV $ . Similarly, we parametrize the W exchange diagrams as$ \begin{split} E^{P_{1}P_{2}} =& {\rm i}\frac{G_{F}}{\sqrt{2}}V_{ub}V^*_{uq^{'}} \chi^{E} \mathrm{e}^{{\rm i}\phi^{E}} f_{B}m_{B}^{2}\left(\frac{f_{p_{1}}f_{p_{2}}}{f_{\pi}^{2}}\right),\\[1mm] E^{PV,VP} =& \sqrt{2}G_{F}V_{ub}V^*_{uq^{'}}\chi^{E} \mathrm{e}^{{\rm i}\phi^{E}} f_{B}m_{V}\left(\frac{f_{P}f_{V}}{f_{\pi}^{2}}\right)(\varepsilon^{*}_{V}\cdot p_{B} ), \end{split} $

(3) where
$ \chi^{E} $ ,$ \phi^{E} $ represent the magnitude and strong phase. We ignore the W annihilation topology, as its contribution is negligible, as discussed in [24].The penguin emission diagram was also proven to be factorizable to all orders of
$ \alpha_S $ in various QCD inspired approaches and the soft-collinear effective theory. Thus, its amplitudes are describe as follows:$ \begin{split} P^{PP} =& -{\rm i}\frac{G_{F}}{\sqrt{2}}V_{tb}V_{tq^{'}}^{*}\left[a_{4}(\mu)+\chi^{P}\mathrm{e}^{{\rm i}\phi^{P}}r_{\chi}\right] f_{p_{2}}(m_{B}^{2}-m_{p_{1}}^{2})\\ &\times F_{0}^{BP_{1}}(m_{p_{2}}^{2}), \\ P^{PV} =& -\sqrt{2}G_{F} V_{tb}V_{tq^{'}}^{*}a_{4}(\mu) f_{V}m_{V}F_{1}^{B-P}m_{V}^{2} (\varepsilon^{*}_{V}\cdot p_{B}), \end{split} $

$ \begin{split} P^{VP} =& -\sqrt{2}G_{F}V_{tb}V_{tq^{'}}^{*}\left[a_{4}(\mu)-\chi^{P} \mathrm{e}^{{\rm i}\phi^{P}}r_{\chi}\right] \\ &\times f_{P}m_{V}A_{0}^{B-V}(m_{P}^{2})(\varepsilon^{*}_{V}\cdot p_{B}), \end{split} $

(4) where the second terms denote the “chiral enhanced” penguin contributions, with the chiral factor of pseudo-scalar meson
$ r_{\chi} $ . The Wilson coefficient$ a_{4}(\mu) $ of effective penguin operators is calculated to the next-to-leading order [28]. We parametrize the flavor-singlet penguin diagram as$ \begin{split} P_{C}^{PP} =& -{\rm i}\frac{G_{F}}{\sqrt{2}}V_{tb}V_{tq^{'}}^{*}\chi^{P_C}\mathrm{e}^{{\rm i}\phi^{P_C}} f_{p_{2}}(m_{B}^{2}-m_{p_{1}}^{2})F_{0}^{BP_{1}}(m_{p_{2}}^{2}) ,\\ P_{C}^{PV} =& -\sqrt{2}G_{F}V_{tb}V_{tq^{'}}^{*} \chi^{P_C^{\prime}}\mathrm{e}^{{\rm i}\phi^{P_C^{\prime}}} f_{V}m_{V}F_{1}^{B-P}(m_{V}^{2})(\varepsilon^{*}_{V}\cdot p_{B}),\\ P_{C}^{VP} =& -\sqrt{2}G_{F}V_{tb}V_{tq^{'}}^{*} \chi^{P_C}\mathrm{e}^{{\rm i}\phi^{P_C}} f_{P}m_{V}A_{0}^{B-V}(m_{P}^{2})(\varepsilon^{*}_{V}\cdot p_{B}). \end{split} $

(5) Looking carefully at Fig. 2(a) and 2(d), one can see that the only difference between them is the hard gluon attached to a light quark pair. Since we do not calculate the QCD corrections but fit them to the experimental measurements, these two diagrams give the same contribution. Since the contribution of pseudo-scalar meson emission
$ P_{A}^{PP,VP} $ is already encoded in the parameters$ r_{\chi}\chi^{P} $ ,$ \mathrm{e}^{{\rm i}\phi^{P}} $ in Eq. (4) for diagram Fig. 2(a), we only have the vector meson contribution left for the space-like penguin diagrams,$ P_{A}^{PV} = -\sqrt{2}G_{F}V_{tb}V_{tq^{'}}^{*}\chi^{P_{A}}\mathrm{e}^{{\rm i}\phi^{P_{A}}} f_{B}m_{V}\left(\frac{f_{P}f_{V}}{f_{\pi}^{2}}\right)(\varepsilon^{*}_{V}\cdot p_{B}). $

(6) The contribution from the time-like penguin (
$ P_E $ ) diagram is arguably small, and can be ignored in the decay modes where it is not dominant [19].The electroweak penguin topology (
$ P_{EW} $ ) is similar to the tree and penguin emission diagrams, which can be proven by factorization. We calculate this diagram in QCD as$ \begin{align} P_{EW}^{PP}& = -{\rm i}\frac{G_{F}}{\sqrt{2}}V_{tb}V_{tq^{'}}^{*}e_{q}\frac{3}{2}a_{9}(\mu) f_{p_{2}}(m_{B}^{2}-m_{p_{1}}^{2})F_{0}^{BP_{1}}(m_{p_{2}}^{2}),\\ P_{ EW}^{PV}& = -\sqrt{2}G_{F}V_{tb}V_{tq^{'}}^{*}e_{q}\frac{3}{2}a_{9}(\mu) f_{V}m_{V}F_{1}^{B-P}(m_{V}^{2})(\varepsilon^{*}_{V}\cdot p_{B}),\\ P_{EW}^{VP}& = -\sqrt{2}G_{F}V_{tb}V_{tq^{'}}^{*}e_{q}\frac{3}{2}a_{9}(\mu) f_{P}m_{V}A_{0}^{B-V}(m_{P}^{2})(\varepsilon^{*}_{V}\cdot p_{B}), \end{align} $

(7) where
$ a_9(\mu) $ is the effective Wilson coefficient at the next-to-leading order. -
From Eqs. (1-7), one notices that all tree amplitudes are proportional to
$ V_{ub}V^*_{uq^{'}} $ while the penguin amplitudes are proportional to$ V_{tb}V_{tq^{'}}^{*} = - (V_{ub}V_{uq^{'}}^{*}+V_{cb}V_{cq^{'}}^{*}) $ . Except$ V_{ub} \equiv |V_{ub}|\, \mathrm{e}^{-{\rm i} \gamma} $ , all other CKM matrix elements$ V_{uq^{'}}^{*} $ ,$ V_{cb}V_{cq^{'}}^{*} $ are approximately real numbers without the electroweak phase. The phase angle$ \gamma $ is a free parameter to be fitted from the experimental data. The magnitudes of CKM matrix elements are input parameters from Ref. [29]$ \begin{split} |V_{ud}| & = 0.97420\pm 0.00021\, ,\; \; \; |V_{us}| = 0.2243\pm 0.0005\, ,\\[1mm] |V_{ub}| &= 0.00394\pm 0.00036\,, \;\;\; |V_{cd}| = 0.218\pm 0.004\, ,\\[1mm] |V_{cs}| &= 0.997\pm 0.017\, ,\; \; \; |V_{cb}| = 0.0422\pm 0.0008\, . \end{split} $

(8) The remaining parameters in the decay amplitude formulas are the meson decay constants and transition form factors. The meson decay constants are measured by experiments or calculated by theoretical approaches, such as the covariant light front approach [30], light-front holographic QCD [31], light-cone sum rules [32, 33], and QCD sum rules [34, 35]. We show their values in Table 1as an average from PDG [29].
$ f_{\pi} $ 

$ f_{K} $ 

$ f_{B} $ 

$ f_{\rho} $ 

$ f_{K^{*}} $ 

$ f_{\omega} $ 

$ f_{\phi} $ 

$ 130.2 \pm 1.7 $ 

$ 155.6 \pm 0.4 $ 

$ 190.9 \pm 4.1 $ 

$ 213 \pm 11 $ 

$ 220 \pm 11 $ 

$ 192\pm 10 $ 

$ 225 \pm 11 $ 

Table 1. The decay constants of light pseudo-scalar mesons and vector mesons (in unit of MeV).
The transition form factors of B meson decays are usually measured via the semileptonic B decay modes together with the CKM matrix elements. Theoretically, they are calculated in various approaches: the constitute quark model and light cone quark model [36–41], covariant light front approach (LFQM) [30, 42, 43], light-cone sum rules [33, 44–66], PQCD [67–76] and lattice QCD [77–79]. We combine these results and use the average of the transition form factors of B meson decays at
$ q^{2} $ = 0, shown in Table 2. The$ q^{2} $ dependence of the transition form factors of B meson decays are described with the dipole parametrization,$ \; \; \; F_{0}^{B \to\pi}\; \; \; $ 

$ \; \; \; F_{0}^{B\to K}\; \; \; $ 

$ \; \; \; F_{0}^{B \to\eta_{q}}\; \; \; $ 

$ \; \; \; F_{1}^{B \to\pi}\; \; \; $ 

$ \; \; \; F_{1}^{B\to K}\; \; \; $ 

$ \; \; \; F_{1}^{B \to\eta_{q}}\; \; \; $ 

$ \; \; \; A_{0}^{B \to\rho}\; \; \; $ 

$ \; \; \; A_{0}^{B\to \omega}\; \; \; $ 

$ \; \; \; A_{0}^{B\to K^{*}}\; \; \; $ 

$ F_i(0) $ 

$ 0.28 \pm 0.03 $ 

$ 0.31\pm 0.03 $ 

$ 0.21 \pm 0.02 $ 

$ 0.28\pm 0.03 $ 

$ 0.31\pm 0.03 $ 

$ 0.21 \pm 0.02 $ 

$ 0.36 \pm 0.04 $ 

$ 0.32 \pm 0.03 $ 

$ 0.39\pm 0.04 $ 

$ \alpha_1 $ 

0.50 0.53 0.52 0.52 0.54 1.43 1.56 1.60 1.51 $ \alpha_2 $ 

-0.13 -0.13 0 0.45 0.50 0.41 0.17 0.22 0.14 Table 2. The transition form factors of B meson decays at
$ q^{2} $ = 0 and dipole model parameters.$ \begin{split} F_{i}(q^{2}) = {F_{i}(0)\over 1-\alpha_{1}\displaystyle{q^{2}\over M_{\rm pole}^{2}}+ \alpha_{2}\displaystyle{q^{4}\over M_{\rm pole}^{4}}}, \end{split}$

(9) where
$ F_{i} $ denotes the form factors$ F_{0} $ ,$ F_{1} $ , or$ A_{0} $ , while$ M_{\rm pole} $ is the mass of the corresponding pole state, such as$ B_{(s)} $ for$ A_{0} $ , and$ B^{*}_{(s)} $ for$ F_{0,1} $ .$ q^2 $ of charmless B meson decays is not far from zero, thus the uncertainties of the dipole model parameters are neglected in our calculations. The dipole model parameters are also listed in Table 2.To minimize the statistical uncertainties, we use the maximum number of experimental observables of the
$ B \to PP $ ,$ PV $ decays. However, some of them were measured with very poor precision. Hence, we do not use in our fit those measurements with less than a$ 3\sigma $ significance. As a result, we have a total of 37 branching ratios and 11 CP violation observations for the$ B \to PP $ ,$ PV $ decays shown in Table 3 and Table 4, respectively, taken from the experimental data in Ref. [29], and the 2019 by averaging the measurements from LHCb [80–82], BELLE [83] and BABAR [84] and so on.Mode Amplitudes $ {\rm {Exp}} $ 

Mode Amplitudes $ {\rm {Exp}} $ 

$ \pi^{-} \pi^{0} $ 

$ T,C,P_{EW} $ 

$ 5.5\pm0.4 $ 

$ \pi^{+} \rho^{-} $ 

$ T,E,P,(P_E),P_A $ 

$ 14.6\pm1.6 $ 

$ \pi^{-} \eta $ 

$ T,C,P,P_C,P_{EW} $ 

$ 4.02\pm0.27 $ 

$ \pi^{-} \rho^{+} $ 

$ T,E,P,(P_E) $ 

$ 8.4\pm1.1 $ 

$ \pi^{-} \eta^{'} $ 

$ T,C,P,P_C,P_{EW} $ 

$ 2.7\pm0.9 $ 

$ \pi^{0} \rho^{0} $ 

$ C,C^{\prime},E,P,P_A,(P_E),P_{EW} $ 

$ 2\pm0.5 $ 

$ \pi^{+} \pi^{-} $ 

$ T,E,(P_E),P $ 

$ 5.12\pm0.19 $ 

$ \pi^{-} \bar{K^{*0}} $ 

$ P,P_A $ 

$ 10.1\pm0.9 $ 

$ \pi^{0} \pi^{0} $ 

$ C,E,P,(P_E),P_{EW} $ 

$ 1.59\pm0.26 $ 

$ \pi^{0} K^{*-} $ 

$ T,C,P,P_A,P_{EW} $ 

$ 8.2\pm1.9 $ 

$ K^{-} K^{0} $ 

$ P $ 

$ 1.31\pm0.17 $ 

$ \eta K^{*-} $ 

$ T,C,P,P_C,P_A,P_{EW} $ 

$ 19.3\pm1.6 $ 

$ K^{0} \bar{K^{0}} $ 

$ P $ 

$ 1.21\pm0.16 $ 

$ K^{-} \rho^{0} $ 

$ T,C^{\prime},P,P_{EW} $ 

$ 3.7\pm0.5 $ 

$ \pi^{-} \bar{K^{0}} $ 

$ P $ 

$ 23.7\pm0.8 $ 

$ K^{-} \omega $ 

$ T,C^{\prime},P,P_C^{\prime},P_{EW} $ 

$ 6.5\pm0.4 $ 

$ \pi^{0} K^{-} $ 

$ T,C,P,P_{EW} $ 

$ 12.9\pm0.5 $ 

$ K^{-} \phi $ 

$ P,P_C^{\prime},P_A,P_{EW} $ 

$ 8.8^{+0.7}_{-0.6} $ 

$ \eta K^{-} $ 

$ T,C,P,P_C,P_{EW} $ 

$ 2.4\pm0.4 $ 

$ \bar{K^{0}} \rho^{-} $ 

$ P $ 

$ 7.3^{+1.0}_{-1.2} $ 

$ \eta^{'} K^{-} $ 

$ T,C,P,P_C,P_{EW} $ 

$ 70.6\pm2.5 $ 

$ \pi^{+} K^{*-} $ 

$ T,P,P_A $ 

$ 8.4\pm0.8 $ 

$ \pi^{+} K^{-} $ 

$ T,P $ 

$ 19.6\pm0.5 $ 

$ \pi^{0} \bar{K^{*0}} $ 

$ C,P,P_A,P_{EW} $ 

$ 3.3\pm0.6 $ 

$ \pi^{0} \bar{K^{0}} $ 

$ C,P,P_{EW} $ 

$ 9.9\pm0.5 $ 

$ \eta \bar{K^{*0}} $ 

$ C,P,P_C,P_A,P_{EW} $ 

$ 15.9\pm1 $ 

$ \eta \bar{K^{0}} $ 

$ C,P,P_C,P_{EW} $ 

$ 1.23^{+0.27}_{-0.24} $ 

$ \eta^{'} \bar{K^{*0}} $ 

$ C,P,P_C,P_C^{\prime},P_A,P_{EW} $ 

$ 2.8\pm0.6 $ 

$ \eta^{'} \bar{K^{0}} $ 

$ C,P,P_C,P_{EW} $ 

$ 66\pm4 $ 

$ K^{-} \rho^{+} $ 

$ T,P $ 

$ 7\pm0.9 $ 

$ \pi^{-} \rho^{0} $ 

$ T,C^{\prime},P,P_A,P_{EW} $ 

$ 8.3\pm1.2 $ 

$ \bar{K^{0}} \rho^{0} $ 

$ C^{\prime},P,P_{EW} $ 

$ 4.7\pm0.6 $ 

$ \pi^{-} \omega $ 

$ T,C^{\prime},P,P_C^{\prime},P_A,P_{EW} $ 

$ 6.9\pm0.5 $ 

$ \bar{K^{0}} \omega $ 

$ C^{\prime},P,P_C^{\prime},P_{EW} $ 

$ 4.8\pm0.4 $ 

$ \pi^{0} \rho^{-} $ 

$ T,C,P,P_A,P_{EW} $ 

$ 10.9\pm1.4 $ 

$ \bar{K^{0}} \phi $ 

$ P,P_C^{\prime},P_A,P_{EW} $ 

$ 7.3\pm0.7 $ 

$ \eta^{'} \rho^{-} $ 

$ T,C,P,P_C,P_A,P_{EW} $ 

$ 9.7\pm2.2 $ 

Table 3. Branching fractions
$ (\times10^{-6}) $ of the various$ \bar B \to PP, PV $ decay modes with the decay amplitudes listed in the second column.Mode $ {{\cal{A}}_{\rm {exp}} } $ 

$ \mathcal{S_{\rm {exp}} } $ 

Mode $ {{\cal{A}}_{\rm {exp}} } $ 

$ \mathcal{S_{\rm {exp}} } $ 

$ \pi^{+} \pi^{-} $ 

0.31±0.05 −0.67±0.06 $ K_s \omega $ 

0.7±0.21 $ \pi^{0} K_s $ 

0.58±0.17 $ K_s \phi $ 

0.59±0.14 $ \eta^{'} K_s $ 

0.63±0.06 $ K^{-} \rho^{0} $ 

0.37±0.10 $ \eta K^{-} $ 

−0.37±0.08 $ \pi^{+} K^{*-} $ 

−0.22±0.06 $ \pi^{+} K^{-} $ 

−0.082±0.006 $ \eta \bar{K^{*0}} $ 

0.19±0.05 Table 4. The direct CP asymmetries (
$ {{\cal{A}}_{\rm {exp}} } $ ) and the mixing-induced CP asymmetries ($ \mathcal{S_{\rm {exp}} } $ ) in the$ \bar B\to PP, PV $ decays.We use the
$ \chi^2 $ fit method of the Minuit program [85], where the$ \chi^2 $ function is defined in terms of n experimental observables$ x_i \pm \Delta x_i $ and the corresponding theoretical values$ x_i^{\mathrm{th}} $ as$ \begin{split} \chi^{2} = \sum\limits_{i = 1}^{n}\left(\frac{x_i^{\rm th}-x_i}{\Delta x_i}\right)^2 . \end{split}$

(10) The theoretical values are written as functions of the 15 theoretical parameters of the topological amplitudes. The best fit parameters are
$ \begin{array}{clcl} \gamma &\hspace{-3mm}= (69.8 \pm 2.1)^{ \circ} , \\[1mm] \chi^{C} &\hspace{-3mm}= 0.41 \pm 0.06,\; \; \; &\phi^{C} & \hspace{-3mm}= -1.74 \pm 0.09, \\[1mm] \chi^{C^{\prime}} &\hspace{-3mm}= 0.40 \pm 0.17,\; \; \; & \phi^{C^{\prime}} &\hspace{-3mm} = 1.78\pm 0.10, \\[1mm] \chi^{E} &\hspace{-3mm}= 0.06\pm0.006,\; \; \; &\phi^{E} &\hspace{-3mm} = 2.76\pm 0.13,\\[1mm] \chi^{P} &\hspace{-3mm}= 0.09\pm0.003,\; \; \;& \phi^{P} &\hspace{-3mm} = 2.55\pm 0.03 ,\\[1mm] \chi^{P_C}&\hspace{-3mm}= 0.045 \pm 0.003,\; \; \; &\phi^{P_C} &\hspace{-3mm} = 1.53 \pm 0.08, \\[1mm] \chi^{P_C^{\prime}} &\hspace{-3mm}= 0.037\pm 0.003,\; \; \; & \phi^{P_C^{\prime}} &\hspace{-3mm} = 0.67 \pm 0.08, \\[1mm] \chi^{P_A} &\hspace{-3mm}= 0.006\pm0.0008,\; \; \; & \phi^{P_A} &\hspace{-3mm} = 1.49\pm 0.09, \end{array} $

(11) with
$ \chi^{2}/\text{d.o.f} = 45.4/33 = 1.4 $ . The uncertainties of the parameters shown above are given by the$ \chi^2 $ fit program Minuit, and are mainly due to the experimental statistical and systematic uncertainties. There are also theoretical uncertainties of the extracted$ \gamma $ values. The major source of theoretical uncertainties in our calculations are the uncertainties of the input parameters:$ |V_{ub}| $ ,$ |V_{cb}| $ , hadronic form factors and decay constants. We repeated the fit by varying the input parameters one by one assuming their Gaussian distribution. The theoretical uncertainties of$ \gamma $ were then assessed using the distribution of the central values of$ \gamma $ form these fits. The values of the theoretical uncertainty$ \sigma_{\mathrm{(T.)}} $ obtained are$ 0.2{^\circ} $ ,$ 0.2^{\circ} $ ,$ 0.9^{\circ} $ and$ 0.1^{\circ} $ from the uncertainties of$ |V_{ub}| $ ,$ |V_{cb}| $ , form factors and decay constants, respectively. The total theoretical uncertainty is$ 0.9^{\circ} $ . Our final result for$ \gamma $ is then$ (69.8 \pm 2.1 \pm 0.9) ^{\circ} $ , which is in good agreement with the current world averages:$ \gamma = (71.1^{+4.6}_{-5.3})^{\circ} $ [5],$ \gamma = (73.5^{+4.2}_{-5.1})^{\circ} $ [6] and$ \gamma = (70.0 \pm 4.2)^{\circ} $ [7], and the latest measurement of$ (74.0^{+5.0}_{-5.8})^{\circ} $ by the LHCb collaboration [8]. It is obvious that our uncertainties of$ \gamma $ are reduced to roughly a half of the uncertainties of the world-average values. -
The charmless B meson decays receive contributions from the tree amplitudes and the loop penguin amplitudes. The interference between these amplitudes makes the branching ratios of these decay modes sensitive to the CKM angles, where large direct CP asymmetries are observed. Since non-perturbative dynamics is involved, the hadronic matrix elements of these decays are difficult to calculate precisely. We parametrized the decay amplitudes of the topological diagrams, which can be fitted by the experimentally measured quantities, such as the branching ratios and CP asymmetry parameters. To improve the precision of the global fit, we factorized the corresponding decay constants and form factors in order to characterize the flavor SU(3) breaking effect. We extracted the CKM weak angle
$ \gamma $ using the measured two-body charmless$ B\to PP $ ,$ PV $ decays in the factorization assisted topological amplitude approach. The value obtained is$ (69.8 \pm 2.1 \pm 0.9) ^{\circ} $ , where the first uncertainty is from the experimental errors and the second from the hadronic parameters and CKM matrix elements. This result is compatible with the current world average values and the latest measurement of$ (74.0^{+5.0}_{-5.8})^{\circ} $ by the LHCb collaboration, but has a smaller uncertainty.We are grateful to Wen-Bin Qian and Xiao-Rui Lyu for useful discussion.
Extraction of the CKM phase γ from the charmless two-body B meson decays
- Received Date: 2020-01-08
- Available Online: 2020-06-01
Abstract: Using all experimentally measured charmless






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: