-
The nuclear mass is of crucial importance not only in nuclear physics [1], but also in weak-interaction studies and astrophysics [2, 3]. With the development of radioactive ion facilities, the nuclear masses of more than 2000 nuclei have been determined precisely [4–7]. Although considerable advancement in the precise mass measurements has been made, the majority of neutron-rich nuclei far from the valley of stability are still beyond the experimental capabilities. Therefore, a reliable theoretical nuclear mass model is crucial for their understanding.
The first theoretical study of nuclear masses can be traced back to the mass formula of von Weizäscker in 1935 [8]. This formula is a macroscopic mass formula, which neglects microscopic effects, and it shows systematic deviations for magic nuclei, and for nuclei with large deformations. In order to include the microscopic correction energy in the macroscopic mass formula, many "macroscopic-microscopic" models have been proposed, such as the finite-range droplet model (FRDM) [9], the extended Thomas-Fermi plus Strutinsky integral (ETFSI) model [10], the Koura-Tachibana-Uno-Yamada (KTUY) model [11], and the Weizäscker-Skyrme (WS) model [12, 13]. On the other hand, considerable effort has been devoted to the development of microscopic mass models. Although these models are more complicated and time consuming, large-scale calculations of microscopic mass models have become possible, and have received much attention with the development of the computer technology in recent years. For example, a series of Hartree-Fock-Bogoliubov (HFB) mass models has been proposed, based on nonrelativistic density functional theory (DFT) [14–16].
In the past decades, the covariant density functional theory (CDFT) has been used successfully to describe various nuclear properties [17–23] , and has also been applied in astrophysical calculations [24–28]. It includes the nucleonic spin degree of freedom naturally, and results automatically in the nuclear spin-orbit potential in a covariant way with an empirical strength. Also, it can provide the origin of the spin and pseudospin symmetry in the nucleon spectrum [29–38], and the spin symmetry in the anti-nucleon spectrum [39–41]. Therefore, it is interesting to investigate the nuclear mass based on CDFT. Using the TMA effective interaction and the zero-range
$ \delta $ pairing force, all nuclear masses from 16O to 331Fm were calculated based on CDFT [42], and the rms deviation with respect to known masses is about 2 MeV. Recently, a new effective interaction PC-PK1 was proposed [43], which was successfully used in describing many nuclear properties, such as$ \beta $ -decay half-lives [44, 45], fission barriers [46], nuclear quadrupole moments [47], nuclear rotations [48], low-lying spectrum [49], nuclear multiple chirality [50], etc. By applying PC-PK1 in systematic calculations of nuclear masses, it was found that the rms deviation with respect to the known masses is significantly reduced, and is only about 1 MeV [51–54].It is well-known that the pairing correlation plays an important role in describing the masses of open-shell nuclei, especially for those nuclei near the drip lines, since the Fermi surface of these nuclear systems is usually close to the continuum threshold, and hence the pairing correlation can provide a significant coupling between the bound states and the continuum states. In Refs. [55, 56], the relativistic continuum Hartree-Bogoliubov (RCHB) theory was developed, which can provide a proper treatment of pairing correlations and mean-field potentials in the presence of continuum. With the RCHB theory, the halo in 11Li was successfully reproduced in a self-consistent picture [55], and the giant halo in the light and medium-heavy nuclei was predicted in Refs. [57, 58]. In addition, the RCHB model was extended to deal with the odd nucleon system [59], and to reproduce the charge-changing cross-sections from carbon (C) to fluorine (F) isotopes on a carbon target by a combination with the Glauber model [60]. In Ref. [61], the RCHB model was used to investigate the impact of continuum on the nuclear chart, from O to Ti, and the nuclear landscape from O and Ti was remarkably extended. Lately, systematic spherical calculations for all nuclei from Z = 8 to Z = 120 were preformed by using the RCHB model with the relativistic density functional PC-PK1, and a remarkable extension of the nuclear landscape was predicted in particular for the neutron-rich side [62]. It was found that the coupling between the bound states and continuum due to the pairing correlations is important for studying the nuclear landscape [62]. In addition, an axially deformed RHB theory in continuum was developed, in which the deformation effects and continuum contribution are both considered [63, 64]. Recently, a multi-dimensional constrained relativistic mean field (MDC-RMF) model and a multi-dimensional constrained relativistic Hartree-Bogoliubov (MDC-RHB) model were also developed [65, 66], and both show the importance of deformation effects for the description of various nuclear properties.
Although the RCHB model has achieved great success, its accuracy is still far from the requirements of astrophysical applications due to fact that the deformation effects are neglected in the present calculations [62]. Therefore, it is necessary to explore new schemes to further improve the accuracy of the mass model. The radial basis function (RBF) approach [67–71], and the Bayesian neural network (BNN) approach [72–75], have been widely employed to improve nuclear mass predictions of various theoretical models, and the rms deviation with respect to the known masses has been significantly reduced. The mass correlations in the RBF approach were carefully investigated based on various nuclear mass models, and RBF provided a very effective tool for improving the mass predictions in regions not very far from known nuclear masses [68]. Lately, the RBF approach was further developed towards the so-called RBFoe approach, which includes the odd-even effects, and it was found that RBFoe can significantly improve the nuclear mass predictions after eliminating the odd-even deviations in the RBF predictions [70, 71].
Therefore, it is interesting to employ the RBFoe approach to improve the RCHB mass predictions by simulating the deformation effects and the odd-even effects, which are missing in the present RCHB mass predictions. The corresponding results and discussion are presented in Sec. III. A brief introduction to the RBF approach is given in Sec. II. The summary and perspectives are given in Sec. IV.
-
The RBF approach has been widely used to improve nuclear mass predictions [67–71]. The solution of the RBF approach is
$ S(x) = \sum\limits_{i = 1}^m {\phi} (\parallel x-x_{i}\parallel) \omega _{i}, $

(1) where
$ \parallel x-x_{i}\parallel $ is the Euclidean norm between point x and center$ x_{i} $ , and m is the number of data to be fitted. The weights$ \omega_{i} $ are determined by training RBF with m samples ($ x_{i} $ ,$ d_{i} $ ), which can be determined by$ \left( {\begin{array}{*{20}{c}} {{\omega _1}}\\ {{\omega _2}}\\ {...}\\ {{\omega _m}} \end{array}} \right){\rm{ }} = {\rm{ }}{\left( {\begin{array}{*{20}{c}} {{\phi _{11}}}&{{\phi _{12}}}&{...}&{{\phi _{1m}}}\\ {{\phi _{21}}}&{{\phi _{22}}}&{...}&{{\phi _{2m}}}\\ {...}&{...}&{...}&{...}\\ {{\phi _{m1}}}&{{\phi _{m2}}}&{...}&{{\phi _{mm}}} \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} {{d_1}}\\ {{d_2}}\\ {...}\\ {{d_m}} \end{array}} \right),{\rm{ }}$

(2) where
$ \phi _{ij} = \phi (\parallel x_i -x_j\parallel) (i,j = 1,...,m) $ .As in Refs. [68, 70], the basis function
$ \phi(r) = r $ is adopted, where the distance r between nuclei$ (Z_{i},N_{i}) $ and$ (Z_{j},N_{j}) $ in the nuclear chart is defined as$ r = \sqrt{(Z_{i}-Z_{j})^{2}+(N_{i}-N_{j})^{2}}. $

(3) Here, the mass difference
$ \Delta M(Z,N) \!=\! M_{\rm{exp}}(Z,N)\!-\!M_{\rm{th}}(Z,N) $ between the experimental and theoretical nuclear masses is adopted to reconstruct the samples for obtaining the weights with Eq. (2). The reconstructed function$ S(Z,N) $ can then be calculated with Eq. (1) for any nucleus$ (Z,N) $ . The revised mass for nucleus$ (Z,N) $ is given by$ M_{\rm{th}}^{\rm{RBF}}(Z,N) = M_{\rm{th}}(Z,N) +S(Z,N). $

(4) To evaluate the predictive power of the RBF approach, the rms deviation is calculated as
$ \sigma _{\rm{rms}} = \sqrt{\frac{1}{n}\sum\limits_{i = 1}^n {} ( M_{\rm{th}}^{i} -M_{\exp }^{i})^{2}}, $

(5) where
$ M_{\rm{th}} $ and$ M_{\rm{exp}} $ are the theoretical and experimental nuclear masses, respectively, and n denotes the number of nuclei with$ N, Z\geqslant8 $ . The experimental data are taken from the atomic mass evaluation of 2016 (AME16) [76].The theoretical masses are taken from the RCHB mass model calculated with the PC-PK1 effective interaction [43]. To further eliminate the odd-even staggering, the data were separated into four different groups, characterized by the different odd-even parities (even Z, even N), (even Z, odd N), (odd Z, even N) and (odd Z, odd N). The systematic deviations for the e-e, e-o, o-e and o-o nuclei were further reduced after training RBF separately for these four groups. The RBF approach that considers the odd-even effects is the so-called RBFoe approach, Refs. [70, 71].
-
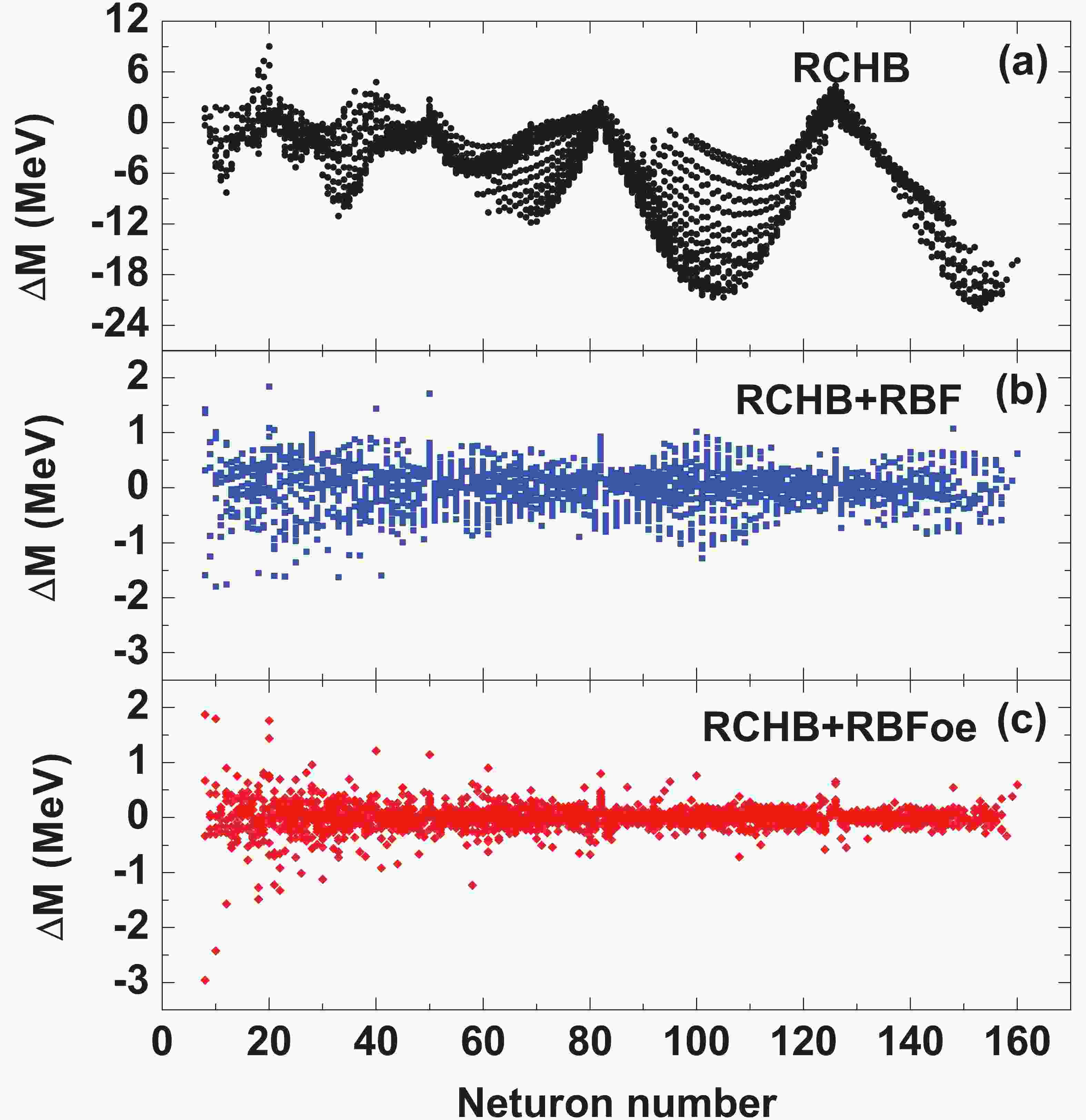
To improve the predictive power of the RCHB mass model, we first construct the function
$ S(N,Z) $ by using the known masses from AME16 [76]. The mass differences between the experimental data and the RCHB+RBF predictions are shown in Fig. 1(b). Furthermore, the predictions of RCHB+RBF are improved by using the RBFoe approach, and the corresponding mass differences between the experimental data and the RCHB+RBFoe predictions are shown in Fig. 1(c). For comparison, the mass differences using the RCHB model are shown in Fig. 1(a). From Fig. 1(a), it is seen that the RCHB mass model can describe well the masses of magic nuclei, while it generally overestimates the masses of non-magic nuclei. The overestimation of nuclear masses can be understood since the deformation effects are neglected in the present RCHB mass calculations. After introducing the improvements of the RBF approach, the mass deviations in Fig. 1(a) are reduced by about one order of magnitude, especially for non-magic nuclei. By considering in addition the RBFoe approach, it is found that the mass deviations are further reduced, and that the deviations are generally within 0.5 MeV.
Figure 1. (color online) Mass difference (
$ \Delta M$ ) between the experimental data and the predictions of (a) RCHB, (b) RCHB+RBF, and (c) RCHB+RBFoe models, as a function of the neutron number.Apart from the nuclear mass, nuclear single-nucleon separation energy is another important physical quantity used to test the accuracy of nuclear models. Taking the single-neutron separation energy
$ S_n $ as an example, the difference of the single-neutron separation energy between the experimental data and theoretical results is shown in Fig. 2. From Fig. 2(a), it is clear that the deviations of$ S_n $ are generally within 2 MeV for the RCHB predictions. Moreover, it is found that$ \Delta S_{n} $ jumps from a negative to a positive value when the neutron number N crosses a magic number. With RBF, the jumps at magic numbers are fully eliminated, as shown in Fig. 2(b), while the improvements of the magnitude of$ \Delta S_{n} $ are not obvious. By including the RBFoe approach,$ \Delta S_{n} $ is significantly reduced, as shown in Fig. 2(c), and its magnitude is generally within 1 MeV, and even less than 0.5 MeV for heavy nuclei.
Figure 2. (color online) Same as Fig. 1, for the single-neutron separation energy
$ {S_n}$ .In order to show the improvement of nuclear mass predictions more clearly, the mass difference between the experimental data and theoretical predictions are shown in Fig. 3 for all nuclei. It is found that the RCHB model generally reproduces well the experimental data for nuclei around the magic numbers, although it underestimates nuclear masses for some nuclei around N = 20 and N = 126. However, RCHB generally overestimates the masses of nuclei away from the magic numbers, and the mass deviations are generally larger than 3 MeV. The large rms deviation of the RCHB mass model is strongly associated to the deformation effect, as noted in Ref. [62]. By including the RBF approach, the mass differences are significantly reduced, and
$ \sigma_{\rm{rms}} $ decreases from 7.923 MeV to 0.386 MeV for all known nuclei from AME16 with$ Z, N\geqslant 8 $ . This means that the shell effect and the deformation effect, which are related to the underestimation and overestimation of nuclear masses mentioned above, can be simulated well with the RBF approach. However, the remaining mass differences show obvious odd-even staggering, that is the mass differences of the RCHB+RBF model appear with smaller and larger values alternatively. By further including RBFoe, the odd-even staggering is eliminated, and$ \sigma_{\rm{rms}} $ is reduced from 0.386 MeV to 0.229 MeV. This is even better than the accuracy of the sophisticated nuclear mass models, such as FRDM [9] and WS [12]. This indicates that the RBFoe approach can be employed to improve the odd-even staggering of mass differences, which originates in the drawbacks in modeling of the pairing effect.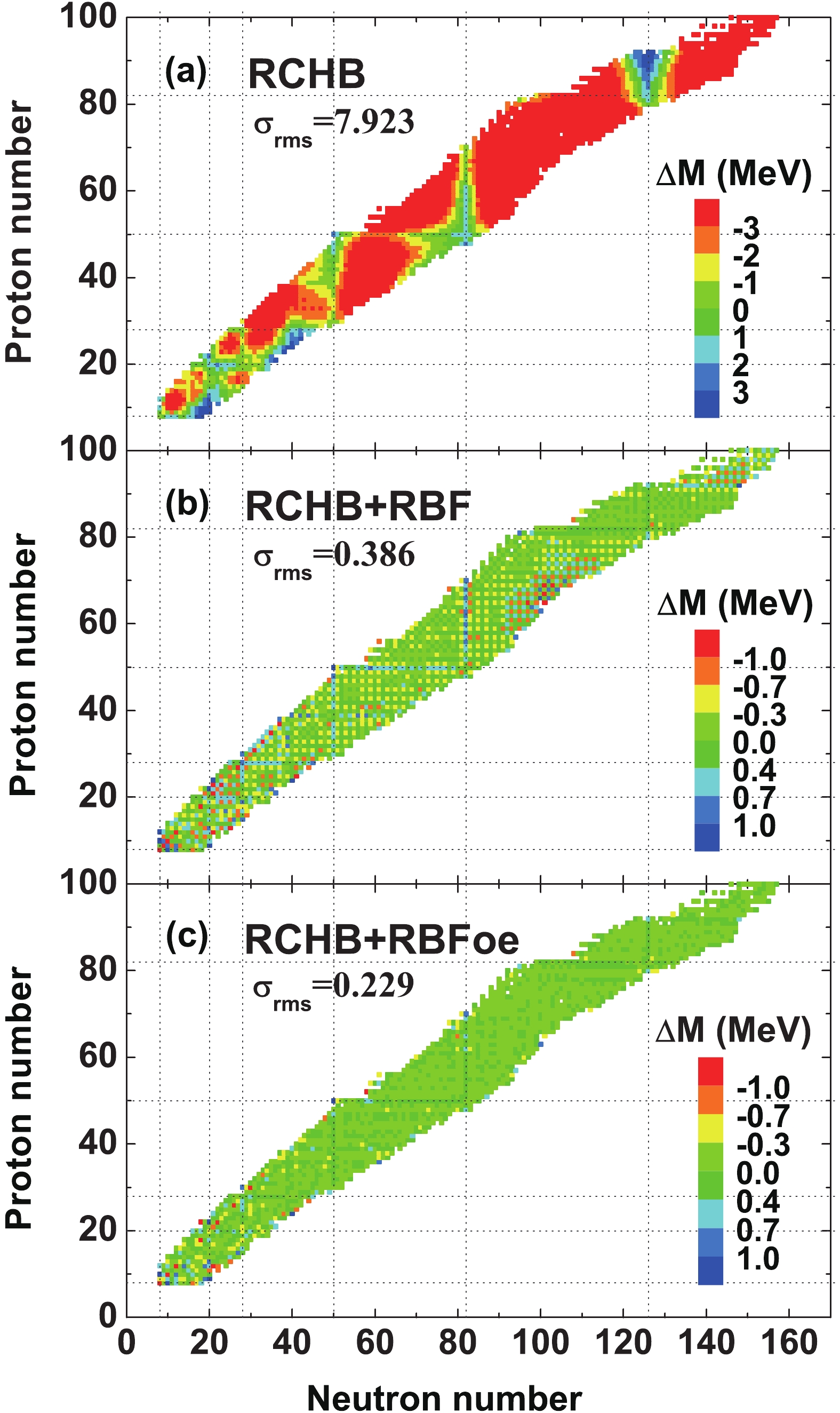
Figure 3. (color online) Mass difference between the experimental data and the predictions of (a) RCHB, (b) RCHB+RBF, and (c) RCHB+RBFoe models.
The deformation effect, the shell effect, and the pairing effect are all very important for accurate nuclear mass predictions. In the following, we discuss how the RBF and RBFoe approaches improve the description of these effects in the RCHB model. In Fig. 4, we show the rms deviation
$ \sigma_{\rm{rms}} $ of different nuclear mass models as a function of absolute value of the quadrupole deformation parameter$ |\beta_{2}| $ , where$ |\beta_{2}| $ values are taken from the HFB-31 model [77]. It is found that$ \sigma_{\rm{rms}} $ of the RCHB model increases monotonously with$ |\beta_{2}| $ , which clearly shows that large$ \sigma_{\rm{rms}} $ is associated with the missing deformation effect in the RCHB model. With the improvements brought by RBF and RBFoe,$ \sigma_{\rm{rms}} $ is significantly reduced, especially for deformed nuclei. This indicates that the deformation effect can be improved by the RBF and RBFoe approaches. The resulting trend of$ \sigma_{\rm{rms}} $ as a function of$ |\beta_{2}| $ for the RCHB+RBFoe model is similar to that of the HFB-31 model, while the trend of$ \sigma_{\rm{rms}} $ is flat for the WS4 [78] model. This may imply that some effects, which are important for the (nearly) spherical nuclei with$ |\beta_2|<0.05 $ , cannot be described well even with the RBFoe approach.
Figure 4. (color online) rms deviation
$\sigma_{\rm{rms}}$ of nuclear masses from different models with respect to the experimental data as a function of absolute value of the quadrupole deformation parameter$|\beta_{2}|$ . The point at$|\beta_{2}|=x_{0}$ represents$\sigma_{\rm{rms}}$ for nuclei with$x_{0}\leqslant|\beta_{2}|<x_{0}+0.05$ . The$|\beta_{2}|$ values are taken from HFB-31 [77].From Fig. 4, it is found that the RBF approach reduces
$ \sigma_{\rm{rms}} $ not only for deformed nuclei, but also for spherical nuclei. The improvement of$ \sigma_{\rm{rms}} $ for spherical nuclei is mainly related to the shell effect. To investigate the improvement in the shell effect with the RBF approach, the neutron shell gap for N = 50, N = 82, and N = 126 isotonic chains is shown in Fig. 5 for the RCHB mass predictions, and with RBF and RBFoe. Clearly, the RCHB model systematically overestimates the shell gap, which is also the case for the other relativistic models [42, 51]. The overestimated shell gap can be significantly reduced with the RBF approach, while the improvement with the RBFoe approach is negligible. Hence,$ \sigma_{\rm{rms}} $ for spherical nuclei in Fig. 4 is almost the same for the RCHB+RBF and RCHB+RBFoe models.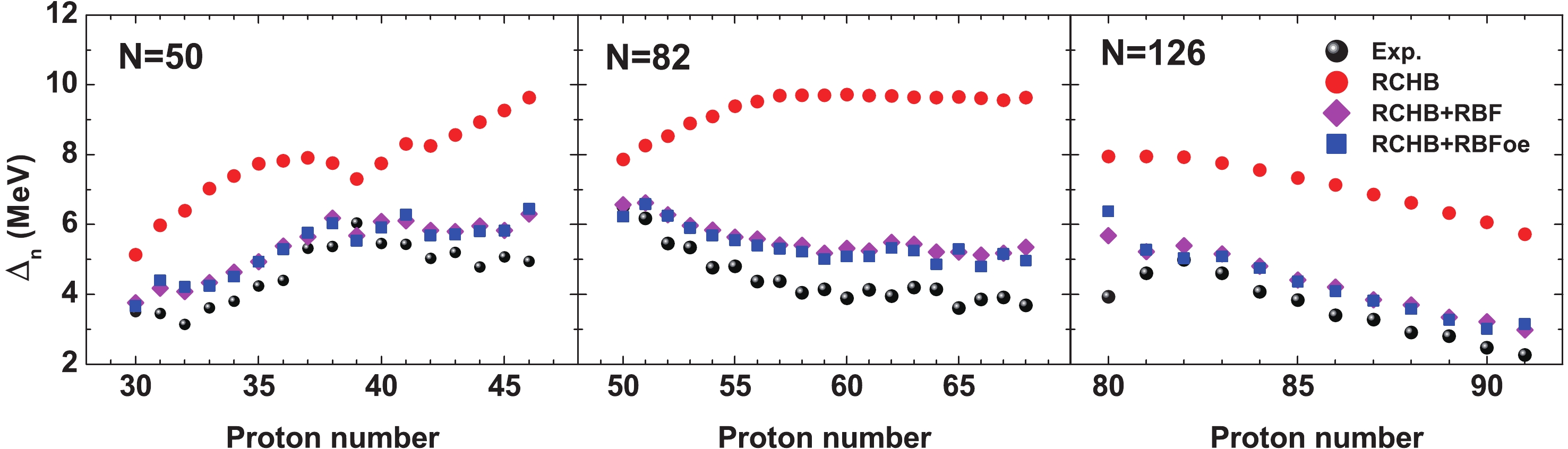
Figure 5. (color online) Neutron shell gap
$ \Delta_{n}(Z,A) $ =$ S_{2n}(Z,A)-S_{2n}(Z,A+2) $ for N = 50, N = 82, and N = 126 isotonic chains in the RCHB, RCHB+RBF and RCHB+RBFoe models. The experimental data are also shown for comparison.Although the improvement of the shell gap is negligible with RBFoe, it can improve the pairing effect significantly, as shown in Fig. 3. The single-nucleon separation energy is an important indicator of the pairing effect. The difference of the single-neutron separation energy between the experimental data and the predictions of the RCHB, RCHB+RBF, and RCHB+RBFoe models is presented in Fig. 6. In comparison with the results in Fig. 6(a), one can see that the systematic deviation of
$ S_{n} $ can be reduced in some regions by the RBF approach, as shown in Fig. 6(b).$ S_{n} $ for the RCHB+RBF model still shows large deviation with respect to the experimental data. In particular,$ \Delta S_n $ shows remarkable odd-even staggering (positive and negative$ \Delta S_n $ appear alternatively) in many regions. With RBFoe, the deviation of$ S_{n} $ is further reduced, and$ \sigma_{\rm{rms}} $ of$ S_{n} $ decreases from 0.581 MeV to 0.294 MeV. In addition, the odd-even staggering of$ \Delta S_n $ in the RCHB+RBF model is also removed by RBFoe, as shown in Fig. 6(c).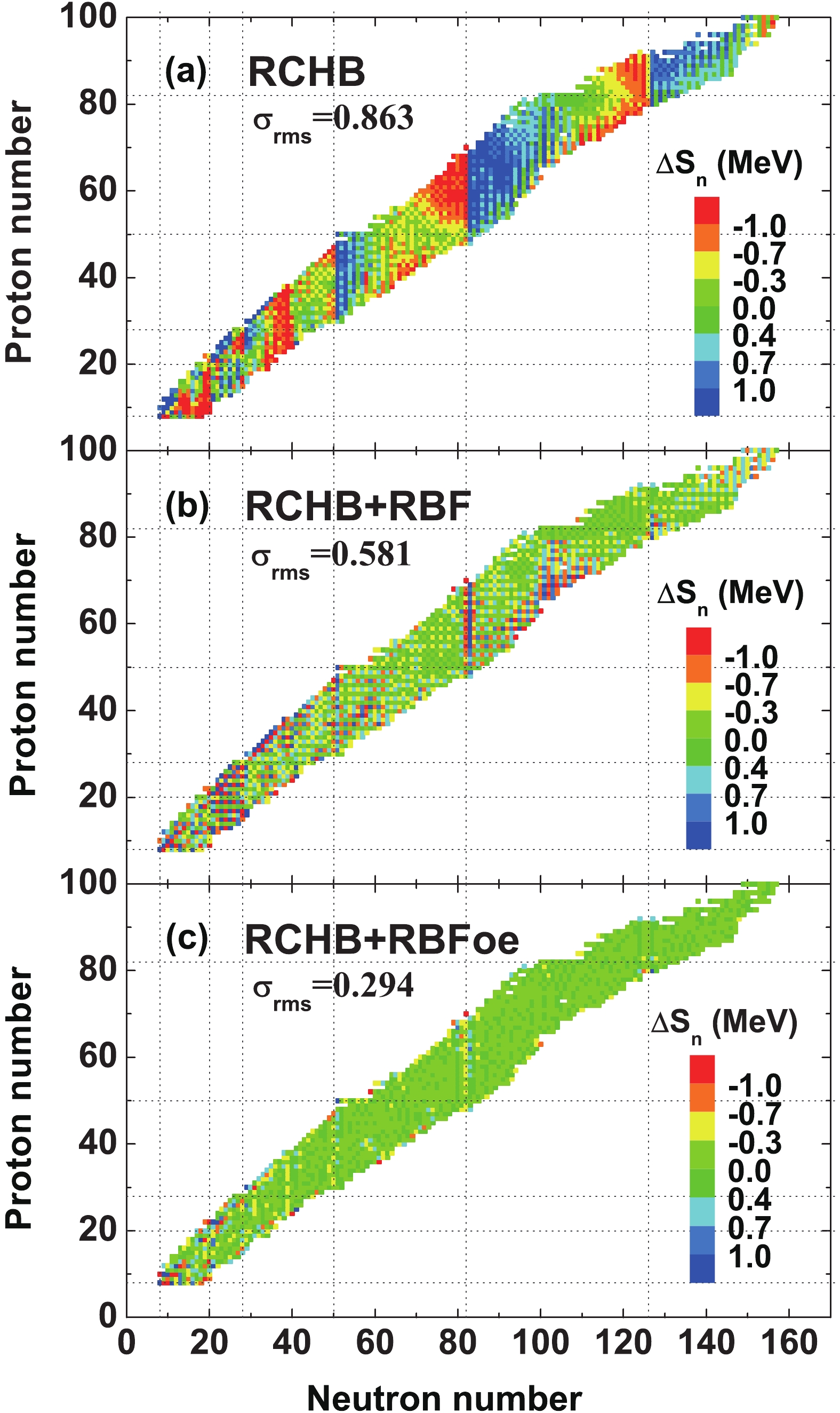
Figure 6. (color online) Same as Fig. 3, but for the single-neutron separation energy
$ S_{n} $ .It is also interesting to investigate the rms deviation of nuclear masses from different nuclear models as a function of the experimental value of
$ S_{n} $ [76], and the results for neutron-rich nuclei are shown in Fig. 7.$ \sigma_{\rm{rms}} $ of the RCHB model is significantly reduced by the RBF and RBFoe approaches not only for nuclei around the stability line with larger$ S_n $ , but also for very neutron-rich nuclei with smaller$ S_n $ . The accuracy is even better than of the HFB-31 and WS4 models. For neutron-deficient nuclei, the rms deviation is shown in Fig. 8 as a function of the experimental value of$ S_{p} $ [76]. Clearly, the RBFoe approach also improves the description of nuclear masses for neutron-deficient nuclei, and even for nuclei with small$ S_p $ .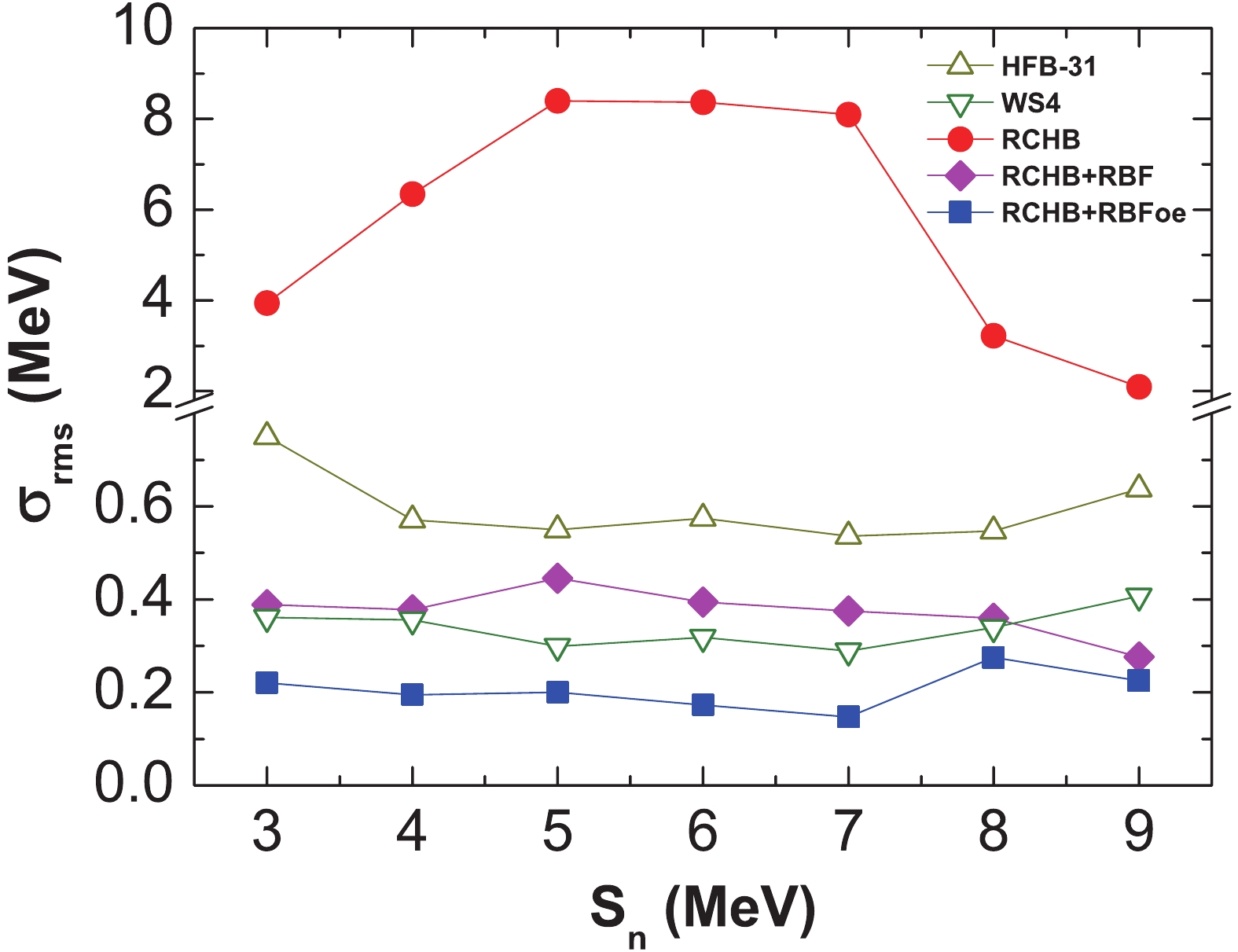
Figure 7. (color online) rms deviation
$\sigma_{\rm{rms}}$ of nuclear masses from different models with respect to the experimental data as a function of the experimental single-neutron separation energy$S_{n}$ for neutron-rich nuclei. The point at$S_{n}=x_{0}$ represents$\sigma_{\rm{rms}}$ for nuclei with$x_{0}\leqslant S_{n}<x_{0}+1$ . The experimental data are taken from AME16 [76].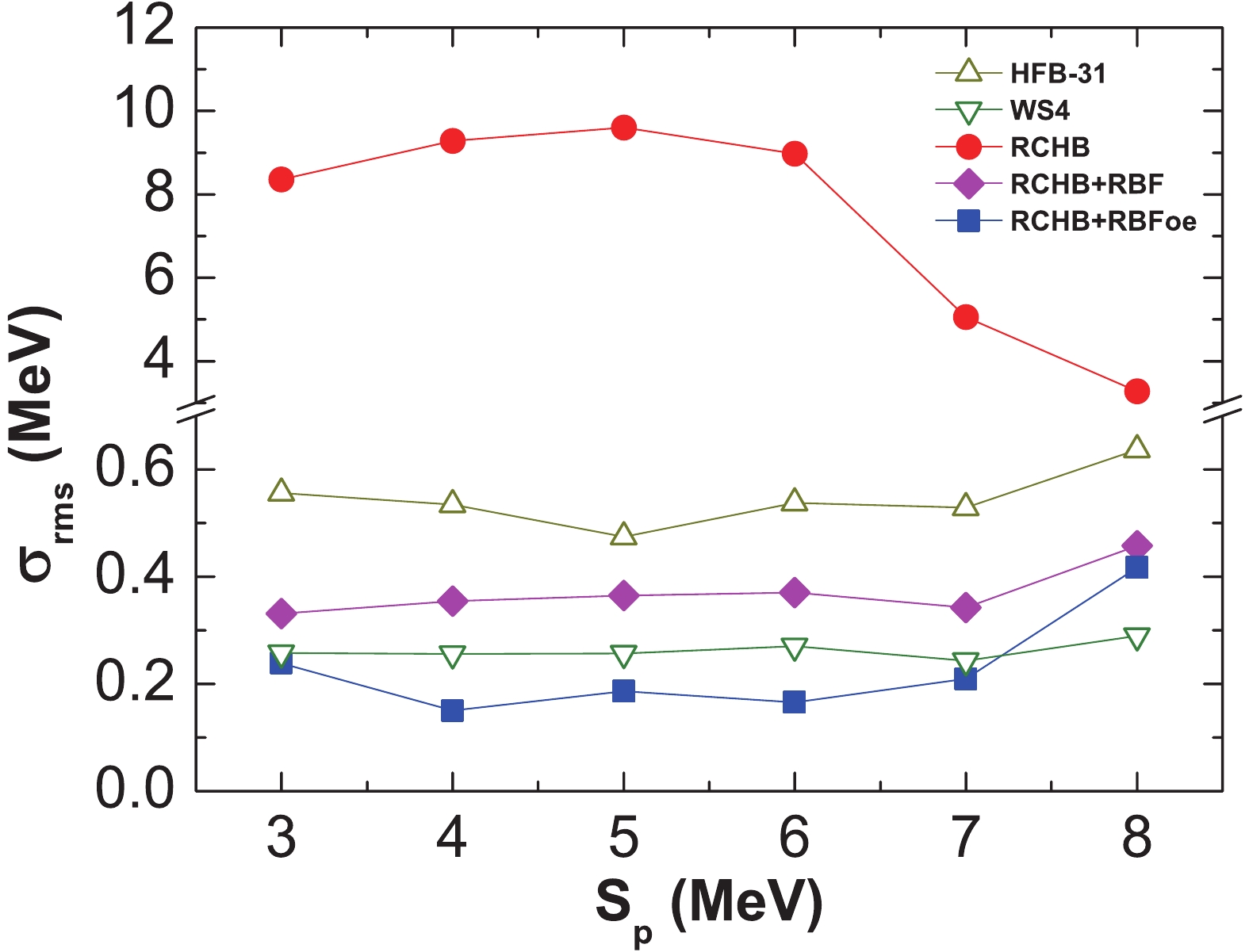
Figure 8. (color online) Same as Fig. 7, but for neutron-deficient nuclei as a function of single-proton separation energy
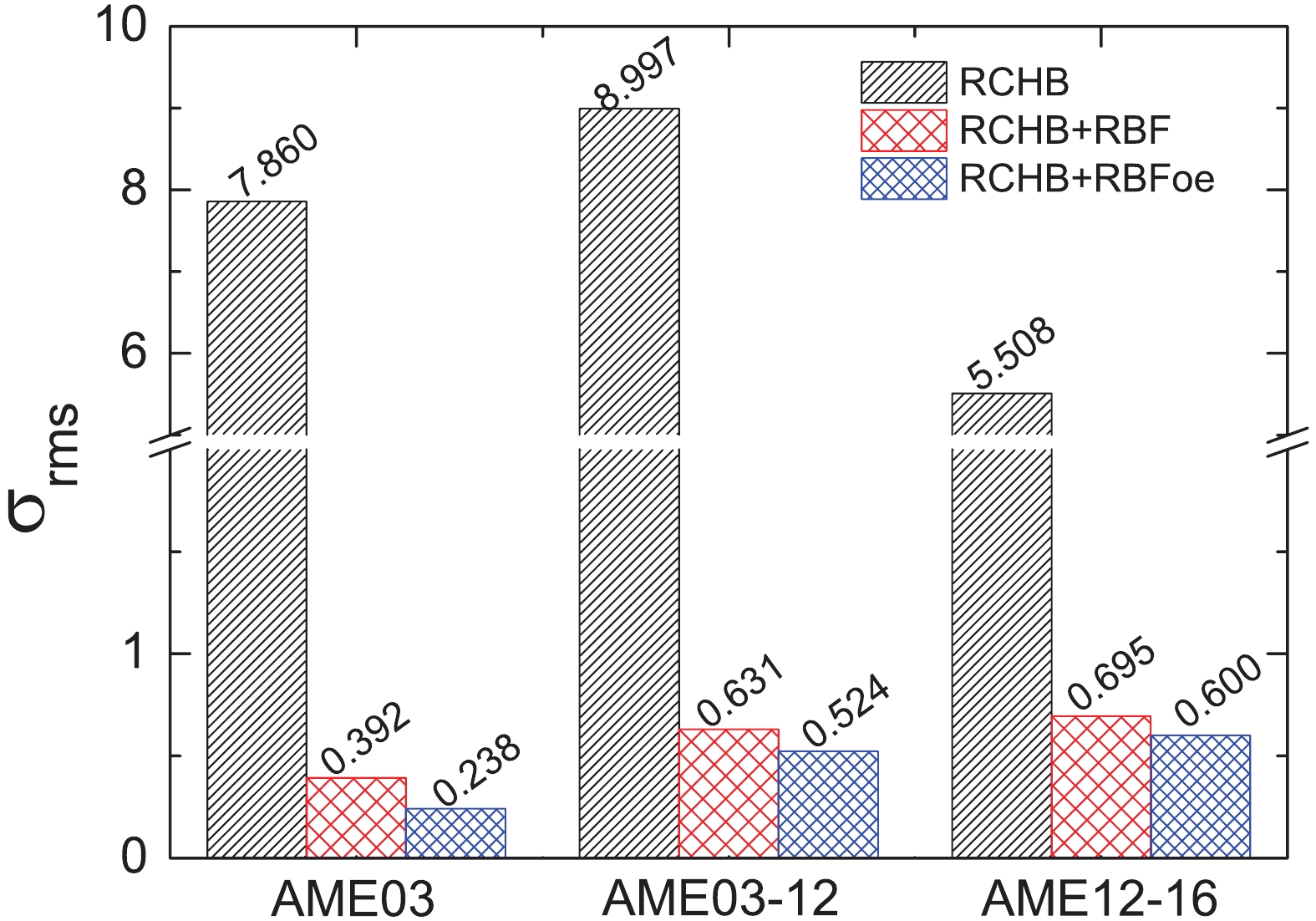
$S_{p}$ .In order to study the extrapolation ability of the RBF and RBFoe approaches, only nuclei appearing in AME03 are used as the training set, and nuclei appearing in AME12 (AME03-12) and AME16 (AME12-16) are used as the two testing sets. In Fig. 9,
$ \sigma_{\rm{rms}} $ of the mass predictions of RCHB, RCHB+RBF and RCHB+RBFoe are shown with respect to the experimental data from sets AME03, AME03-12 and AME12-16. There are 2096, 189 and 42 nuclei used for calculating the rms values in sets AME03, AME03-12 and AME12-16, respectively. Compared with the set AME03, used for rms deviation training, the rms deviations of RCHB+RBF and RCHB+RBFoe are only slightly larger for sets AME03-12 and AME12-16, while they are still much smaller than for the RCHB model. This indicates that both RBF and RBFoe approaches have a good extrapolation ability, at least in a region not far from the known nuclei. -
In this work, the RBF approach was employed to improve the mass predictions of the RCHB model. By including RBF, the local systematic deviations between mass predictions of the RCHB model and the experimental data are reduced significantly, and the rms deviation of the nuclear chart is reduced from 7.923 MeV to 0.386 MeV. However, the remaining mass difference shows clear odd-even staggering, which can be further reduced by the RBFoe approach, so that
$ \sigma_{\rm{rms}} $ decreases from 0.386 MeV to 0.229 MeV. Furthermore, our investigation showed that the neglected deformation effect in RCHB can be removed by both the RBF and RBFoe approaches. It was also found that the overestimated shell gap in the RCHB model can be improved by RBF, while RBFoe has an important effect on the description of the nucleon-separation energy, which is another important physical quantity for testing the accuracy of nuclear models. Recently, the BNN approach was also employed to improve the mass predictions of various nuclear models [72, 73, 75]. Therefore, it would be interesting to compare the predictive power of the RBF and BNN approaches for nuclear mass predictions in a future work.
Mass predictions of the relativistic continuum Hartree-Bogoliubov model with radial basis function approach
- Received Date: 2019-01-10
- Accepted Date: 2019-04-08
- Available Online: 2019-07-01
Abstract: The radial basis function (RBF) approach is a powerful tool to improve nuclear mass predictions. By combining the RBF approach with the latest relativistic continuum Hartree-Bogoliubov (RCHB) model, the local systematic deviations between the RCHB mass predictions and the experimental data are eliminated, and the root-mean-square (rms) mass deviation is significantly reduced from 7.923 MeV to 0.386 MeV. However, systematic deviations between the RBF improved mass predictions and the experimental data remain for nuclei with four different odd-even parities, i.e. (even Z, even N), (even Z, odd N), (odd Z, even N), and (odd Z, odd N). They can be reduced by separately training RBF for the four groups of nuclei, and the resulting rms deviation decreases to 0.229 MeV. It is found that the RBF approach can describe the deformation effects neglected in the present RCHB mass calculations, and also improves the description of the shell effect and the pairing effect.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: