Abstract
HTML
Reference
Related
PDF
-
Although the Heavy Quark Effective Theory (HQET) [1, 2, 3, 4] has achieved great success in the past decades in explaining and predicting the spectrum of charmed-strange mesons (
Ds ), there still exist discrepancies between the theoretical predictions and experimental measurements, especially for theP -wave excited states. The unexpectedly low masses ofD∗s0(2317)− andDs1(2460)− stimulated theoretical and experimental interest not only in them, but also in the other twoP -wave charmed-strange states,Ds1(2536)− andDs2(2573)− . The resonance parameters of theDs1(2536)− andD∗s2(2573)− mesons need more experimentally independent measurements [5]. In particular, the latest result on theD∗s2(2573)− mass from LHCb [6, 7] deviates from the other measurements [8, 9, 10] significantly, therefore the world average fit gives a bad qualityχ2/ndf=17.1/4 [5], wherendf is the number of degrees of freedom. In addition, the quantum numbers spin and parity (JP ) of theD∗s2(2573)− meson have been determined to beJP=2+ only recently with a partial wave analysis carried out by LHCb [11], and confirmation is needed.In recent years, measurements of the exclusive cross sections for
e+e− annihilation into charmed or charmed-strange mesons above the open charm threshold have attracted great interest. First, the charmonium states above the open charm threshold (ψ states) still lack of adequate experimental measurements and theoretical explanations. The latest parameter values of theseψ resonances are given by BES [12] from a fit to the total cross section of hadron production ine+e− annihilation. However, model predictions forψ decays into two-body final states were used, hence the values of the resonance parameters remain model-dependent. Studies of the exclusivee+e− cross sections would help to measure the parameters of theψ states model-independently. Second, many additionalY states withJP=1−− lying above the open charm threshold have been discovered recently [13-17]. Exclusive cross section measurements will provide important information in explaining these states. Measurements ofe+e− cross sections for theD(∗)(s)¯D(∗)(s) final states were performed by Belle [18-23], BABAR [24-26], and CLEO [27], only with low-lying charmed or charmed-strange mesons in the final states. Up to now, only theD¯D∗2(2460) final states ine+e− annihilation have been observed by Belle [28], others with higher excited charmed or charmed-strange mesons have not yet been observed. In addition, the cross sections ofe+e−→D¯D(∗)π have also been measured by CLEO [27] and BESIII [29-32]. However, a search for final states with strange flavor,e+e−→D+s¯D(∗)0K− , has not been performed before.Using
e+e− collision data corresponding to an integrated luminosity of 567pb−1 [33] collected at a center-of-mass energy of√s=4.600 GeV [34] with the BESIII detector operating at the Beijing Electron-Positron Collider (BEPCII), we observe the processese+e−→D+s¯D∗0K− ande+e−→D+s¯D0K− , which are found to be dominated byD+sDs1(2536)− andD+sD∗s2(2573)− , respectively. For the observedDs1(2536)− andD∗s2(2573)− mesons, we present the resonance parameters and determine the spin and parity ofD∗s2(2573)− . In addition, the processese+e−→ D+s¯D(∗)0K− are searched for using the data samples taken at four (two) center-of-mass energies between 4.416 (4.527) and 4.575 GeV, and upper limits at 90% confidence level on the cross sections are determined. Throughout the paper, the charge conjugate processes are implied to be included, unless explicitly stated otherwise. -
The BESIII detector is a magnetic spectrometer [35] located at the Beijing Electron Positron Collider (BEPCII) [36]. The cylindrical core of the BESIII detector consists of a helium-based multilayer drift chamber (MDC), a plastic scintillator time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), which are all enclosed in a superconducting solenoidal magnet providing a 1.0 T magnetic field. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identifier modules interleaved with steel. The acceptance for charged particles and photons is 93% over
4π solid angle. The charged-particle momentum resolution at 1 GeV/c is 0.5%, and the specific energy loss (dE/dx ) resolution is 6% for electrons from Bhabha scattering. The EMC measures photon energies with a resolution of 2.5%(5%) at 1 GeV in the barrel (end cap) region. The time resolution of the TOF barrel part is 68 ps, while that of the end cap part is 110 ps.Simulated data samples are produced with the GEANT4-based [37] Monte Carlo (MC) package which includes the geometric description of the BESIII detector and the detector response. They are used to determine the detection efficiency and to estimate the backgrounds. The simulation includes the beam energy spread and effects of initial state radiation (ISR) in the
e+e− annihilations modeled with the generator KKMC [38]. The inclusive MC samples consist of the production of open charm processes, the ISR production of vector charmonium(-like) states, and the continuum processes incorporated in KKMC [38]. The known decay modes are modeled with EVTGEN [39] using branching fractions taken from the Particle Data Group [5], and the remaining unknown decays from the charmonium states with LUNDCHARM [40]. Final state radiation (FSR) from charged final state particles is simulated with the PHOTOS package [41]. The intermediate states in theD+s→K+K−π+ decay are considered in the simulation [42]. In the measurements ofDs1(2536)− andD∗s2(2573)− resonance parameters, the angular distributions are taken into account in the generation of signal MC samples. For the signal process ofe+e−→D+sDs1(2536)−,Ds1(2536)−→¯D∗0K− , the spin-parity of theDs1(2536)− meson is assumed to be1+ . To determine the spin-parity ofD∗s2(2573)− , efficiencies were obtained from the two MC samples, which assume the spin-parity as1− or2+ . The MC sample with spin-parity2+ is used in the measurement of theD∗s2(2573)− resonance parameters. -
To identify the final state
D+s¯D(∗)0K− , a partial reconstruction method is adopted, in which we detect theK− and reconstructD+s candidates through theD+s→K+K−π+ decay. The remaining¯D(∗)0 meson is identified with the mass recoiling against the reconstructedK−D+s system.For each of the four reconstructed charged tracks, the polar angle in the MDC must satisfy
|cosθ|<0.93 , and the distance of the closest approach from thee+e− interaction point to the reconstructed track is required to be within10 cm in the beam direction and within1 cm in the plane perpendicular to the beam direction. The ionization energy lossdE/dx measured in the MDC and the time of flight measured by the TOF are used to perform the particle identification (PID). Pion candidates are required to satisfyprob(π)>prob(K) , whereprob(π) andprob(K) are the PID confidence levels for a track to be a pion and kaon, respectively. Kaon candidates are identified by requiringprob(K)>prob(π) .The
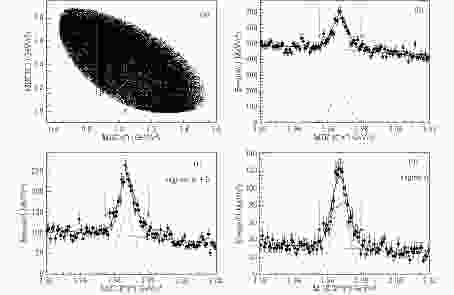
D+s meson candidates are reconstructed from two kaons with opposite charge and one charged pion. To satisfy strangeness and charge conservation, eachD+s candidate must be accompanied by a negatively charged kaon. For theD+s candidates, the distributions of the reconstructed massesM(K+K−) versusM(K−π+) andM(K−K+π+) are shown in Figs. 1(a) and (b), respectively. The two dominant sub-resonant decays, i.e., a horizontal band for the processD+s→ϕπ+ and a vertical band for the processD+s→K+¯K∗(892)0 are clearly visible. To improve the signal significance in Fig. 1(b), only theD+s candidates which satisfyM(K+K−)<1.05GeV/c2 (region A) or0.863<M(K−π+)<0.930GeV/c2 (region B) are retained. The correspondingM(K−K+π+) distributions for events in region A+B and A are plotted in Figs. 1(c) and (d), respectively, showing improved signal significance. The finalD+s candidates must have a reconstructed massM(K−K+π+) in the region(1.955,1.980)GeV/c2 .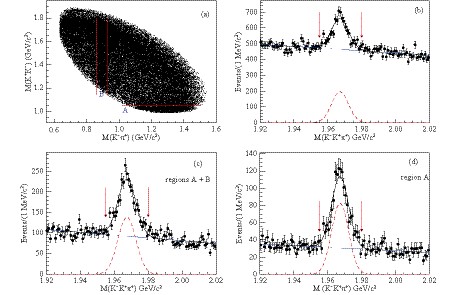
Figure 1. (color online) Scatter plot of
M(K+K−) versusM(K−π+) for theD+s→K+K−π+ candidates (a) and the corresponding invariant massM(K+K−π+) distribution (b) for data at√s=4.600 GeV. TheM(K+K−π+) distributions of the subsamples from the regions A+B and from the region A are shown in plot (c) and (d), respectively. In plots (b), (c) and (d), fits with the sum of a Gaussian function and a first-order polynomial function are implemented to determine the signal regions for theD+s candidates. The signal windows are shown with arrows.In this analysis, the resolution of the recoiling mass is improved by using the variables
RQ(K−D+s)≡RM(K−D+s)+ M(D+s)−m(D+s) andRQ(D+s)≡RM(D+s)+M(D+s)−m(D+s) . Here,RM(D+s) andRM(K−D+s) are the reconstructed recoiling masses against theD+s andK−D+s system, respectively,M(D+s) is the reconstructedD+s mass andm(D+s) is the nominalD+s mass taken from the world average [5]. -
To reject the backgrounds from
Λ+c decays in the measurement of the cross section ofe+e−→D+s¯D(∗)0K− , we further demand thatRQ(D+s)<2.59GeV/c2 . Figure 2 presents evident peaks in the distribution ofRQ(K−D+s) around the signal positions of¯D∗0 and¯D0 , which correspond to the processese+e−→D+s¯D∗0K− andD+s¯D0K− , respectively.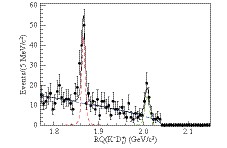
Figure 2. (color online) Distributions of
RQ(K−D+s) for theD+s signal candidates in regions A+B in Fig. 1(c), for data taken at√s=4.600 GeV. The solid line shows the total fit to the data points and the dashed lines represent the¯D0 and¯D∗0 signals.To determine the signal yields of the processes
e+e−→D+s¯D(∗)0K− at 4.600 GeV, an unbinned maximum likelihood fit is performed to theRQ(K−D+s) spectrum as shown in Fig. 2. The signal peaks are described by the MC-determined signal shapes and the background shape is taken as an ARGUS function [43]. In the fit to data, the endpoint of the background shape is fixed at the value obtained from a fit of an ARGUS function to theRQ(K−D+s) spectrum in the background MC sample. The Born cross section is calculated asσB=NobsL(1+δ)1|1−Π|2Bϵ,
(1) where
Nobs is the number of the observed signal candidates,L is the integrated luminosity,ϵ is the detection efficiency determined from MC simulations,(1+δ) is the radiative correction factor [44],1|1−Π|2 is the vacuum polarization factor [45], andB is branching fraction ofD+s→K+K−π+ . The detection efficiencies are estimated based on MC simulations, assuming the two-body final states ofD+sDs1(2536)− andD+sD∗s2(2573)− dominate the decays toD+s¯D(∗)0K− according to the studies in Secs. 4.2 and 4.3. The numerical results are given in Table 1.√s /GeV
4.600 4.575 4.527 4.467 4.416 L(pb−1) 
567 48 110 110 1029 1|1−Π|2 
1.059 1.059 1.059 1.061 1.055 1+δ 
0.765 0.755 0.735 ϵ (%)
16.1 14.3 13.2 D+s¯D∗0K− 
Nobs 
41.0±9.3 
0.0+2.0−0.0 
2.3+3.9−2.3 
σB (pb)
10.1±2.3±0.8 
0.0+7.3+1.1−0.0−0.0 
3.9+6.6−3.9±0.4 
Nup 
3.7 6.7 σBU.L. (pb)
13.5 11.3 1+δ 
0.694 0.698 0.702 0.691 0.762 ϵ (%)
22.3 23.9 20.3 18.2 14.6 D+s¯D0K− 
Nobs 
98.4±11.7 
0.0+3.0−0.0 
1.7+4.5−1.7 
4.1+7.1−4.1 
1.2+8.0−1.2 
σB (pb)
19.4±2.3±1.6 
0.0+6.5+0.9−0.0−0.0 
1.9+5.0−1.9±0.2 
5.1+8.9−5.1±0.4 
0.3+1.2−0.3±0.1 
Nup 
5.8 7.3 10.6 10.5 σBU.L. (pb)
12.7 8.1 13.2 1.6 Table 1. Cross section measurements at different energy points. For the cross sections, the first set of uncertainties are statistical and the second are systematic. The uncertainties of the number of observed signals are statistical only. The four samples with lower center-of-mass energies suffer from low statistics, we therefore set the lower and upper boundary of the uncertainties of Nobs as 0 and the upper limits at the 68.3% confidence level, respectively.
-
For the candidates surviving the basic event selections, we further select the signal candidates for
e+e−→D+s¯D∗0K− by requiring1.993<RQ(K−D+s)< 2.024GeV/c2 , as shown in Fig. 3(a). TheRQ(D+s) distribution of the remaining events is displayed in Fig. 4(a), where a clearDs1(2536)− signal peak near the nominalDs1(2536)− mass is visible. An unbinned maximum likelihood fit is performed to the distribution, where the signal shape is taken as a sum of the efficiency-weighted D-wave and S-wave Breit-Wigner functions convolved with the detector resolution function,[E⋅(f⋅BWS+(1−f)⋅ BWD)]⊗R . Here, the resolution functionR (plotted in Fig. 4(c)) and the efficiencyE (plotted in Fig. 4(b)) are determined from MC simulations, andf is the fraction of theS -wave Breit-Wigner function. The S-wave and D-wave Breit-Wigner functions are BWS =1(RQ2−m2)2+m2Γ2⋅p⋅q , andBWD=1(RQ2−m2)2+m2Γ2⋅ p5⋅q , respectively, where m andΓ are the mass and width of theDs1(2536)− to be determined andp(q) is the momentum ofK− (D+s ) in the rest frame ofK−¯D∗0 (e+e− ) system. The backgrounds are described with a first-order polynomial function. The parameterf is fixed to 0.72 [46], while the other parameters are determined in the fit.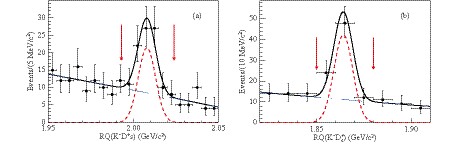
Figure 3. (color online) At 4.600 GeV, (a) the
RQ(K−D+s) distribution for theD+s candidates from signal regions A and B in Fig. 1(c); (b) theRQ(K−D+s) distribution for theD+s candidates from signal regions A in Fig. 1(d). Fits with the sum of a Gaussian function and a first-order polynomial function are implemented to determine the signal regions for the¯D(∗)0 candidates, which are indicated with arrows.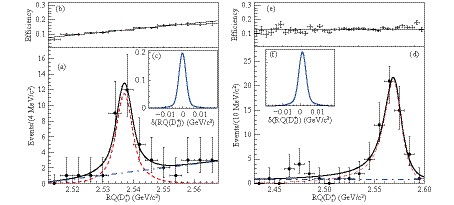
Figure 4. (color online) At 4.600 GeV, the
RQ(D+s) spectra in the samples ofe+e−→D+s¯D∗0K− (left) ande+e−→D+s¯D0K− (right). Plots (a) and (d) show the result of the unbinned maximum likelihood fits. Data are denoted by the dots with error bars. The dash-dotted and dotted lines are the background and signal contributions, respectively. Plots (b) and (e) show the efficiency functions. Plots (c) and (f) show theRQ(D+s) resolution functions determined from MC simulations.In this fit, the number of signal candidates is estimated to be
24.0±5.7(stat) . The mass and width of theDs1(2536)− are measured to be(2537.7±0.5(stat)± 3.1(syst))MeV/c2 , and(1.7±1.2(stat)±0.6(syst))MeV , respectively. The branching fraction weighted Born cross section is determined to beσB(e+e−→D+sDs1(2536)−+c.c.)⋅ B(Ds1(2536)−→¯D∗0K−)=(7.5±1.8±0.7) pb. The relevant systematic uncertainties are discussed later and summarized in Table 3.σB(e+e−→D+s¯D(∗)0K−) at different
√s /GeV
e+e−→D+sD−sJ at 4.600 GeV
source 4.600 4.575 4.527 4.467 4.416 Ds1(2536)− 
D∗s2(2573)− 
tracking 4 4 4 4 4 4 4 particle ID 4 4 4 4 4 4 4 luminosity 1 1 1 1 1 1 1 branching faction 3 3 3 3 3 3 3 center-of-mass energy ⋯ 
⋯ 
⋯ 
⋯ 
⋯ 
⋯ 
⋯ 
fit range ( ⋯ , 2)
(2, ⋯ )
(4, 3) ( ⋯ , -)
( ⋯ , -)
3 4 background shape (3, 1) (1, 4) (4, 5) (5, -) (6, -) 4 5 line shape (3, 4) (2, 3) (1, 1) (1, -) ( ⋯ , -)
4 3 total: (8, 8) (7, 8) (9, 9) (8, -) (9, -) 9 10 Table 3. Relative systematic uncertainties (in %) on the cross section measurement. The first value in brackets is for
D+s¯D0K− , and the second forD+s¯D∗0K− . “⋯ ” means the uncertainty is negligible. “-” means unavailable due to√s being below the production threshold. -
To study the
D∗s2(2573)− properties, we select the signal candidates of the processe+e−→D+s¯D0K− by requiringRQ(K−D+s) in the¯D0 signal region of(1.850,1.880)GeV/c2 , as shown in Fig. 3(b). To avoid affecting theRQ(D+s) distribution, the forementioned requirementRQ(D+s)<2.59Gev/c2 is not applied here, and only theD+s candldates in region A of Fig. 1 are used. For the selected events, the correspondingRQ(D+s) distribution is plotted in Fig. 4(d), where a clearD∗s2(2573)− signal peak near the knownD∗s2(2573)− mass is observed.An unbinned maximum likelihood fit is performed to the
RQ(D+s) spectrum in Fig. 4(d). The spin-parity of theD∗s2(2573)− meson is fixed to be2+ , following the studies in Sec. 4.4, and theD∗s2(2573)− meson is assumed to decay to¯D0K− predominantly viaD -wave [2]. Hence, we take the D-wave Breit-Wigner functionBW=1(RQ2−m2)2+m2Γ2⋅p5⋅q5 convolved with the resolution function (shown in Fig. 4(f)),BW⊗R , to describe the signal, and a constant to represent backgrounds. Here,p(q) is the momentum ofK− (D+s ) in the rest frame of theK−¯D0 (e+e− ) system. Figure 4 (e) shows the efficiency distribution with the assignmentJP=2+ , which is consistent with a flat line. All parameters are left free in the fit.The fit yields
61.9±9.1(stat) signal events. The mass and width of theD∗s2(2573)− are measured to be(2570.7±2.0(stat)±1.7(syst))MeV/c2 , and(17.2± 3.6(stat)±1.1(syst))MeV , respectively, where the systematic uncertainties are summarized in Table 2. The branching fraction weighted Born cross section is given to beσB(e+e−→D+sD∗s2(2573)−+c.c.)⋅B(D∗s2(2573)−→¯D0K−)= (19.7±2.9±2.0) pb. The relevant systematic uncertainties are discussed later and summarized in Table 3.mass /(MeV/c2) width/MeV source Ds1(2536)− 
D∗s2(2573)− 
Ds1(2536)− 
D∗s2(2573)− 
mass shift 3.0 1.3 ⋯ 
⋯ 
detector resolution ⋯ 
⋯ 
0.5 0.1 center-of-mass energy 0.7 1.0 0.2 0.3 signal model ⋯ 
⋯ 
background shape 0.2 0.4 0.2 0.3 fit range ⋯ 
⋯ 
0.2 1.0 total 3.1 1.7 0.6 1.1 Table 2. Summary of systematic uncertainties on the
Ds1(2536)− andD∗s2(2573)− resonance parameters measured at√s=4.600 GeV. “⋯ ” means the uncertainty is negligible. -
At
√s=4.600 GeV, the exclusive processe+e−→D+sD∗s2(2573)−→D+s¯D0K− is observed right above the production threshold. For theD∗s2(2573)− meson, theJP assignments with high spins would be strongly suppressed in this process. Hence, we assume that theD∗s2(2573)− meson can only have two possibleJP assignments,1− or2+ . Under these two hypotheses, the differential decay rates as a function of the helicity angleθ′ of theK− in the rest frame of theD∗s2(2573)− ,dN/dcosθ′ , follow two very distinctive formulae of(1−cos2θ′) for1− andcos2θ′(1−cos2θ′) for2+ . We can determine the true spin-parity from tests of the two hypotheses based on data.In each
|cosθ′| interval of width 0.2, the number of background events is estimated from theRQ(D+s) sideband region (2.44, 2.50) GeV/c2 according to the global fit shown in Fig. 4 (d) and subtracted from the signal candidates in the signal region, (2.54, 2.60) GeV/c2 . Then we obtain the efficiency-corrected angular distribution ofdσ/d|cosθ′| , as depicted in Fig. 5 for theD∗s2(2573)− signals. The efficiency distributions in Figs. 5 (a) and (c)are obtained from the signal MC simulation samples, which assume the spin-parity of theD∗s2(2573)− as1− and2+ , respectively.
Figure 5. (color online) At 4.600 GeV, the efficiency-corrected
|cosθ′| distribution for the background-subtractedD∗s2(2573)− signals are shown in plots (b) and (d). Plots (a) and (c) are the corresponding efficiency distributions under theJP assumptions of1− and2+ , respectively. The shapes to be tested are shown in (b) and (d) for the two hypotheses, normalized to the area of data distribution.The shapes of the two spin-parity hypotheses are constructed as
a1(1−cos2θ′) anda2cos2θ′(1−cos2θ′) for1− and2+ , respectively. Here,a1 anda2 normalize the shapes to the area of the efficiency corrected angular distributions. To test the two different assumptions, we calculateχ2=Σ(yi−μiσi)2 , wherei is the index of the interval in the angular distributions,yi is the estimated signal yield in intervali ,σi is the corresponding statistical uncertainty, andμi is the expected number of signal events. The values ofχ2 for theJP=1− and2+ assumptions are evaluated as278.67 and7.85 , respectively. Hence, combined with the result from LHCb [11], our results strongly favor theJP=2+ assignment and rule out theJP=1− assignment for theD∗s2(2573)− . -
The process
e+e−→D+s¯D(∗)0K− is also searched for at four (two) other energy points. The corresponding integrated luminosities [33] and center-of-mass energies [34] are shown in Table 1. The analysis strategy and event selection are the same as those explained in Sec. 3. The resultantRQ(K−D+s) distributions are shown in Fig. 6, together with the results of unbinned maximum likelihood fits as described in Sec. 4.1. The fit results are given in Table 1.
Figure 6. (color online)
RQ(K−D+s) distributions and the fit results at each energy point. Points with error bars are data, the dotted lines peaking at the nominal mass of the¯D0 (¯D∗0 ) are the signal shapes fore+e−→D+s¯D0K−(D+s¯D∗0K−) process.As has been studied with the largest statistics data at
√s=4.600 GeV, the processesD+sDs1(2536)− andD+sD∗s2(2573)− dominate the processese+e−→D+s¯D∗0K− ande+e−→D+s¯D0K− , respectively. We assume that this conclusion still holds for the MC simulations of the final states ofD+s¯D(∗)0K− for the energy points above theD+sDs1(2536)− orD+sD∗s2(2573)− mass thresholds. For the energy points below the mass thresholds, the signal MC simulation samples of the three-body processes are generated with average momentum distributions in the phase space.Since the four data samples taken at lower energies suffer from low statistics, we also present upper limits at the 90% confidence level on the cross sections. The upper limits are determined using a Bayesian approach with a flat prior. The systematic uncertainties are considered by convolving the likelihood distribution with a Gaussian function representing the systematic uncertainties. The numerical results are summarized in Table 1.
-
The systematic uncertainties on the resonance parameters and cross section measurements are summarized in Tables 2 and 3, respectively, where the total systematic uncertainties are obtained by adding all items in quadrature. For each item, details are elaborated as follows.
1. Tracking efficiency. The difference in tracking efficiency for the kaon and pion reconstruction between the MC simulation and the real data is estimated to be 1.0% per track [47]. Hence, 4.0% is taken as the systematic uncertainty for four charged tracks.
2. PID efficiency. The uncertainty of identifying the particle types of kaon and pion is estimated to be 1% per charged track [47]. Therefore, 4.0% is taken as the systematic uncertainty for the PID efficiency of the four detected charged tracks.
3. Signal Model. In the fits of the
Ds1(2536)− , the fraction of theD -wave andS -wave components is varied according to the Belle measurement [46], and the maximum changes on the fit results are taken as systematic uncertainties. In the measurement of theD∗s2(2573)− resonance parameters, the uncertainty stemming from the signal model is negligible as theD -wave amplitude dominates in the heavy quark limit.4. Background Shape. In the measurements of the
Ds1(2536)− andD∗s2(2573)− resonance parameters, linear background functions are used in the nominal fits. To estimate the uncertainties due to the background parametrization, higher order polynomial functions are studied, and the largest changes on the final results are taken as the systematic uncertainty. In the measurement ofσB(e+e−→D+s¯D(∗)0K− ), we replace the ARGUS background shape in the nominal fit with a second-order polynomial functiona(m−m0)2+b , wherem0 is the threshold value and is the same as that in the nominal fit, whilea andb are free parameters. We take the difference on the final results as the systematic uncertainty.5. Fit Range. We vary the boundaries of the fit ranges to estimate the relevant systematic uncertainty, which are taken as the maximum changes on the numerical results.
6. Mass Shift and Detector Resolution. In the nominal fits to measure the
Ds1(2536)− andD∗s2(2573)− resonance parameters, the effects of a mass shift and the detector resolution are included in the MC determined detector resolution shape. The potential bias from the MC simulations is studied using the control sample ofe+e−→D+sD∗−s . We select theD+s candidates following the aforementioned selection criteria and plot theRQ(D+s) distribution to be fitted to theD∗−s peak. The signal function is composed of a Breit-Wigner shape convolved with a Gaussian function. We extract the detector resolution parameters from a series of fits at different momentum intervals of theD+s candidates. Hence, the absolute resolution parameters for the fits to theDs1(2536)− orD∗s2(2573)− are extrapolated according to the detectedD+s momentum. In an alternative fit, we fix the resolution parameters according to this study, instead of to the MC-determined resolution shape. The resultant change in the new fit from the original fit is considered as the systematic uncertainty.7. Branching Fraction. The systematic uncertainty in the branching fraction for the process
D+s→K+K−π+ is taken from PDG [5].8. Luminosity. The integrated luminosity of each sample is measured with a precision of 1% with Bhabha scattering events [33].
9. Center-of-mass energy. We change the values of center-of-mass energy of each sample according to the uncertainties in Ref. [34] to estimate the systematic uncertainties due to the center-of-mass energy.
10. Line Shape of Cross Section. The line shape of the
e+e−→D+s¯D(∗)0K− cross section (including the intermediateDs1(2536)− andD∗s2(2573)− states) affects the radiative correction factor and the detection efficiency. This uncertainty is estimated by changing the input of the observed line shape to the simulation. In the nominal measurement, a power function ofc⋅(√s−E0)d is taken as the input of the observed line shape. Here,E0 is the production threshold energy for the processe+e−→D+s¯D(∗)0K− , andc andd are parameters determined from fits to the observed line shape. To estimate the uncertainty, we change the exponent of the nominal input power function tod±1 and compare the results with the nominal measurement. The largest difference is taken as the systematic uncertainty. -
We study the process
e+e−→D+s¯D(∗)0K− at 4.600 GeV and observe the twoP -wave charmed-strange mesons,Ds1(2536)− andD∗s2(2573)− . TheDs1(2536)− mass is measured to be(2537.7±0.5±3.1)MeV|/c2 and its width is(1.7±1.2±0.6) MeV, both consistent with the current world-average values in PDG [5]. The mass and width of theD∗s2(2573)− meson are measured to be(2570.7±2.0±1.7)MeV|/c2 and(17.2±3.6±1.1) MeV, respectively, which are compatible with the LHCb [6, 7] and PDG [5] values. The spin-parity of theD∗s2(2573)− meson is determined to beJP=2+ , which confirms the LHCb result [11]. The Born cross sections are measured to beσB(e+e−→D+s¯D∗0K−)=(10.1±2.3±0.8) pb andσB(e+e−→D+s¯D0K−)=(19.4±2.3±1.6) pb. The products of the Born cross sections and the decay branching fractions are measured to beσB(e+e−→D+sDs1(2536)− +c.c.)⋅ B(Ds1(2536)−→¯D∗0K−)=(7.5±1.8±0.7) pb andσB(e+e−→D+sD∗s2(2573)−+c.c.)⋅B(D∗s2(2573)−→¯D0K−)= (19.7±2.9±2.0) pb. In addition, the processese+e−→ D+s¯D(∗)0K− are searched for using small data samples taken at four (two) center-of-mass energies between 4.416 (4.527) and 4.575 GeV, and upper limits at the 90% confidence level on the cross sections are determined. -
The BESIII collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support.
Observation of
e+e−→D+s¯D(∗)0K−
and study of the P-wave
Ds
mesons
- Received Date: 2018-12-21
- Available Online: 2019-03-01
Abstract: Studies of
DownLoad: