-
In hadronic matter that is created in ultrarelativistic heavy-ion collisions, various types of meson-meson scatterings take place. The meson-meson scattering can be studied in quark degrees of freedom or meson degrees of freedom. Elastic
$\pi \pi$ scattering for$I=2$ and elastic$\pi K$ scattering for$I=3/2$ have been studied in the quark interchange mechanism in the first Born approximation [1-4] and in nonperturbative schemes along with the chiral perturbation theory [5-13]. The reactions$\pi \pi \to \rho \rho$ for$I=2$ ,$KK \to K^*K^*$ for$I=1$ ,$\pi K \to \rho K^*$ for$I=3/2$ , and so on have also been studied in the quark interchange mechanism [14, 15]. The reactions$\pi \pi \to K \bar K$ ,$\rho \rho \to K \bar K$ ,$\pi \rho \to K \bar {K}^*$ , and$\pi \rho \to K^* \bar {K}$ can be studied by quark-antiquark annihilation and creation in the first Born approximation [16] or through one-meson exchange in effective meson Lagrangians [17, 18]. Furthermore, the four isospin channels,$\pi K \to \rho K^\ast$ for$I=1/2$ ,$\pi K^\ast \to \rho K$ for$I=1/2$ ,$\pi K^\ast \to \rho K^\ast$ for$I=1/2$ , and$\rho K \to \rho K^\ast$ for$I=1/2$ , are studied under the assumption that quark interchange as well as quark-antiquark annihilation and creation are dominant mechanisms [19]. These studies have revealed interesting features of these reactions. For example, the cross section for the inelastic meson-meson scattering governed by quark interchange increases very rapidly and attains a maximum value; then, it decreases rapidly while the center-of-mass energy of the two colliding mesons increases from the threshold. However, the cross section for the inelastic meson-meson scattering governed by quark-antiquark annihilation and creation may decrease very slowly from the maximum value.In the present work, we are interested in the inelastic meson-meson scattering among
$\pi$ ,$\rho$ ,$K$ , and$K^\ast$ mesons, which is assumed to be dominated by quark-antiquark annihilation and creation. The meson-meson reactions studied in Ref. [16] include$\pi \pi \to \rho \rho$ ,$K \bar {K} \to K^* \bar {K}^\ast$ ,$K \bar{K}^\ast \to $ $ K^* \bar{K}^\ast$ ,$K^\ast \bar{K} \to K^* \bar{K}^\ast$ ,$\pi \pi \to K \bar K$ ,$\pi \rho \to K \bar {K}^\ast$ ,$\pi \rho \to K^* \bar{K}$ , and$K \bar {K} \to \rho \rho$ . However, these reactions do not exhaust all the 2-to-2 meson-meson reactions among$\pi$ ,$\rho$ ,$K$ , and$K^\ast$ mesons. Hence, in the present work, we study these reactions:$K \bar {K} \to K \bar {K}^\ast$ ,$K \bar{K} \to K^* \bar{K}$ ,$\pi K \to \pi K^\ast$ ,$\pi K \to \rho K$ ,$\pi \pi \to K \bar{K}^\ast$ ,$\pi \pi \to K^\ast \bar{K}$ ,$\pi \pi \to K^\ast \bar{K}^\ast$ ,$\pi \rho \to K \bar{K}$ ,$\pi \rho \to K^\ast \bar{K}^\ast$ ,$\rho \rho \to K^\ast \bar{K}^\ast$ ,$K \bar{K}^\ast \to \rho \rho$ , and$K^* \bar{K} \to \rho \rho$ . These reactions have not been studied elsewhere, and they complement the reactions studied in Ref. [16].The remainder of this paper is organized as follows. In Section 2, we present the formulae of unpolarized cross sections for 2-to-2 meson-meson reactions that are governed by the annihilation of a quark-antiquark pair and creation of another quark-antiquark pair. In Section 3, we calculate the transition amplitudes with mesonic quark-antiquark wave functions and the transition potential for quark-antiquark annihilation and creation. In Section 4, we show unpolarized cross sections for inelastic meson-meson scattering, and provide relevant discussions. In Section 5, we summarize the present work.
-
It is shown by the two Feynman diagrams in Fig. 1 that the reaction
$A+B \to C+D$ is caused by quark-antiquark annihilation and creation in the Born approximation. In the left diagram of Fig. 1, the quark of meson$A$ and the antiquark of meson$B$ annihilate into a gluon; this gluon creates a new quark-antiquark pair. The new quark and the antiquark in meson$A$ combine into meson$C$ and the new antiquark and the quark in meson$B$ combine into meson$D$ . In the right diagram of Fig. 1, the antiquark of meson$A$ and the quark of meson$B$ annihilate into a gluon. The gluon creates a new quark-qnatiquark pair, and the new antiquark and the quark of meson$A$ form meson$C$ , and the new quark and the antiquark of meson$B$ form meson$D$ . These are the processes that we consider in the present work.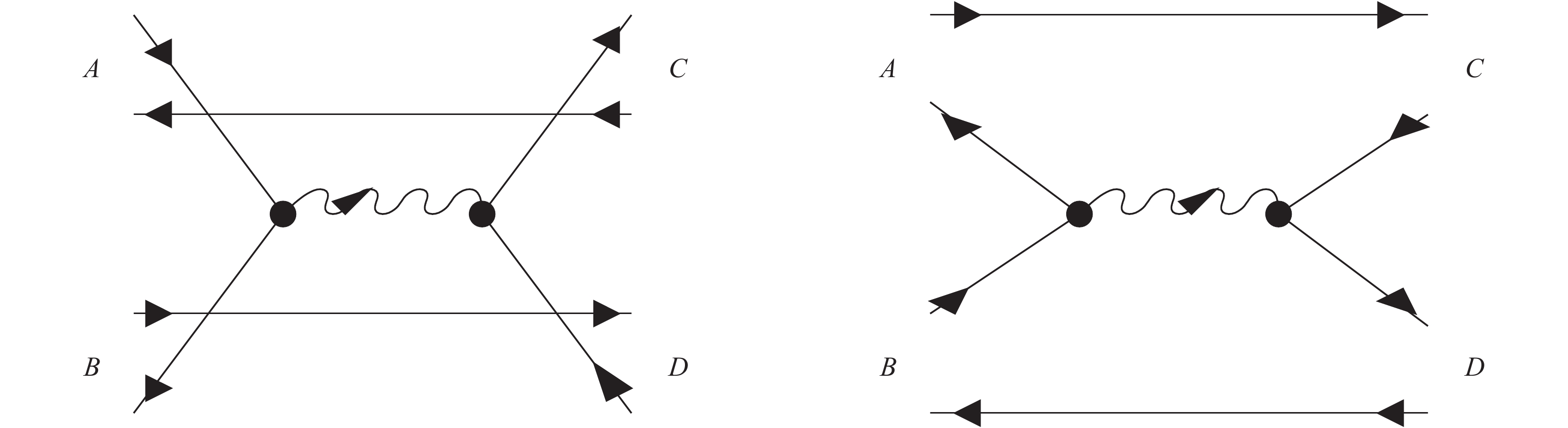
Figure 1. Solid (wavy) lines represent quarks or antiquarks (gluon). The left diagram has
${q_{1}+\bar{q}_2 \to q_{3}+\bar{q}_4}$ for${A(q_1\bar{q}_1)+B(q_2\bar{q}_2) \to} $ ${ C(q_3\bar{q}_1)+D(q_2\bar{q}_4)}$ , and the right diagram has${\bar{q}_1 + q_2 \to q_3 + \bar{q}_4}$ for$A(q_1\bar{q}_1)+B(q_2\bar{q}_2) \to C(q_1\bar{q}_4)+D(q_3\bar{q}_2)$ .Let
$E_A$ ($E_B$ ,$E_C$ ,$E_D$ ) and$J_{Az}$ ($J_{Bz}$ ,$J_{Cz}$ ,$J_{Dz}$ ) denote the energy and the magnetic projection quantum number of the angular momentum$J_A$ ($J_B$ ,$J_C$ ,$J_D$ ) of meson$A$ ($B, C, D$ ), respectively. From the four-momenta of mesons$A$ and$B$ ,$P_A$ and$P_B$ , the Mandelstam variable$s=(P_A+P_B)^2$ is defined. The unpolarized cross section for$A+B \to C+D$ depends on$\sqrt s$ and temperature$T$ . Let$\theta$ be the angle between$\vec{P}$ and$\vec{P}'$ which are the three-dimensional momenta of mesons$A$ and$C$ in the center-of-mass frame, respectively. The unpolarized cross section is [16]$ \begin{split} &\sigma^{\rm unpol}\left(\sqrt {s}, T\right) = \displaystyle\frac {1}{(2J_A+1)(2J_B+1)} \frac{1}{32\pi s}\displaystyle\frac{|\vec{P}^{\prime }(\sqrt{s})|}{|\vec{P}(\sqrt{s})|} \\ &\quad \times \int_{0}^{\pi }{\rm d}\theta \displaystyle\sum\limits_{J_{Az}J_{Bz}J_{Cz}J_{Dz}} \mid {\cal M}_{aq_1\bar{q}_2}+{\cal M}_{a\bar{q}_1q_2} \mid^2 \sin \theta, \end{split} $

(1) where
${\cal M}_{ aq_1\bar{q}_2}$ and${\cal M}_{ a\bar{q}_1q_2}$ are the transition amplitudes corresponding to the left diagram and the right diagram in Fig. 1, respectively. The transition amplitudes are given by$ \begin{split} &{\cal M}_{aq_1\bar {q}_2} = \displaystyle\frac {(m_{q_3}+m_{\bar{q}_1})^3}{m_{\bar{q}_1}^3} \sqrt {2E_A2E_B2E_C2E_D} \int {\rm d}\vec{r}_{q_1\bar{q}_1} {\rm d}\vec{r}_{q_2\bar{q}_4} \\ &\quad {\rm d}\vec{r}_{q_3\bar{q}_1, q_2\bar{q}_4}\psi_{q_3\bar {q}_1}^+ (\vec {r}_{q_3\bar {q}_1}) \psi_{q_2\bar {q}_4}^+ (\vec {r}_{q_2\bar {q}_4}) V_{{\rm a}q_1\bar{q}_2} \psi_{q_1\bar {q}_1} (\vec {r}_{q_1\bar {q}_1}) \\ &\quad\times \psi_{q_2\bar {q}_2} (\vec {r}_{q_2\bar {q}_2}){\rm e}^{{\rm i}\vec {p}_{q_1\bar {q}_1, q_2\bar {q}_2} \cdot \vec {r}_{q_1\bar {q}_1, q_2\bar {q}_2} -{\rm i}\vec {p}_{q_3\bar {q}_1, q_2\bar {q}_4} \cdot \vec {r}_{q_3\bar {q}_1, q_2\bar {q}_4}}, \end{split} $

(2) $ \begin{split} &{\cal M}_{a\bar{q}_1q_2} = \displaystyle\frac {(m_{q_1}+m_{\bar{q}_4})^3}{m_{q_1}^3} \sqrt {2E_A2E_B2E_C2E_D} \int {\rm d}\vec{r}_{q_1\bar{q}_1} {\rm d}\vec{r}_{q_3\bar{q}_2} \\ &\quad {\rm d}\vec{r}_{q_1\bar{q}_4, q_3\bar{q}_2} \psi_{q_1\bar {q}_4}^+ (\vec {r}_{q_1\bar {q}_4}) \psi_{q_3\bar {q}_2}^+ (\vec {r}_{q_3\bar {q}_2}) V_{{\rm a}\bar{q}_1q_2} \psi_{q_1\bar {q}_1} (\vec {r}_{q_1\bar {q}_1}) \\ &\quad\times \psi_{q_2\bar {q}_2} (\vec {r}_{q_2\bar {q}_2}) {\rm e}^{{\rm i}\vec {p}_{q_1\bar {q}_1, q_2\bar {q}_2} \cdot \vec {r}_{q_1\bar {q}_1, q_2\bar {q}_2} -{\rm i}\vec {p}_{q_1\bar {q}_4, q_3\bar {q}_2} \cdot \vec {r}_{q_1\bar {q}_4, q_3\bar {q}_2}}, \end{split} $

(3) where
$m_a$ is the mass of constituent$a$ ;$V_{ aq_1\bar{q}_2}$ and$V_{ a\bar{q}_1q_2}$ are the transition potentials for$q_1+\bar{q}_2 \to q_3+\bar{q}_4$ in the left diagram and$\bar{q}_1+q_2 \to q_3+\bar{q}_4$ in the right diagram of Fig. 1, respectively;$\psi_{ab}$ and$\vec{r}_{ab}$ are the wave function and the relative coordinate of constituents$a$ and$b$ , respectively. The relative coordinate and the relative momentum of$q_1\bar {q}_1$ and$q_2\bar {q}_2$ are denoted by$\vec {r}_{q_1\bar {q}_1, q_2\bar {q}_2}$ and$\vec {p}_{q_1\bar {q}_1, q_2\bar {q}_2}$ , respectively;$\vec {r}_{q_3\bar {q}_1, q_2\bar {q}_4}$ ,$\vec {p}_{q_3\bar {q}_1, q_2\bar {q}_4}$ ,$\vec {r}_{q_1\bar {q}_4, q_3\bar {q}_2}$ , and$\vec {p}_{q_1\bar {q}_4, q_3\bar {q}_2}$ are defined similarly. -
To calculate the transition amplitudes, we need the mesonic quark-antiquark wave functions and the transition potential for quark-antiquark annihilation and creation. The quark-antiquark annihilation and creation is shown in Fig. 2 with
$q (p_1) + \bar{q} (-p_2) \to q^{\prime} (p_3) + \bar{q}^{\prime} (-p_4)$ , where$p_1$ and$p_3$ ($p_2$ and$p_4$ ) are the four-momenta of quarks (antiquarks). The transition potential shown below is given in Ref. [16],$ \begin{split} V_{aq\bar{q}}(\vec {k}) = & \displaystyle\frac {g_{\rm s}^2}{k^2}\frac {\vec {\lambda}(34)}{2} \cdot \displaystyle\frac {\vec {\lambda}(21)}{2} \left( \displaystyle\frac {\vec {\sigma}(34) \cdot \vec{k} \vec {\sigma}(21) \cdot \vec{k}} {4m_{q^\prime} m_q} \right. \\ & {-\vec {\sigma}(34) \cdot \vec {\sigma}(21)} -\displaystyle\frac {\vec {\sigma}(21) \cdot \vec{p}_2 \vec {\sigma}(34) \cdot \vec {\sigma}(21) \vec {\sigma}(21) \cdot \vec{p}_1}{4m_q^2}\\ & \left. -\displaystyle\frac {\vec {\sigma}(34) \cdot \vec{p}_3 \vec {\sigma}(34) \cdot \vec {\sigma}(21) \vec {\sigma}(34) \cdot \vec{p}_4} {4m_{q^\prime}^2} \right), \end{split} $

(4) where
$ \vec{k} $ is the three-dimensional momentum of the gluon,$g_s$ is the gauge coupling constant,$m_{q}$ ($m_{q'}$ ) is the mass of the initial (final) quark,$\vec \lambda$ are the Gell-Mann matrices, and$\vec \sigma$ are the Pauli matrices.$\vec{\lambda}(21)$ ($\vec{\sigma}(21)$ ) denote matrix elements between the color (spin) wave functions of the initial quark and the initial antiquark, and$\vec{\lambda}(34)$ ($\vec {\sigma}(34)$ ) denote matrix elements between the color (spin) wave functions of the final quark and the final antiquark.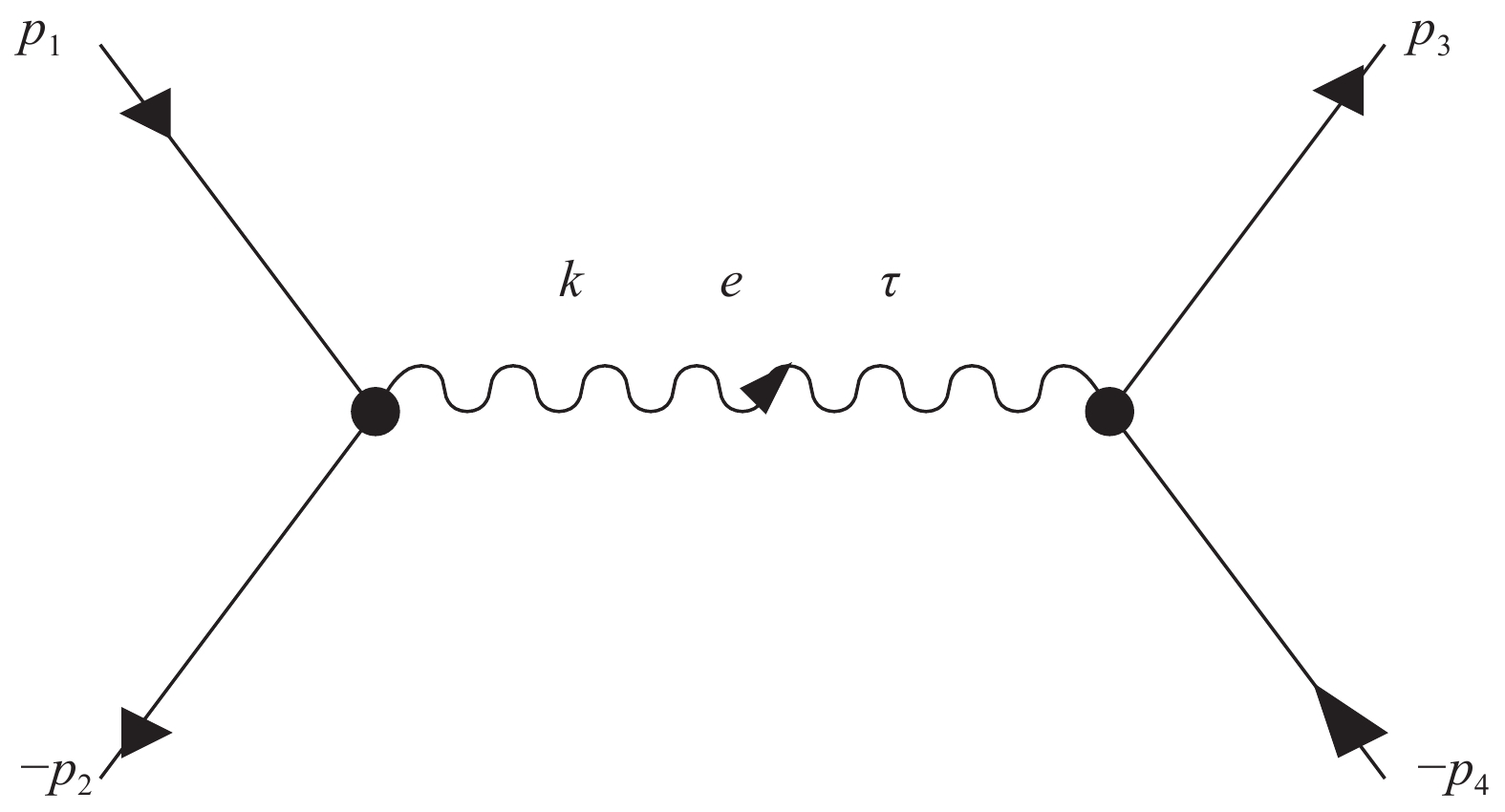
Figure 2. Corresponding to the process
${q(p_1)+\bar{q}(-p_2) \to } $ ${q'(p_3) +\bar{q}'(-p_4)}$ , solid (wavy) lines represent quarks or antiquarks (gluon). k denotes the gluon four-momentum, e its color index, and${\tau}$ its space-time index.The wave functions of mesons
$A$ ,$B$ ,$C$ , and$D$ are individually given by$ \psi_A =\phi_{A\rm rel} \phi_{A\rm color} \phi_{A\rm flavor} \chi_{S_A S_{Az}}, $

(5) $ \psi_B =\phi_{B\rm rel} \phi_{B\rm color} \phi_{B\rm flavor} \chi_{S_B S_{Bz}}, $

(6) $ \psi_C =\phi_{C\rm rel} \phi_{C\rm color} \phi_{C\rm flavor} \chi_{S_C S_{Cz}}, $

(7) $ \psi_D =\phi_{D\rm rel} \phi_{D\rm color} \phi_{D\rm flavor} \chi_{S_D S_{Dz}}, $

(8) where
$S_{i}$ is the spin of meson$i$ , and$S_{iz}$ is its magnetic projection quantum number. According to the two diagrams in Fig. 1,$\psi_A = \psi_{q_1\bar{q}_1}$ ,$\psi_B = \psi_{q_2\bar{q}_2}$ ,$\psi_C = \psi_{q_3\bar{q}_1} = \psi_{q_1\bar{q}_4}$ , and$\psi_D = \psi_{q_2\bar{q}_4} = \psi_{q_3\bar{q}_2}$ . The wave function of meson$i$ is made up of the quark-antiquark relative motion wave function$\phi_{i\rm rel}$ , the color wave function$\phi_{i\rm color}$ , the flavor wave function$\phi_{i\rm flavor}$ , and the spin wave function$\chi_{S_i S_{iz}}$ .The transition amplitudes contain color, spin, and flavor matrix elements. The color matrix elements related to the Gell-Mann matrices are 4/9 for the two diagrams in Fig. 1. The spin matrix elements related to the Pauli matrices are provided in Ref. [16]. Let
${\cal M}_{aq_1\bar{q}_2 f}$ and${\cal M}_{ a\bar{q}_1q_2f}$ represent the flavor matrix elements that correspond to the left and right diagrams in Fig. 1, respectively. The values of the flavor matrix elements are listed in Table 1,where$I$ is the total isospin of the two initial or final mesons for the reactions:$ \begin{array}{l} K \bar {K} \to K \bar {K}^\ast, K \bar{K} \to K^* \bar{K}, \pi K \to \pi K^\ast, \pi K \to \rho K,\\ \pi \pi \to K \bar{K}^\ast, \pi \pi \to K^\ast \bar{K}, \pi \pi \to K^\ast \bar{K}^\ast, \pi \rho \to K \bar{K}, \\ \pi \rho \to K^\ast \bar{K}^\ast, \rho \rho \to K^\ast \bar{K}^\ast, K \bar{K}^\ast \to \rho \rho, K^* \bar{K} \to \rho \rho. \end{array} $

The quark-antiquark relative-motion wave functions are given by the Schrödinger equation with a temperature-dependent potential. The experimental masses of ground-state mesons [20] are reproduced by the Schrödinger equation, while the up and down quark masses are 0.32 GeV, and the strange quark mass is 0.5 GeV [21]. The temperature-dependent potential between constituents
$a$ and$b$ is given by [21]$ V_{ab}(\vec {r}) = V_{\rm si}(\vec {r}) + V_{\rm ss}(\vec {r}), $

(9) where
$\vec{r}$ is the relative coordinate of$a$ and$b$ . The first term$V_{\rm si}(\vec{r})$ is the central spin-independent potential, and it depends on temperature:$\begin{split} V_{\rm {si}}(\vec {r}) =& - \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {3}{4} D \left[1.3-\left(\frac {T}{T_{\rm c}} \right)^4 \right] \tanh (Ar) \\ &+ \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {6\pi}{25} \frac {v(\lambda r)}{r} \exp (-Er), \end{split}$

(10) where
$D=0. 7$ GeV,$T_{\rm c}=0.175$ GeV,$A=1.5[0.75+0.25 $ $ (T/{T_{\rm c}})^{10}]^6$ GeV,$E=0. 6$ GeV,$\lambda=\sqrt{25/16\pi^2 \alpha'}$ with$\alpha'=1.04$ GeV−2,$\vec{\lambda}_a$ ($\vec{\lambda}_b$ ) are the Gell-Mann matrices for the color generators of the constituent a (b), and the dimensionless function$v(x)$ is given by Buchmüller and Tye in Ref. [22].This potential
$V_{\rm si}(\vec{r})$ is relevant to the temperature of hadronic matter and the distance$r$ . It shows some characteristics as follows. At very short distances$r < 0.01$ fm, the potential arises from one-gluon exchange and perturbative one- and two-loop corrections. At large distances and blow the QCD phase-transition temperature$T_{\rm c}$ , the color screening produced by high-temperature medium may be strong. Karsch et al. [23] have provided such a numerical quark-antiquark potential at$r \geqslant 0.3$ fm in a temperature region from lattice QCD calculations. When the distance between the quark and the antiquark becomes large, the quark-antiquark potential at a given temperature becomes a constant value, which decreases with an increase in the temperature.The second term
$V_{\rm ss}(\vec{r})$ in Eq. (9) is the spin-spin interaction, which originates from one-gluon exchange and perturbative one- and two-loop corrections [24]; it depends on the constituent masses, and includes relativistic effects [1-4, 25]:$\begin{split} V_{\rm ss}(\vec {r})=& -\frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {16\pi^2}{25}\frac{d^3}{\pi^{3/2}}\exp(-d^2r^2) \frac {\vec {s}_a \cdot \vec {s} _b} {m_am_b}\\ & + \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2}\frac {4\pi}{25} \frac {1} {r} \frac {d^2v(\lambda r)}{dr^2} \frac {\vec {s}_a \cdot \vec {s}_b}{m_am_b}, \end{split}$

(11) where
$\vec{s}_a$ ($\vec{s}_b$ ) is the spin of constituent$a$ ($b$ ), and$d$ is given by$ d^2=d_1^2\left[\frac{1}{2}+\frac{1}{2}\left(\frac{4m_a m_b}{(m_a+m_b)^2} \right)^4\right]+d_2^2\left(\frac{2m_am_b}{m_a+m_b}\right)^2, $

(12) where
$d_1=0.15$ GeV and$d_2= 0.705$ . -
We consider the following inelastic meson-meson scattering processes that mainly take the two Feynman diagrams in Fig. 1:
$ \begin{array}{l} K \bar {K} \to K \bar {K}^\ast, \quad K \bar{K} \to K^* \bar{K}, \quad \pi K \to \pi K^\ast, \quad \pi K \to \rho K,\\ \pi \pi \to K \bar{K}^\ast, \quad \pi \pi \to K^\ast \bar{K}, \quad \pi \pi \to K^\ast \bar{K}^\ast, \quad \pi \rho \to K \bar{K},\\ \pi \rho \to K^\ast \bar{K}^\ast, \quad \rho \rho \to K^\ast \bar{K}^\ast, \quad K \bar{K}^\ast \to \rho \rho, \quad K^* \bar{K} \to \rho \rho. \end{array} $

The total spin of
$\pi$ and$K$ mesons is not equal to the total spin of$\pi$ and$K^*$ mesons or of$\rho$ and$K$ mesons, i.e., the total spin in either$\pi K \to \pi K^*$ or$\pi K \to \rho K$ is not conserved. Thus, quark interchange does not occur in the two reactions.${\cal M}_{aq_1\bar {q}_2}$ and${\cal M}_{a\bar{q}_1q_2}$ are proportional to the flavor matrix elements. If the transition amplitudes equal zero, the unpolarized cross section given in Eq. (1) is zero. As seen in Table 1, the flavor matrix elements for the two reactions for$I=3/2$ are zero. Quark-antiquark annihilation and creation does not happen in the two reactions for$I=3/2$ , too. Therefore, cross sections for$\pi K \to \pi K^*$ for$I=3/2$ and$\pi K \to \rho K$ for$I=3/2$ are zero in the present work; however, we still investigate$\pi K \to \pi K^*$ for$I=1/2$ and$\pi K \to \rho K$ for$I=1/2$ of which${\cal M}_{ a\bar{q}_1q_2f}$ are not zero. The other reactions must involve quark-antiquark annihilation and creation, but do not involve quark interchange.It is shown in Table 1 that only the right diagram in Fig. 1 contributes to the reactions
$\pi \pi \to K \bar{K}^*$ ,$\pi \pi \to K^\ast \bar{K}$ ,$\pi \pi \to K^\ast \bar{K}^*$ ,$\pi \rho \to K \bar{K}$ ,$\pi \rho \to K^* \bar{K}^\ast$ ,$\rho \rho \to K^* \bar{K}^*$ ,$K \bar{K}^* \to \rho \rho$ , and$K^\ast \bar{K} \to \rho \rho$ . Because the flavor matrix elements for the reactions for$I=0$ are$\sqrt {6}/2$ times the ones for$I=1$ , the cross sections for the reactions for$I=0$ are 1.5 times the cross sections for$I=1$ . The cross section for$K\bar{K} \to K^*\bar{K}$ ($\pi \pi \to K^* \bar{K}$ ,$K^*\bar{K} \to \rho\rho$ ) equals the one for$K\bar{K} \to K\bar{K}^*$ ($\pi \pi \to K\bar{K}^*$ ,$K\bar{K}^* \to \rho \rho$ ). Thus, we do not plot the cross sections for$K\bar{K} \to K^*\bar{K}$ ,$\pi \pi \to K^* \bar{K}$ , and$K^*\bar{K} \to \rho \rho$ .The gauge coupling constant is
$\displaystyle \frac{2\sqrt{6}\pi}{5}$ for quark-antiquark annihilation and creation [19, 22]. According to Eq. (1), we calculate unpolarized cross sections at the six temperatures$T/T_{\rm c} =0$ , 0.65, 0.75, 0.85, 0.9, and 0.95. In Figs. 3-12 we plot the unpolarized cross sections for the following ten channels:$ \begin{array}{l} I=1\; K \bar {K} \to K \bar {K}^\ast, \;\; I=0\; K \bar{K} \to K \bar{K}^\ast, \;\; I=1/2\; \pi K \to \pi K^\ast, \\ I=1/2\; \pi K \to \rho K, \quad I=1\; \pi \pi \to K \bar{K}^\ast, \quad I=1\; \pi \pi \to K^\ast \bar{K}^\ast, \\ I=1\; \pi \rho \to K \bar{K}, \quad I=1\; \pi \rho \to K^\ast \bar{K}^\ast, \\ I=1\; \rho \rho \to K^\ast \bar{K}^\ast, \quad I=1\; K \bar{K}^\ast \to \rho\rho. \end{array} $

The last channel is endothermic at
$T/T_{\rm c}=0$ and exothermic at$T/T_{\rm c}=0.65$ , 0.75, 0.85, 0.9, and 0.95. The other nine channels are endothermic. The numerical cross sections for endothermic reactions are parametrized as$ \begin{split} \!\!\!\!\sigma^{\rm unpol}(\sqrt {s}, T) =& a_1 \left(\displaystyle \frac {\sqrt {s}\! -\!\sqrt {s_0}} {b_1} \right)^{e_1} \exp \left[e_1 \left(1\!-\!\displaystyle \frac {\sqrt {s}\!-\!\sqrt {s_0}} {b_1} \right) \right] \\ & + a_2 \left(\displaystyle \frac {\sqrt {s} -\sqrt {s_0}} {b_2} \right)^{e_2} \exp \left[e_2 \left(1-\displaystyle \frac {\sqrt {s}-\sqrt {s_0}} {b_2} \right) \right], \end{split} $

(13) where
$\sqrt{s_0}$ is the threshold energy, and$a_1$ ,$b_1$ ,$e_1$ ,$a_2$ ,$b_2$ , and$e_2$ are parameters. The numerical cross sections for exothermic reactions are parametrized as
Figure 5. (color online) Cross sections for
${\pi K \to \pi K^\ast}$ for I= 1/2 at various temperatures.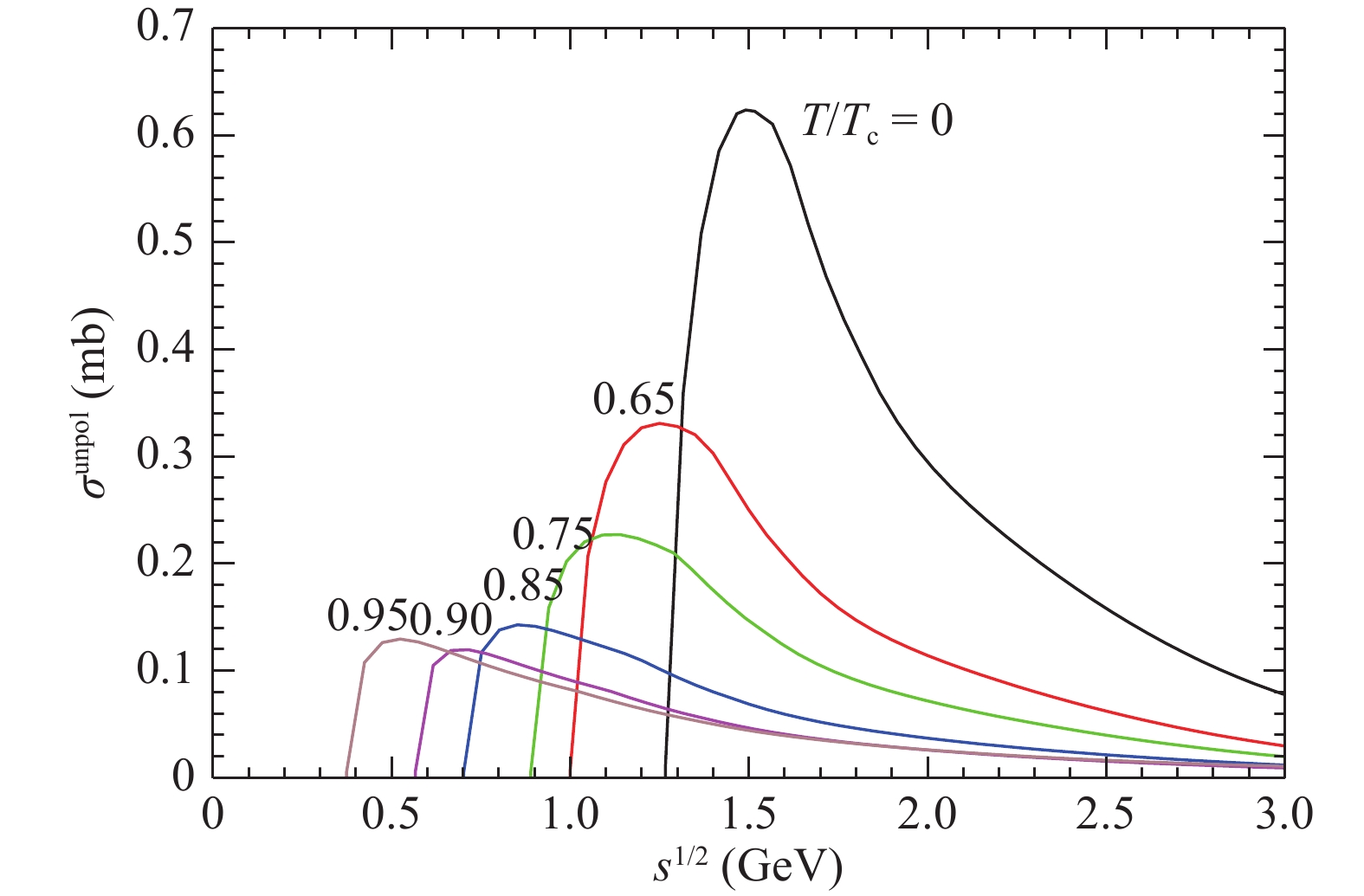
Figure 6. (color online) Cross sections for
${\pi K \to \rho K}$ for I= 1/2 at various temperatures.
Figure 7. (color online) Cross sections for
${\pi \pi \to K \bar{K}^\ast}$ for I= 1 at various temperatures.$ \begin{split} &\sigma^{\rm unpol}(\sqrt {s}, T) =\displaystyle \frac{\vec{P}^{\prime 2}}{\vec{P}^2} \left\{a_1 \left(\displaystyle \frac {\sqrt {s} \!-\!\sqrt {s_0}} {b_1} \right)^{e_1} \exp \left[e_1 \left(1\!-\!\displaystyle \frac {\sqrt {s}\!-\!\sqrt {s_0}} {b_1} \right) \right] \right. \\ &\quad + \left. a_2 \left(\displaystyle \frac {\sqrt {s} -\sqrt {s_0}} {b_2} \right)^{e_2} \exp \left[e_2 \left(1-\displaystyle \frac {\sqrt {s}-\sqrt {s_0}} {b_2} \right) \right] \right\}.\quad\quad\quad\;\;(14) \end{split} $

The parameter values are listed in Tables 2-4. In the three tables the quantity
$d_0$ is the separation between the peak's location on the$\sqrt s$ -axis and the threshold energy. The smaller$d_0$ is, the faster the cross section increases from zero to the peak cross section. The quantity$\sqrt{s_z}$ is the square root of the Mandelstam variable at which the cross section is 1/100 of the peak cross section. The quantity$\sqrt{s_z}-\sqrt{s_0}-d_0$ is the difference between$\sqrt{s_z}$ and the peak's location on the$\sqrt{s}$ -axis. The smaller$\sqrt{s_z}-\sqrt{s_0}-d_0$ is, the faster the cross section decreases from the peak cross section to zero.The potential given in Eq. (9) depends on the temperature. The Schrödinger equation with the potential yields temperature-dependent meson masses. For any endothermic (exothermic) 2-to-2 meson-meson reaction the threshold energy is the sum of the masses of the two final (initial) mesons. Because the meson masses decrease with increasing temperature, the threshold energy decreases with increasing temperature.
reactions ${T/T_{\rm c} }$ 

${a_1}$ 

${b_1}$ 

${e_1}$ 

${a_2}$ 

${b_2}$ 

${e_2}$ 

${d_0}$ 

${\sqrt{s_{ z}} }$ 

${I=1 \; \pi\pi\to K \bar{K}^{*} }$ 

0 0.15 0.25 0.7 0.03 0.28 2.2 0.3 3.69 0.65 0.06 0.2 1.0 0.09 0.24 0.5 0.2 3.3 0.75 0.016 0.35 0.4 0.095 0.19 0.6 0.2 3.17 0.85 0.004 0.41 0.2 0.06 0.2 0.6 0.2 3.0 0.9 0.011 0.26 0.3 0.041 0.2 0.7 0.2 2.91 0.95 0.01 0.17 0.3 0.06 0.22 0.6 0.25 2.82 ${I=1 \; \pi\pi\to K^{*} \bar{K}^{*} }$ 

0 0.09 0.22 1.0 0.3 0.31 0.7 0.25 4.76 0.65 0.13 0.5 1.9 0.098 0.09 0.6 0.3 3.61 0.75 0.024 0.83 8.0 0.09 0.225 0.56 0.3 3.35 0.85 0.013 0.98 8.6 0.022 0.24 0.54 0.35 3.08 0.9 0.008 1.13 7.42 0.012 0.26 0.5 0.45 3.03 0.95 0.003 1.42 15.0 0.0181 0.41 0.5 0.35 3.01 ${I=1 \; \pi\rho\to K \bar{K} }$ 

0 0.55 0.3 2.6 0.58 0.174 0.6 0.3 2.98 0.65 0.082 0.25 1.7 0.19 0.163 0.5 0.2 3.04 0.75 0.027 0.22 1.5 0.11 0.17 0.5 0.2 3.09 0.85 0.003 0.23 2.4 0.053 0.18 0.5 0.2 3.11 0.9 0.005 0.5 1.3 0.04 0.16 0.5 0.2 3.08 0.95 0.01 0.46 1.2 0.04 0.16 0.5 0.2 2.97 Table 3. The same as Table 2, but for three other reactions.
Let
$m_A$ ($m_B$ ,$m_C$ ,$m_D$ ) be the mass of meson$A$ ($B$ ,$C$ ,$D$ ). In terms of the meson masses we have$ \begin{array}{l} \mid \vec{P} \mid =\displaystyle\frac {1}{2} \sqrt {\displaystyle\frac {(s-m_A^2-m_B^2)^2-4m_A^2m_B^2}{s}}, \\ \mid \vec{P}^\prime \mid =\displaystyle\frac {1}{2} \sqrt {\displaystyle\frac {(s-m_C^2-m_D^2)^2-4m_C^2m_D^2}{s}}. \end{array} $

For endothermic reactions the threshold energy is
$\sqrt{s_0}=m_C+m_D$ , and we obtain$ \frac {\mid \vec{P}^\prime \mid}{\mid \vec{P} \mid} = \sqrt {\frac {(\sqrt{s}-\sqrt{s_0})(\sqrt{s}+\sqrt{s_0})[s-(m_C-m_D)^2]} {[s-(m_A+m_B)^2][s-(m_A-m_B)^2]}}. $

When
$\sqrt s$ is close to$\sqrt {s_0}$ ,$\displaystyle\frac {\mid \vec{P}^\prime \mid} {\mid \vec{P} \mid}$ is sensitive to$\sqrt {s} - \sqrt {s_0}$ . Because Eq. (1) contains$\displaystyle\frac {\mid \vec{P}^\prime \mid}{\mid \vec{P} \mid}$ , the unpolarized cross section in Eq. (13) may be proportional to$(\sqrt {s} - \sqrt {s_0})^{0.5}$ . Nevertheless, the factor$\sqrt {\displaystyle\frac {(\sqrt{s}+\sqrt{s_0})[s-(m_C-m_D)^2]} {[s-(m_A+m_B)^2][s-(m_A-m_B)^2]}}$ in the expression of$\displaystyle\frac {\mid \vec{P}^\prime \mid} {\mid \vec{P} \mid}$ and the factor$\displaystyle\frac {1}{s} \mid {\cal M}_{aq_1\bar{q}_2}+{\cal M}_{ a\bar{q}_1q_2} \mid^2$ in Eq. (1) modify the dependence of the unpolarized cross section on$\sqrt {s} - \sqrt {s_0}$ . Therefore, we use$(\sqrt {s} - \sqrt {s_0})^{e_1}$ and$(\sqrt {s} - \sqrt {s_0})^{e_2}$ in Eq. (13) instead of$(\sqrt {s} - \sqrt {s_0})^{0.5}$ . Indeed, it can be observed from Tables 2-4 that the values of$e_1$ and/or$e_2$ are near 0.5.$\sigma_{\rm num}^{\rm unpol}(\sqrt{s}, T)$ denotes the cross sections calculated from Eq. (1), which are plotted in Figs. 3-12. By comparison,$\sigma_{\rm para}^{\rm unpol}(\sqrt{s}, T)$ denotes the cross sections given by Eqs. (13) and (14). We change$a_1$ ,$b_1$ ,$e_1$ ,$a_2$ ,$b_2$ , and$e_2$ to make$\mid (\sigma_{\rm para}^{\rm unpol}(\sqrt{s}, T) -\sigma_{\rm num}^{\rm unpol}(\sqrt{s}, T))/ \sigma_{\rm num}^{\rm unpol}(\sqrt{s}, T) \mid$ as small as possible. The parameter values that make$\mid (\sigma_{\rm para}^{\rm unpol}(\sqrt{s}, T) -\sigma_{\rm num}^{\rm unpol}(\sqrt{s}, T))/ \sigma_{\rm num}^{\rm unpol}(\sqrt{s}, T) \mid$ smallest are provided in Tables 2-4.reactions ${T/T_{\rm c} }$ 

${a_1}$ 

${b_1}$ 

${e_1}$ 

${a_2}$ 

${b_2}$ 

${e_2}$ 

${d_0}$ 

${\sqrt{s_{ z}} }$ 

${I=1 \; \pi\rho\to K^{*}\bar{K}^{*}}$ 

0 0.4 0.61 2.0 0.6 0.13 0.7 0.225 4.77 0.65 0.048 0.78 3.9 0.073 0.17 0.6 0.35 3.96 0.75 0.017 0.13 0.6 0.024 0.7 3.1 0.55 3.65 0.85 0.0012 0.1 0.63 0.006 0.65 1.88 0.75 3.18 0.9 0.0019 0.13 0.63 0.0051 0.66 1.81 0.5 3.02 0.95 0.01 0.544 1.1 0.006 0.1 0.5 0.25 2.9 ${I=1 \; \rho\rho\to K^{*}\bar{K}^{*}}$ 

0 3 0.1 0.72 1.49 0.32 0.5 0.1 4.23 0.65 0.165 0.16 0.54 0.1 0.98 4.5 0.15 3.98 0.75 0.016 1.0 4.0 0.04 0.26 0.6 0.25 3.72 0.85 0.0104 0.377 1.21 0.0017 0.58 0.57 0.3 3.25 0.9 0.006 0.29 2.1 0.01 0.36 0.78 0.25 2.9 0.95 0.017 0.32 0.5 0.031 0.21 1.3 0.2 2.53 ${I=1 \; K\bar{K}^{*}\to \rho\rho}$ 

0 2.2 0.11 0.7 1.0 0.29 0.3 0.1 4.6 0.65 0.18 0.33 0.23 0.35 0.05 0.6 0.05 4.0 0.75 0.048 0.87 1.7 0.09 0.07 0.45 0.05 3.96 0.85 0.006 1.18 4.2 0.012 0.19 0.51 0.2 3.56 0.9 0.005 0.092 0.6 0.007 0.7 1.7 0.3 3.4 0.95 0.002 1.21 18 0.01 0.32 0.5 0.25 3.28 Table 4. The same as Table 2, but for three other reactions.
A feature of the endothermic reactions in Figs. 3-11 is that the peak cross section decreases first and then increases as the temperature increases. As the temperature increases from zero, confinement shown by the potential in Eq. (10) gradually becomes weaker, the Schrödinger equation produces increasing meson radii, and the mesonic quark-antiquark states become looser and looser. On one hand, as the temperature increase, the weakening confinement makes combining final quarks and antiquarks to form final mesons more difficult, and thus reduces the cross sections. On the other hand, the increase in the radii of initial mesons causes an increase in the cross sections as the temperature increases. The two factors determine the change in peak cross section with respect to the temperature. Another feature is that the cross section increases rapidly from zero to a maximum value when the total energy of the two initial mesons in the center-of-mass frame increases from the threshold energy; the cross section further decreases from the maximum value or exhibits a plateau on the right of the peak as seen in Figs. 8 and 10.

Figure 10. (color online) Cross sections for
${\pi \rho \to K^\ast \bar{K}^\ast}$ for I= 1 at various temperatures.
Figure 11. (color online) Cross sections for
${\rho \rho \to K^\ast \bar{K}^\ast}$ for I= 1 at various temperatures.The unpolarized cross sections for
$K \bar{K} \to K \bar{K}^\ast$ for$I=1$ and for$I=0$ are shown in Figs. 3 and 4, respectively. Quark-antiquark annihilation and creation takes place in the two isospin channels. If${\cal M}_{aq_1\bar {q}_2}$ (${\cal M}_{ a\bar{q}_1q_2}$ ) for a reaction equals zero, the left (right) diagram does not contribute to the reaction. From Table 1,it can be observed that the two diagrams in Fig. 1 contribute to$K \bar{K} \to K \bar{K}^\ast$ for$I=0$ , and only the right diagram contributes to$K \bar{K} \to K \bar{K}^\ast$ for$I=1$ . The peak cross section of$K \bar{K} \to K \bar{K}^\ast$ for$I=0$ at a given temperature is more than four times the one for$I=1$ , and$\sqrt{s_z}$ for$I=0$ in Table 2 is approximately two times that for$I=1$ . When$T/T_{\rm c} =0$ , 0.65, and 0.75,$d_0$ of$K \bar{K} \to K \bar{K}^\ast$ for$I=0$ is equal to$d_0$ for$I=1$ ; when$T/T_{\rm c}=0.85$ , 0.90, and 0.95,$d_0$ of$K \bar{K} \to K \bar{K}^\ast$ for$I=0$ is less than$d_0$ for$I=1$ . Therefore, the cross section for$K\bar{K} \to K\bar{K}^*$ for$I=0$ is larger than the one for$K\bar{K} \to K\bar{K}^*$ for$I=1$ .reactions ${T/T_{\rm c} }$ 

${a_1}$ 

${b_1}$ 

${e_1}$ 

${a_2}$ 

${b_2}$ 

${e_2}$ 

${d_0}$ 

${\sqrt{s_{z}} }$ 

${I=1 \; K\bar{K}\to K \bar{K}^{*}}$ 

0 0.14 0.173 0.3 1.27 0.124 0.6 0.125 3.06 0.65 0.1 0.209 0.2 0.9 0.142 0.7 0.15 2.91 0.75 0.1 0.26 1.0 0.69 0.128 0.5 0.15 2.87 0.85 0.1 0.03 0.5 0.4 0.157 0.51 0.1 2.82 0.9 0.2 0.04 0.6 0.35 0.153 0.41 0.075 2.77 0.95 0.3 0.21 0.5 0.32 0.035 0.45 0.05 2.76 ${I=0 \; K\bar{K}\to K \bar{K}^{*}}$ 

0 4.0 0.108 0.63 3.05 0.251 0.44 0.125 7.21 0.65 3.3 0.127 0.67 1.5 0.267 0.35 0.15 6.12 0.75 2.5 0.114 0.56 1.3 0.25 0.39 0.15 5.78 0.85 1.1 0.059 0.5 1.4 0.195 0.45 0.075 5.58 0.9 1.4 0.183 0.4 1.7 0.04 0.5 0.05 5.34 0.95 1.6 0.16 0.33 2.0 0.03 0.52 0.025 5.74 ${ I=1/2 \; \pi K\to\pi K^{*} }$ 

0 0.4 0.22 1.5 0.45 0.329 0.5 0.225 6.47 0.65 0.3 0.18 1.0 0.26 0.275 0.4 0.25 5.78 0.75 0.1 0.33 0.3 0.33 0.2 0.8 0.25 5.71 0.85 0.2 0.17 0.5 0.04 0.439 0.4 0.15 5.81 0.9 0.07 0.1 0.9 0.17 0.219 0.4 0.15 6.05 0.95 0.1 0.1 0.5 0.15 0.308 0.47 0.15 6.23 ${ I=1/2 \; \pi K\to \rho K }$ 

0 0.309 0.33 0.5 0.33 0.18 1.1 0.225 6.22 0.65 0.061 0.84 0.29 0.29 0.21 0.8 0.25 4.81 0.75 0.15 0.19 0.8 0.09 0.34 0.4 0.25 4.78 0.85 0.055 0.4 0.5 0.1 0.14 0.5 0.15 4.94 0.9 0.05 0.61 1.4 0.11 0.1 0.5 0.15 5.02 0.95 0.05 0.71 1.6 0.12 0.12 0.5 0.15 5.37 Table 2. Values of the parameters. a1 and a2 are in units of millibarns; b1, b2, d0, and
${\sqrt{s_{\rm z}}}$ are in units of GeV; e1 and e2 are dimensionless.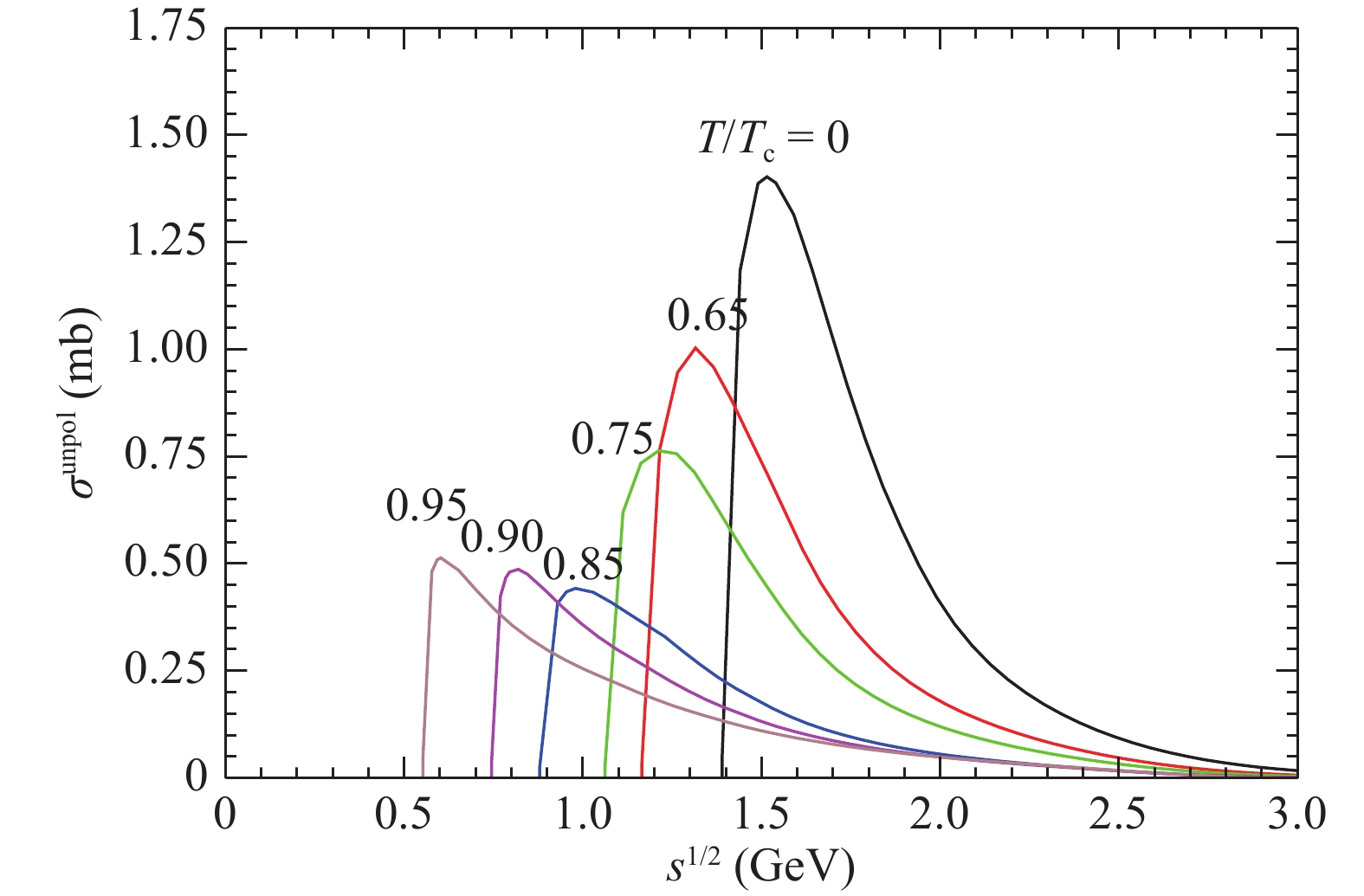
Figure 3. (color online) Cross sections for
${K \bar{K} \to K \bar{K}^\ast}$ for I= 1 at various temperatures.
Figure 4. (color online) Cross sections for
${K \bar{K} \to K \bar{K}^\ast}$ for I= 0 at various temperatures.The unpolarized cross section for
$K\bar{K}\to\rho\rho$ for$I=1$ is shown in Fig. 15 of Ref. [16], and that for$K\bar{K}^{\ast}\to \rho\rho$ for$I=1$ is shown in Fig. 12 in the present work. At zero temperature, the peak cross section for$K\bar{K}\to\rho\rho$ for$I=1$ is smaller than that for$K\bar{K}^*\to\rho\rho$ for$I=1$ ; the cross section for$K\bar{K}\to\rho\rho$ for$I=1$ decreases from the peak cross section slower than that for$K\bar{K}^*\to\rho\rho$ for$I=1$ because$\sqrt s_z$ of the former is larger than that of the latter. When the two reactions are exothermic, the cross section for$K\bar{K}\to\rho\rho$ for$I=1$ decreases slower than that for$K\bar{K}^*\to\rho\rho$ for$I=1$ with increasing center-of-mass energy of the two initial mesons from the threshold energy plus 10−4 GeV.
Figure 12. (color online) Cross sections for
${K \bar{K}^\ast \to \rho \rho}$ for I=1 at various temperatures.In the present work and in Ref. [16], we studied the following reactions:
$K\bar{K} \to K\bar{K}^*$ ,$K^*\bar{K}$ , and$K^*\bar{K}^*$ ;$\pi\pi \to K\bar{K}$ ,$K\bar{K}^*$ ,$K^*\bar{K}$ , and$K^*\bar{K}^*$ ;$\pi\rho \to K\bar{K}$ ,$K\bar{K}^*$ ,$K^*\bar{K}$ , and$K^*\bar{K}^*$ . As an example, we compare the production of$K\bar{K}^*$ with the production of$K^*\bar{K}^*$ in the$K+\bar K$ reaction. The unpolarized cross sections for$K\bar{K} \to K^{\ast} \bar{K}^\ast$ for$I=1$ and for$I=0$ are shown in Figs. 8 and 9 of Ref. [16], respectively. Quark-antiquark annihilation and creation takes place in the two isospin channels. The peak cross section for$K \bar{K} \to K \bar{K}^\ast$ for$I=1$ ($I=0$ ) at a given temperature is larger than that for$K \bar{K} \to K^* \bar{K}^\ast$ for$I=1$ ($I=0$ ). The Mandelstam variable$\sqrt s$ corresponding to the peak cross section for$K\bar{K} \to K\bar{K}^*$ is smaller than that corresponding to the peak cross section for$K\bar{K} \to K^*\bar{K}^*$ at a given temperature. Because the two reactions have the same initial mesons, the initial mesons in$K\bar{K} \to K\bar{K}^*$ have a smaller value of$\mid{\vec{P}}\mid$ , corresponding to the peak cross section than in$K \bar{K} \to K^{\ast} \bar{K}^\ast$ . The cross section given by Eq. (1) is proportional to the inverse of$s\mid{\vec{P}}\mid$ . Therefore, the peak cross section for$K \bar{K} \to K \bar{K}^\ast$ is larger than that for$K \bar{K} \to K^{\ast} \bar{K}^\ast$ .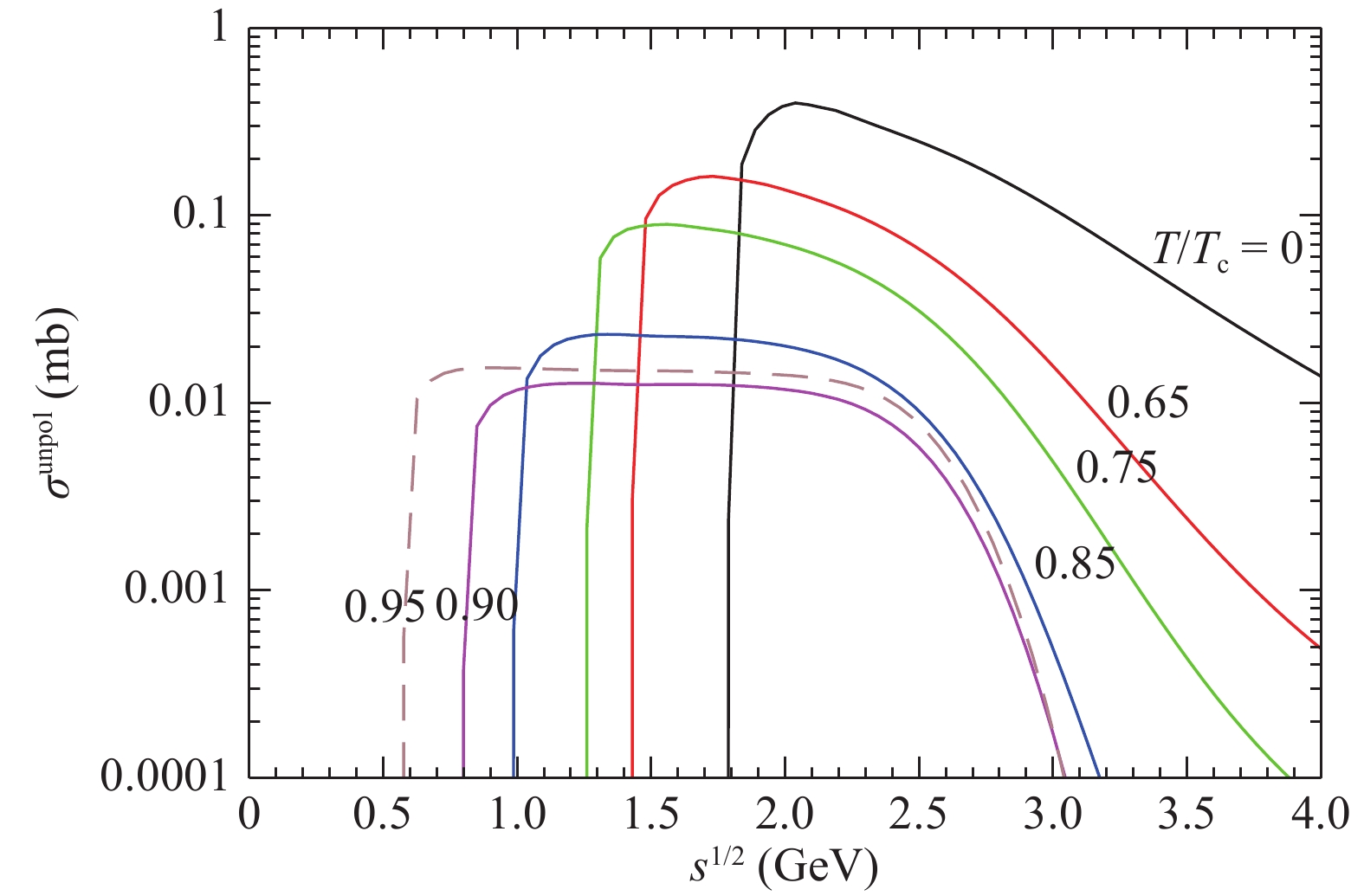
Figure 8. (color online) Cross sections for
${\pi \pi \to K^\ast \bar{K}^\ast}$ for I= 1 at various temperatures.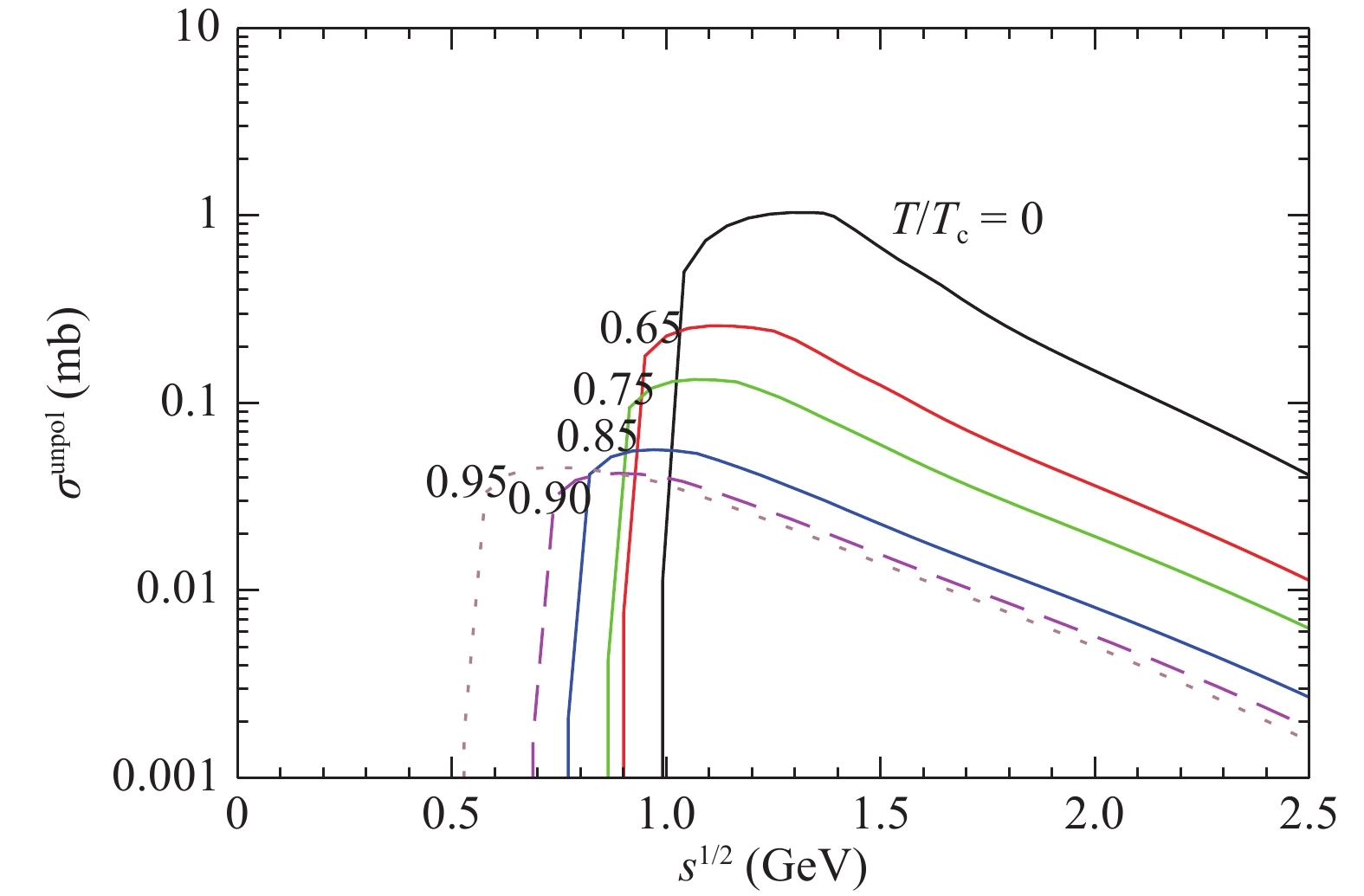
Figure 9. (color online) Cross sections for
${\pi \rho \to K \bar{K}}$ for I= 1 at various temperatures.The total spin of the two final mesons may not equal the total spin of the two initial mesons in the reactions in the present work. This can be attributed to a quark-antiquark potential, which is equivalent to the transition potential in Eq. (4). The quark-antiquark potential is obtained from the transition potential under the Fierz transformations in Ref. [16],
$ \begin{split} &V_{aq\bar{q}F}(\vec{k}) = -\displaystyle\frac{g^{2}_s}{k^2} \left[\displaystyle\frac{1}{3}\lambda^{0}_{f}(31)\lambda^{0}_{f}(42) +\displaystyle\frac{1}{2}\vec{\lambda}_{f}(31)\cdot\vec{\lambda}^{T}_{f}(42)\right] \times \left[\displaystyle\frac{4}{9}\lambda^{0}(31)\lambda^{0}(42) -\displaystyle\frac{1}{12}\vec{\lambda}(31)\cdot\vec{\lambda}^{T}(42)\right] \left[-\displaystyle\frac{3}{2}-\frac{1}{2}\vec{\sigma}(31)\cdot\vec{\sigma}(42) \right. \\ &\;+ \displaystyle\frac{\vec{\sigma}(42)\cdot\vec{p}_{4} \vec{\sigma}(42)\cdot\vec{p}_{2}} {8m_{q}m_{q'}} +\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{3} \vec{\sigma}(31)\cdot\vec{p}_{1}} {8m_{q}m_{q'}} +\displaystyle\frac{3\vec{\sigma}(31)\cdot\vec{p}_{1} \vec{\sigma}(42)\cdot\vec{p}_{2}} {8m^{2}_{q}} -\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{1} \vec{\sigma}(42)\cdot\vec{p}_{4}} {8m_{q}m_{q'}} -\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{3} \vec{\sigma}(42)\cdot\vec{p}_{2}} {8m_{q}m_{q'}} \\ &\; +\displaystyle\frac{3\vec{\sigma}(31)\cdot\vec{p}_{3} \vec{\sigma}(42)\cdot\vec{p}_{4}} {8m^{2}_{q'}}+ \displaystyle\frac{\vec{\sigma}(31)\vec{\sigma}(31)\cdot\vec{p}_{1} \vec{\sigma}(42)\vec{\sigma}(42)\cdot\vec{p}_{2}}{8m^{2}_{q}} +\displaystyle\frac{\vec{\sigma}(31)\vec{\sigma}(31)\cdot\vec{p}_{1} \vec{\sigma}(42)\cdot\vec{p}_{4}\vec{\sigma}(42)}{8m_{q}m_{q'}} + \displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{3}\vec{\sigma}(31)\cdot \vec{\sigma}(42)\vec{\sigma}(42)\cdot\vec{p}_{2}}{8m_{q}m_{q'}} \\ &\;+\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{3}\vec{\sigma}(31) \vec{\sigma}(42)\cdot\vec{p}_{4}\vec{\sigma}(42)}{8m^{2}_{q'}}-\left. \displaystyle\frac{\vec{\sigma}(42)\cdot\vec{p}_{4}\vec{\sigma}(31)\cdot \vec{\sigma}(42)\vec{\sigma}(42)\cdot\vec{p}_{2}}{8m_{q}m_{q'}} -\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{3}\vec{\sigma}(31)\cdot \vec{\sigma}(42)\vec{\sigma}(31)\cdot\vec{p}_{1}}{8m_{q}m_{q'}} \right], \quad\quad\quad\quad\quad\quad\;\;(15) \end{split} $

where
$\lambda^0_f$ is a$3\times3$ unit matrix in flavor space,$\vec{\lambda}_f$ are the Gell-Mann matrices that operate in flavor space, and$\lambda^0$ is a$3\times3$ unit matrix in color space. The superscript$T$ in Eqs. (15), (16), and (19)-(21) denotes transposition [26].For the left diagram in Fig. 1, the quark-antiquark potential corresponding to
$q_1+\bar q_2 \to q_3 + \bar q_4$ is between$q_1$ and$\bar{q}_2$ ,$ \begin{split} &V_{aq_1\bar{q}_2F}(\vec{k}) = -\displaystyle\frac{g^{2}_s}{k^2}\left[\frac{1}{3}\lambda^{0}_{f}(31)\lambda^{0}_{f}(42) +\displaystyle\frac{1}{2}\vec{\lambda}_{f}(31)\cdot\vec{\lambda}^{T}_{f}(42)\right] \times \left[\displaystyle\frac{4}{9}\lambda^{0}(31)\lambda^{0}(42)-\displaystyle\frac{1}{12} \vec{\lambda}(31)\cdot\vec{\lambda}^{T}(42)\right] \left[-\displaystyle\frac{3}{2}-\frac{1}{2} \vec{\sigma}(31)\cdot\vec{\sigma}(42) \right. \\ &\quad + \displaystyle\frac{\vec{\sigma}(42)\cdot\vec{p}_{{\bar q_4}}\vec{\sigma}(42)\cdot \vec{p}_{{{\bar q_2}}}}{8m_{q_1}m_{q_3}} +\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{q_3}\vec{\sigma}(31)\cdot \vec{p}_{q_1}}{8m_{q_1}m_{q_3}} +\displaystyle\frac{3\vec{\sigma}(31)\cdot\vec{p}_{q_1} \vec{\sigma}(42)\cdot \vec{p}_{\bar q_2}}{8m^{2}_{q_1}} -\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{q_1} \vec{\sigma}(42)\cdot \vec{p}_{\bar q_4}}{8m_{q_1}m_{q_3}} -\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{q_3} \vec{\sigma}(42)\cdot \vec{p}_{\bar q_2}}{8m_{q_1}m_{q_3}} \\ &\quad+\displaystyle\frac{3\vec{\sigma}(31)\cdot\vec{p}_{q_3} \vec{\sigma}(42)\cdot \vec{p}_{\bar q_4}}{8m^{2}_{q_3}}+ \displaystyle\frac{\vec{\sigma}(31)\vec{\sigma}(31)\cdot\vec{p}_{q_1} \vec{\sigma}(42)\vec{\sigma}(42)\cdot\vec{p}_{\bar q_2}}{8m^{2}_{q_1}} +\displaystyle\frac{\vec{\sigma}(31)\vec{\sigma}(31)\cdot\vec{p}_{q_1} \vec{\sigma}(42)\cdot\vec{p}_{\bar q_4}\vec{\sigma}(42)}{8m_{q_1}m_{q_3}} \\ &\quad+ \displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{q_3}\vec{\sigma}(31)\cdot \vec{\sigma}(42)\vec{\sigma}(42)\cdot\vec{p}_{\bar q_2}}{8m_{q_1}m_{q_3}} +\displaystyle\frac{\vec{\sigma}(31)\cdot\vec{p}_{q_3}\vec{\sigma}(31)\vec{\sigma}(42) \cdot\vec{p}_{\bar q_4}\vec{\sigma}(42)}{8m^{2}_{q_3}} \\ &\quad-\left. \displaystyle\frac{\vec{\sigma}(42)\cdot\vec{p}_{\bar q_4}\vec{\sigma}(31)\cdot \vec{\sigma}(42)\vec{\sigma}(42)\cdot\vec{p}_{\bar q_2}}{8m_{q_1}m_{q_3}} -\displaystyle \frac{\vec{\sigma}(31)\cdot\vec{p}_{q_3}\vec{\sigma}(31)\cdot \vec{\sigma}(42)\vec{\sigma}(31)\cdot\vec{p}_{q_1}}{8m_{q_1}m_{q_3}}\right] .\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;(16) \end{split} $

To carry out the Fierz transformations, quark 3 (antiquark 4) and quark 1 (antiquark 2) must have the same flavor. Then, quark and antiquark masses possess
$m_{q_3}=m_{q_1}$ and$m_{\bar{q}_4}=m_{\bar{q}_2}$ . For convenience we use$\vec{p}_{q_1}^{\prime}=\vec{p}_{q_3}$ and$\vec{p}_{\bar{q}_2}^{\prime}=\vec{p}_{\bar{q}_4}$ . The Hamiltonian corresponding to the left diagram in Fig. 1 is$ \begin{split} H_1 =& V_{aq_{1}\bar{q}_{2}F}(\vec{k})+V_{q_1\bar{q}_1} +V_{q_2\bar{q}_2} + \sqrt {m^2_{q_1}+\vec{p}^{2}_{q_1}} +\sqrt {m^2_{\bar{q}_1}+\vec{p}^{2}_{\bar{q}_1}} +\sqrt {m^2_{q_2} +\vec{p}^{2}_{q_2}} +\sqrt {m^2_{\bar{q}_2}+\vec{p}^{2}_{\bar{q}_2}}, \end{split} $

(17) where
$V_{q_1\bar{q}_1}$ and$V_{q_2\bar{q}_2}$ are the Fourier transforms of$V_{ab}(\vec{r})$ in Eq. (9). The total spin of the two mesons is$ \vec{S}=\vec{S}_{q_1}+\vec{S}_{\bar{q}_1}+\vec{S}_{q_2}+\vec{S}_{\bar{q}_2} . $

(18) The commutator of the
$z$ component$S_z$ of the total spin and the Hamiltonian is$ \begin{split} &[S_z, H_1] = -\displaystyle\frac{g^{2}_s}{k^2} \displaystyle\frac{1}{8m^{2}_{q_1}} \left(\displaystyle\frac{1}{3}\lambda^{0}_{q_1f}\lambda^{0}_{\bar{q}_2f} +\displaystyle\frac{1}{2}\vec{\lambda}_{q_1f}\cdot\vec{\lambda}^{T}_{\bar {q}_2f}\right) \left(\displaystyle\frac{4}{9}\lambda^{0}_{q_1}\lambda^{0}_{\bar{q}_2} -\displaystyle\frac{1}{12}\vec{\lambda}_{q_1}\cdot\vec{\lambda}^{T}_{\bar {q}_2}\right) \times \{\sigma_{\bar {q}_{2}y}[p'_{\bar {q}_{2}z}p_{\bar {q}_{2}y}-p'_{\bar {q}_{2}y}p_{\bar {q}_{2}z}-p_{q_{1}y}p_{\bar {q}_{2}z}+ p_{q_{1}z}p_{\bar {q}_{2}y}\\ &\quad+p_{q_{1}y}p'_{\bar {q}_{2}z} -p_{q_{1}z}p'_{\bar {q}_{2}y}-p'_{q_{1}y}p_{\bar {q}_{2}z} + p'_{q_{1}z}p_{\bar {q}_{2}y}+p'_{q_{1}y}p'_{\bar {q}_{2}z} -p'_{q_{1}z}p'_{\bar{q}_{2}y}+p'_{q_{1}z}p_{q_{1}y}-p'_{q_{1}y}p_{q_{1}z}] + \sigma_{\bar {q}_{2}x}[p'_{\bar {q}_{2}z}p_{\bar {q}_{2}x}-p'_{\bar {q}_{2}x}p_{\bar {q}_{2}z}-p_{q_{1}x}p_{\bar {q}_{2}z}\\ &\quad+p_{q_{1}z}p_{\bar {q}_{2}x}+p_{q_{1}x}p'_{\bar {q}_{2}z} -p_{q_{1}z}p'_{\bar {q}_{2}x}-p'_{q_{1}x}p_{\bar {q}_{2}z} + p'_{q_{1}z}p_{\bar {q}_{2}x}+p'_{q_{1}x}p'_{\bar {q}_{2}z} -p'_{q_{1}z}p'_{\bar{q}_{2}x}+p'_{q_{1}z}p_{q_{1}x}-p'_{q_{1}x}p_{q_{1}z}] + \sigma_{q_{1}y}[p'_{q_{1}z}p_{q_{1}y}-p'_{q_{1}y}p_{q_{1}z} \\ &\quad-p_{q_{1}z}p_{\bar {q}_{2}y}+p_{q_{1}y}p_{\bar {q}_{2}z}-p_{q_{1}z}p'_{\bar {q}_{2}y} +p_{q_{1}y}p'_{\bar {q}_{2}z}+p'_{q_{1}z}p_{\bar {q}_{2}y} -p'_{q_{1}y}p_{\bar {q}_{2}z}+p'_{q_{1}z}p'_{\bar {q}_{2}y} -p'_{q_{1}y}p'_{\bar {q}_{2}z}+p'_{\bar {q}_{2}z}p_{\bar {q}_{2}y}-p'_{\bar {q}_{2}y}p_{\bar {q}_{2}z}] + \sigma_{q_{1}x}[p'_{q_{1}z}p_{q_{1}x}\\ &\quad-p'_{q_{1}x}p_{q_{1}z} -p_{q_{1}z}p_{\bar {q}_{2}x}+p_{q_{1}x}p_{\bar {q}_{2}z}-p_{q_{1}z}p'_{\bar {q}_{2}x} +p_{q_{1}x}p'_{\bar {q}_{2}z}+p'_{q_{1}z}p_{\bar {q}_{2}x} -p'_{q_{1}x}p_{\bar {q}_{2}z}+p'_{q_{1}z}p'_{\bar {q}_{2}x} -p'_{q_{1}x}p'_{\bar {q}_{2}z} +p'_{\bar {q}_{2}z}p_{\bar {q}_{2}x}-p'_{\bar {q}_{2}x}p_{\bar {q}_{2}z}] \\ &\quad + i\sigma_{q_{1}x}\sigma_{\bar {q}_{2}z}[-3p_{q_{1}y}p_{\bar {q}_{2}z} +p_{q_{1}y}p'_{\bar {q}_{2}z}+p'_{q_{1}y}p_{\bar {q}_{2}z}-3p'_{q_{1}y}p'_{\bar {q}_{2}z}-p_{q_{1}z}p_{\bar {q}_{2}y}+p'_{q_{1}z}p_{\bar {q}_{2}y} + p_{q_{1}z}p'_{\bar{q}_{2}y}-p'_{q_{1}z}p'_{\bar {q}_{2}y} +p'_{\bar {q}_{2}y}p_{\bar {q}_{2}z} +p'_{\bar {q}_{2}z}p_{\bar {q}_{2}y}\\ &\quad+p'_{q_{1}z}p_{q_{1}y} +p'_{q_{1}y}p_{q_{1}z}] + i\sigma_{q_{1}y}\sigma_{\bar {q}_{2}z}[3p_{q_{1}x}p_{\bar {q}_{2}z}-p_{q_{1}x}p'_{\bar {q}_{2}z}-p'_{q_{1}x}p_{\bar {q}_{2}z}+3p'_{q_{1}x}p'_{\bar {q}_{2}z} +p_{q_{1}z}p_{\bar {q}_{2}x}-p_{q_{1}z}p'_{\bar {q}_{2}x} -p'_{q_{1}z}p_{\bar{q}_{2}x}+p'_{q_{1}z}p'_{\bar {q}_{2}x} \\ &\quad-p'_{\bar {q}_{2}z}p_{\bar {q}_{2}x}-p'_{\bar {q}_{2}x}p_{\bar {q}_{2}z}-p'_{q_{1}z}p_{q_{1}x}-p'_{q_{1}x}p_{q_{1}z}] + i(\sigma_{q_{1}x}\sigma_{\bar {q}_{2}y} +\sigma_{q_{1}y}\sigma_{\bar {q}_{2}x}) [4p_{q_{1}x}p_{\bar {q}_{2}x}-4p_{q_{1}y}p_{\bar {q}_{2}y}-2p_{q_{1}x}p'_{\bar {q}_{2}x}+2p_{q_{1}y}p'_{\bar {q}_{2}y} \\ &\quad-2p'_{q_{1}x}p_{\bar{q}_{2}x} +2p'_{q_{1}y}p_{\bar {q}_{2}y} +4p'_{q_{1}x}p'_{\bar {q}_{2}x}-4p'_{q_{1}y}p'_{\bar {q}_{2}y} -2p'_{\bar {q}_{2}x}p_{\bar {q}_{2}x} +2p'_{\bar {q}_{2}y}p_{\bar {q}_{2}y} -2p'_{q_{1}x}p_{q_{1}x}+2p'_{q_{1}y}p_{q_{1}y}] + i(\sigma_{q_{1}y}\sigma_{\bar {q}_{2}y} \\ &\quad-\sigma_{q_{1}x}\sigma_{\bar {q}_{2}x}) [4p_{q_{1}y}p_{\bar{q}_{2}x}+4p_{q_{1}x}p_{\bar {q}_{2}y}-2p_{q_{1}y}p'_{\bar {q}_{2}x}-2p_{q_{1}x}p'_{\bar {q}_{2}y} -2p'_{q_{1}y}p_{\bar{q}_{2}x}-2p'_{q_{1}x}p_{\bar {q}_{2}y} +4p'_{q_{1}y}p'_{\bar {q}_{2}x}+4p'_{q_{1}x}p'_{\bar {q}_{2}y} -2p'_{\bar {q}_{2}y}p_{\bar {q}_{2}x}\\ &\quad-2p'_{\bar {q}_{2}x}p_{\bar{q}_2y} -2p'_{q_{1}y}p_{q_{1}x}-2p'_{q_{1}x}p_{q_{1}y}] + i\sigma_{q_{1}z}\sigma_{\bar {q}_{2}y}[3p_{q_{1}z}p_{\bar {q}_{2}x}-p_{q_{1}z}p'_{\bar {q}_{2}x}-p'_{q_{1}z}p_{\bar {q}_{2}x}+3p'_{q_{1}z}p'_{\bar {q}_{2}x}+p_{q_{1}x}p_{\bar {q}_{2}z}-p_{q_{1}x}p'_{\bar {q}_{2}z} \\ &\quad-p'_{q_{1}x}p_{\bar{q}_{2}z}+p'_{q_{1}x}p'_{\bar {q}_{2}z} -p'_{\bar {q}_{2}z}p_{\bar {q}_{2}x}-p'_{\bar {q}_{2}x}p_{\bar {q}_{2}z} -p'_{q_{1}z}p_{q_{1}x}-p'_{q_{1}x}p_{q_{1}z}] + i\sigma_{q_{1}z}\sigma_{\bar {q}_{2}x}[-3p_{q_{1}z}p_{\bar {q}_{2}y}+p_{q_{1}z}p'_{\bar {q}_{2}y} +p'_{q_{1}z}p_{\bar {q}_{2}y}\\ &\quad-3p'_{q_{1}z}p'_{\bar {q}_{2}y}-p_{q_{1}y}p_{\bar {q}_{2}z} +p_{q_{1}y}p'_{\bar {q}_{2}z} + p'_{q_{1}y}p_{\bar{q}_{2}z}-p'_{q_{1}y}p'_{\bar {q}_{2}z} +p'_{\bar {q}_{2}z}p_{\bar {q}_{2}y}+p'_{\bar {q}_{2}y}p_{\bar {q}_{2}z} +p'_{q_{1}z}p_{q_{1}y}+p'_{q_{1}y}p_{q_{1}z}]\}, \end{split} $

(19) where
$p_{ix}$ ,$p_{iy}$ , and$ p_{iz}$ are the three components of the momentum of incoming quark$i$ ($i=q_1, \bar{q}_2$ );$p'_{ix}$ ,$p'_{iy}$ , and$p'_{iz}$ are the three components of the momentum of outgoing quark$i$ ($ i=q_1, \bar{q}_2 $ );$\sigma_{q_1x}$ ,$\sigma_{q_1y}$ , and$\sigma_{q_1z}$ are the three components of$\vec{\sigma}_{q_1} \equiv \vec{\sigma}(31)$ ;$\sigma_{\bar{q}_2x}$ ,$\sigma_{\bar{q}_2y}$ , and$\sigma_{\bar{q}_2z}$ are the three components of$\vec{\sigma}_{\bar{q}_2} \equiv \vec{\sigma}(42)$ ;$\lambda^0_{q_1f} \equiv \lambda^0_f(31)$ ,$\lambda^0_{\bar{q}_2f} \equiv \lambda^0_f(42)$ ,$\vec{\lambda}_{q_1f} \equiv \vec{\lambda}_f(31)$ ,$\vec{\lambda}_{\bar{q}_2f} \equiv \vec{\lambda}_f(42)$ ,$\lambda^0_{q_1} \equiv \lambda^0(31)$ ,$\lambda^0_{\bar{q}_2} \equiv \lambda^0(42)$ ,$\vec{\lambda}_{q_1} \equiv \vec{\lambda}(31)$ , and$\vec{\lambda}_{\bar{q}_2} \equiv \vec{\lambda}(42)$ . Applying the momentum conservation$\vec{p}_{\bar{q}_2}^{\prime}=\vec{p}_{q_1} +\vec{p}_{\bar{q}_2}-\vec{p}_{q_1}^{\prime}$ , we obtain$ \begin{split} &[S_z, H_1] = -\displaystyle\frac{g^{2}_s}{k^2} \displaystyle\frac{1}{8m^{2}_{q_1}} \left(\displaystyle\frac{1}{3}\lambda^{0}_{q_1f}\lambda^{0}_{\bar{q}_2f} +\displaystyle\frac{1}{2}\vec{\lambda}_{q_1f}\cdot\vec{\lambda}^{T}_{\bar {q}_2f}\right) \left(\displaystyle\frac{4}{9}\lambda^{0}_{q_1}\lambda^{0}_{\bar{q}_2} -\displaystyle\frac{1}{12}\vec{\lambda}_{q_1}\cdot\vec{\lambda}^{T}_{\bar {q}_2}\right) \times \{\sigma_{\bar {q}_{2}y}[p'_{q_{1}y}p_{q_{1}z}+p'_{q_{1}y}p_{\bar {q}_{2}z} -p'_{q_{1}z}p_{q_{1}y}-p'_{q_{1}z}p_{\bar {q}_{2}y}+p_{\bar{q}_{2}y}p_{q_{1}z}\\ &\quad -p_{\bar {q}_{2}z}p_{q_{1}y}] + \sigma_{\bar {q}_{2x}}[p'_{q_{1}x}p_{q_{1}z}+p'_{q_{1}x}p_{\bar {q}_{2}z}-p'_{q_{1}z}p_{q_{1}x}-p'_{q_{1}z}p_{\bar {q}_{2}x}+p_{\bar {q}_{2}x}p_{q_{1}z}-p_{\bar {q}_{2}z}p_{q_{1}x}] + \sigma_{q_{1}y}[p'_{q_{1}z}p_{q_{1}y}-p'_{q_{1}y}p_{q_{1}z}-p_{q_{1}z}p_{\bar {q}_{2}y}+p'_{q_{1}z}p_{\bar {q}_{2}y}\\ &\quad+p_{q_{1}y}p_{\bar {q}_{2}z}-p'_{q_{1}y}p_{\bar {q}_{2}z}] + \sigma_{q_{1}x}[p'_{q_{1}z}p_{q_{1}x}-p'_{q_{1}x}p_{q_{1}z} -p_{q_{1}z}p_{\bar {q}_{2}x}+p'_{q_{1}z}p_{\bar {q}_{2}x}+p_{q_{1}x}p_{\bar {q}_{2}z}-p'_{q_{1}x}p_{\bar {q}_{2}z}] + i\sigma_{q_{1}x}\sigma_{\bar {q}_{2}z}[-p_{q_{1}y}p_{\bar {q}_{2}z}-3p'_{q_{1}y}p_{q_{1}z}\\ &\quad-3p'_{q_{1}y}p_{\bar {q}_{2}z}+4p'_{q_{1}y}p'_{q_{1}z}-p'_{q_{1}z}p_{\bar {q}_{2}y} + p_{q_{1}z}p_{\bar {q}_{2}y}+2p_{\bar {q}_{2}z}p_{\bar {q}_{2}y} +2p_{q_{1}y}p_{\bar {q}_{2}z}-p'_{q_{1}z}p_{q_{1}y}]+i\sigma_{q_{1}y}\sigma_{\bar {q}_{2}z}[p_{q_{1}x}p_{\bar {q}_{2}z} + 3p'_{q_{1}x}p_{q_{1}z}+3p'_{q_{1}x}p_{\bar {q}_{2}z}\\ &\quad-4p'_{q_{1}x}p'_{q_{1}z} +p'_{q_{1}z}p_{\bar {q}_{2}x}-p_{q_{1}z}p_{\bar {q}_{2}x}-2p_{\bar {q}_{2}z}p_{\bar {q}_{2}x} -2p_{q_{1}z}p_{q_{1}x}+p'_{\bar {q}_{2}z}p_{q_{1}x}] +i(\sigma_{q_{1}x}\sigma_{\bar {q}_{2}y}+\sigma_{q_{1}y}\sigma_{\bar {q}_{2}x})[4p'_{q_{1}x}p_{q_{1}x} +4p'_{q_{1}x}p_{\bar {q}_{2}x} \\ &\quad -4p'_{q_{1}x}p'_{q_{1}x}-4p'_{q_{1}y}p_{q_{1}y} -4p'_{q_{1}y}p_{\bar {q}_{2}y}+4p'_{q_{1}y}p'_{q_{1}y} +2p_{q_{1}y}p_{q_{1}y}-2p_{q_{1}x}p_{q_{1}x} + 2p_{\bar{q}_{2}y}p_{\bar {q}_{2}y}-2p_{\bar {q}_{2}x}p_{\bar {q}_{2}x}]\\ &\quad+i(\sigma_{q_{1}y}\sigma_{\bar {q}_{2}y} -\sigma_{q_{1}x}\sigma_{\bar {q}_{2}x}) [4p'_{q_{1}x}p_{q_{1}y}+4p'_{q_{1}x}p_{\bar {q}_{2}y} -8p'_{q_{1}x}p'_{q_{1}y}+4p'_{q_{1}y}p_{q_{1}x}+4p'_{q_{1}y}p_{\bar {q}_{2}x} -4p_{q_{1}x}p_{q_{1}y}-4p_{\bar {q}_{2}y}p_{\bar {q}_{2}x}]\\ &\quad +i\sigma_{q_{1}z}\sigma_{\bar {q}_{2}y}[p_{q_{1}z}p_{\bar {q}_{2}x} + 3p'_{q_{1}z}p_{q_{1}x} +3p'_{q_{1}z}p_{\bar {q}_{2}x}-4p'_{q_{1}z}p'_{q_{1}x}+p'_{q_{1}x}p_{\bar {q}_{2}z} +p'_{q_{1}x}p_{q_{1}z}-p_{q_{1}x}p_{\bar {q}_{2}z} -2p_{\bar {q}_{2}x}p_{\bar {q}_{2}z}-2p_{q_{1}x}p_{q_{1}z}]\\ &\quad +i\sigma_{q_{1}z}\sigma_{\bar {q}_{2}x}[-p_{q_{1}z}p_{\bar {q}_{2}z}-3p'_{q_{1}z}p_{q_{1}y}-3p'_{q_{1}z}p_{\bar{q}_{2}y} + 4p'_{q_{1}z}p'_{q_{1}y}-p'_{q_{1}y}p_{\bar {q}_{2}z} -p'_{q_{1}y}p_{q_{1}z}+2p_{q_{1}z}p_{q_{1}y}+2p_{\bar {q}_{2}y}p_{\bar {q}_{2}z}+p_{q_{1}y}p_{\bar {q}_{2}z}]\} .\quad\quad\quad\quad(20) \end{split} $

Replacing the subscripts,
$x$ in Eq. (20) with$y$ ($z$ ),$y$ with$z$ ($x$ ), and$z$ with$x$ ($y$ ), we obtain$[S_x, H_1]$ ($[S_y, H_1]$ ). Clearly,$[S_x, H_1]$ ,$[S_y, H_1]$ , and$[S_z, H_1]$ may not be zero. Therefore,$S_x$ ,$S_y$ , and$S_z$ may not be conserved, and hence, the total spin may not be conserved, i.e., the total spin of the two final mesons may not equal the total spin of the two initial mesons.For the right diagram in Fig. 1, the quark-antiquark potential corresponding to
$\bar q_1+q_2 \to q_3 + \bar q_4$ is between$q_2$ and$\bar{q}_1$ ,$ \begin{split} &\!\!\!\!\!\!\!V_{aq_2\bar{q}_1F}(\vec{k}) = -\displaystyle \frac{g^{2}_s}{k^2}\left[\displaystyle \frac{1}{3}\lambda^{0}_{f}(32)\lambda^{0}_{f}(41) +\displaystyle \frac{1}{2}\vec{\lambda}_{f}(32)\cdot\vec{\lambda}^{T}_{f}(41)\right] \times \left[\frac{4}{9}\lambda^{0}(32)\lambda^{0}(41)-\displaystyle \frac{1}{12} \vec{\lambda}(32)\cdot\vec{\lambda}^{T}(41)\right] \left[-\displaystyle \frac{3}{2}-\frac{1}{2}\vec{\sigma}(32)\cdot\vec{\sigma}(41) \right.\\ &\;\;+ \displaystyle \frac{\vec{\sigma}(41)\cdot\vec{p}_{{\bar q_4}}\vec{\sigma}(41)\cdot \vec{p}_{{{\bar q_1}}}}{8m_{q_2}m_{q_3}} +\displaystyle \frac{\vec{\sigma}(32)\cdot\vec{p}_{q_3}\vec{\sigma}(32)\cdot \vec{p}_{q_2}}{8m_{q_2}m_{q_3}} +\displaystyle \frac{3\vec{\sigma}(32)\cdot\vec{p}_{q_2} \vec{\sigma}(41)\cdot \vec{p}_{\bar{q}_1}}{8m^{2}_{q_2}} -\displaystyle \frac{\vec{\sigma}(32)\cdot\vec{p}_{q_2} \vec{\sigma}(41)\cdot \vec{p}_{\bar q_4}}{8m_{q_2}m_{q_3}} -\displaystyle \frac{\vec{\sigma}(32)\cdot\vec{p}_{q_3} \vec{\sigma}(41)\cdot \vec{p}_{\bar q_1}}{8m_{q_2}m_{q_3}}\\ &\;\;+\displaystyle \frac{3\vec{\sigma}(32)\cdot\vec{p}_{q_3} \vec{\sigma}(41)\cdot \vec{p}_{\bar q_4}}{8m^{2}_{q_3}} + \displaystyle \frac{\vec{\sigma}(32)\vec{\sigma}(32)\cdot\vec{p}_{q_2} \vec{\sigma}(41) \vec{\sigma}(41)\cdot\vec{p}_{\bar q_1}}{8m^{2}_{q_2}} +\displaystyle \frac{\vec{\sigma}(32)\vec{\sigma}(32)\cdot\vec{p}_{q_2} \vec{\sigma}(41) \cdot\vec{p}_{\bar q_4}\vec{\sigma}(41)}{8m_{q_2}m_{q_3}} \\ &\;\; + \displaystyle \frac{\vec{\sigma}(32)\cdot\vec{p}_{q_3}\vec{\sigma}(32)\cdot \vec{\sigma}(41)\vec{\sigma}(41)\cdot\vec{p}_{\bar q_1}}{8m_{q_2}m_{q_3}} +\displaystyle \frac{\vec{\sigma}(32)\cdot\vec{p}_{q_3}\vec{\sigma}(32)\vec{\sigma}(41) \cdot\vec{p}_{\bar q_4}\vec{\sigma}(41)}{8m^{2}_{q_3}} \\ &\;\;-\left. \displaystyle \frac{\vec{\sigma}(41)\cdot\vec{p}_{\bar q_4}\vec{\sigma}(32)\cdot \vec{\sigma}(41)\vec{\sigma}(41)\cdot\vec{p}_{\bar q_1}}{8m_{q_2}m_{q_3}} -\displaystyle \frac{\vec{\sigma}(32)\cdot\vec{p}_{q_3}\vec{\sigma}(32)\cdot \vec{\sigma}(41)\vec{\sigma}(32)\cdot\vec{p}_{q_2}}{8m_{q_2}m_{q_3}}\right] . \end{split} $

(21) To carry out the Fierz transformations, quark 3 (antiquark 4) and quark 2 (antiquark 1) must have the same flavor, and the quark and antiquark masses should satisfy
$m_{q_3}=m_{q_2}$ and$m_{\bar{q}_4}=m_{\bar{q}_1}$ . The Hamiltonian corresponding to the right diagram in Fig. 1 is$ \begin{split} H_2 = & V_{aq_2 \bar{q}_1F}(\vec{k})+V_{q_1\bar{q}_1} +V_{q_2\bar{q}_2} \\ & + \sqrt {m^2_{q_1}+\vec{p}^{2}_{q_1}} +\sqrt {m^2_{\bar{q}_1}+\vec{p}^{2}_{\bar{q}_1}} \\ &+\sqrt {m^2_{q_2}+\vec{p}^{2}_{q_2}} +\sqrt {m^2_{\bar{q}_2}+\vec{p}^{2}_{\bar{q}_2}} . \end{split} $

(22) We may obtain the commutator
$[S_z, H_2]$ from$[S_z, H_1]$ in Eq. (20) by the replacements$q_1 \leftrightarrow q_2$ and$\bar{q}_1 \leftrightarrow \bar{q}_2$ . We can also obtain$[S_x, H_2]$ and$[S_y, H_2]$ from$[S_x, H_1]$ and$[S_y, H_1]$ by the replacement.$[S_x, H_2]$ ,$[S_y, H_2]$ , and$[S_z, H_2]$ may not be zero. This indicates that$S_x$ ,$S_y$ , and$S_z$ may not be conserved, and hence, the total spin may not be conserved, i.e., the total spin of the two final mesons may not equal the total spin of the two initial mesons.The development in spherical harmonics of the relative-motion wave function of mesons
$A$ and$B$ (aside from a normalization constant) is given by$ \begin{split} {\rm e}^{\rm i\vec{p}_{q_1\bar{q}_1, q_2\bar{q}_2} \cdot \vec{r}_{q_1\bar{q}_1, q_2\bar{q}_2}} = & 4\pi \displaystyle\sum\limits_{L_{\rm i}=0}^{\infty} \displaystyle\sum\limits_{M_{\rm i}=-L_{\rm i}}^{L_{\rm i}} i^{L_{\rm i}} j_{L_{\rm i}} (\mid \vec{p}_{q_1\bar{q}_1, q_2\bar{q}_2} \mid r_{q_1\bar{q}_1, q_2\bar{q}_2}) \\ & \times Y_{L_{\rm i}M_{\rm i}}^\ast (\hat{p}_{q_1\bar{q}_1, q_2\bar{q}_2}) Y_{L_{\rm i}M_{\rm i}} (\hat{r}_{q_1\bar{q}_1, q_2\bar{q}_2}). \end{split} $

(23) The development of the relative-motion wave functionof mesons
$C$ and$D$ (aside from a normalization constant) is$ \begin{split} \!\!\!\!\!{\rm e}^{\rm i\vec{p}_{q_3\bar{q}_1, q_2\bar{q}_4} \cdot \vec{r}_{q_3\bar{q}_1, q_2\bar{q}_4}} = & 4\pi \displaystyle\sum\limits_{L_{\rm f}=0}^{\infty} \displaystyle\sum\limits_{M_{\rm f}=-L_{\rm f}}^{L_{\rm f}} i^{L_{\rm f}} j_{L_{\rm f}} (\mid \vec{p}_{q_3\bar{q}_1, q_2\bar{q}_4} \mid r_{q_3\bar{q}_1, q_2\bar{q}_4}) \\ & \times Y_{L_{\rm f}M_{\rm f}}^\ast (\hat{p}_{q_3\bar{q}_1, q_2\bar{q}_4}) Y_{L_{\rm f}M_{\rm f}} (\hat{r}_{q_3\bar{q}_1, q_2\bar{q}_4}), \end{split} $

(24) in
${\cal M}_{aq_1\bar {q}_2}$ , and$ \begin{split} \!\!\!\!\!{\rm e}^{\rm i\vec{p}_{q_1\bar{q}_4, q_3\bar{q}_2} \cdot \vec{r}_{q_1\bar{q}_4, q_3\bar{q}_2}} = & 4\pi \sum\limits_{L_{\rm f}=0}^{\infty} \sum\limits_{M_{\rm f}=-L_{\rm f}}^{L_{\rm f}} i^{L_{\rm f}} j_{L_{\rm f}} (\mid \vec{p}_{q_1\bar{q}_4, q_3\bar{q}_2} \mid r_{q_1\bar{q}_4, q_3\bar{q}_2}) \\ & \times Y_{L_{\rm f}M_{\rm f}}^\ast (\hat{p}_{q_1\bar{q}_4, q_3\bar{q}_2}) Y_{L_{\rm f}M_{\rm f}} (\hat{r}_{q_1\bar{q}_4, q_3\bar{q}_2}), \end{split} $

(25) in
${\cal M}_{ a\bar{q}_1q_2}$ .$Y_{LM}(\hat{r})$ are the spherical harmonics with the orbital-angular-momentum quantum number$L$ and the magnetic quantum number$M$ , and$\hat{r}$ denotes the polar angles of$\vec{r}$ . Let$S$ ($S^\prime$ ) and$S_z$ ($S_z^\prime$ ) be the total spin of mesons$A$ ($C$ ) and$B$ ($D$ ) and its$z$ component, respectively. In the transition amplitudes we have$ \begin{split} Y_{L_iM_i}\chi_{S_AS_{Az}}\chi_{S_BS_{Bz}} = & \displaystyle\sum\limits_{S=\mid S_A-S_B \mid}^{S_A+S_B} \displaystyle\sum\limits_{S_z=-S}^{S} (S_AS_{Az}S_BS_{Bz} \mid SS_z) \\ & \times \displaystyle\sum\limits_{J=\mid L_i-S \mid}^{L_i+S} \displaystyle\sum\limits_{J_z=-J}^{J} (L_iM_iSS_z \mid JJ_z) \varphi_{JJ_z}^i, \end{split} $

(26) $ \begin{split} \!\!\!\!\!\!Y_{L_fM_ f}\chi_{S_CS_{Cz}}\chi_{S_DS_{Dz}} =& \!\! \displaystyle\sum\limits_{S^\prime =\mid S_C-S_D \mid}^{S_C+S_D} \displaystyle\sum\limits_{S_z^\prime =-S^\prime}^{S^\prime} (S_CS_{Cz}S_DS_{Dz} \mid S^\prime S_z^\prime) \\ & \times \displaystyle\sum\limits_{J^\prime=\mid L_f -S^\prime \mid}^{L_f+S^\prime} \displaystyle\sum\limits_{J_z^\prime=-J^\prime}^{J^\prime} (L_fM_fS^\prime S_z^\prime \mid J^\prime J_z^\prime) \varphi_{J^\prime J_z^\prime}^ f, \end{split} $

(27) where the Clebsch-Gordan coefficients are used. The spherical harmonics and the spin wave functions are coupled to the wave functions
$\varphi_{JJ_z}^ i$ and$\varphi_{J^\prime J_z^\prime}^ f$ , where$J$ ($J^\prime$ ) is the total angular-momentum quantum number of the two initial (final) mesons, and$J_z$ ($J_z^\prime$ ) is its$z$ component. Even though the total spin of the two final mesons may not be equal to the total spin of the two initial mesons in the reactions listed in Table 1, the total angular momentum of the two final mesons equals the total angular momentum of the two initial mesons. In addition, parity is conserved. The parity conservation connects the orbital-angular-momentum quantum numbers in the relative-motion wave functions of the initial and final mesons. The orbital-angular-momentum quantum numbers are selected to satisfy the parity conservation, symmetrization of wave functions of identical bosons, and$J=J^\prime$ . For example,$L_i=L_ f=J$ excluding$L_i=L_f=0$ is required in$K\bar{K} \to K\bar{K}^*$ ,$K\bar{K} \to K^*\bar{K}$ ,$\pi K \to \pi K^*$ ,$\pi K \to \rho K$ , and$\pi \rho \to K\bar{K}$ ;$L_i=L_f=J$ with$L_i>0$ , odd$L_i$ for$I=1$ , and even$L_i$ for$I=0$ in$\pi \pi \to K\bar{K}^*$ and$\pi \pi \to K^* \bar{K}$ . In practical calculations, the summations over$L_ i$ in Eq. (23) and over$L_ f$ in Eqs. (24) and (25) are from 0 to 3.Channel ${{\cal M}_{aq_1\bar{q}_2f}}$ 

${{\cal M}_{a\bar{q}_1 q_2f}}$ 

${I=1 \; K \bar {K} \to K \bar {K}^\ast}$ 

0 1 ${I=0 \; K \bar {K} \to K \bar {K}^\ast}$ 

2 1 ${I=1 \; K \bar {K} \to K^* \bar {K}}$ 

0 1 ${I=0 \; K \bar {K} \to K^* \bar {K}}$ 

2 1 ${I=3/2 \; \pi K \to \pi K^\ast}$ 

0 0 ${I=1/2 \; \pi K \to \pi K^\ast}$ 

0 ${\displaystyle\frac{3}{2}}$ 

${I=3/2 \; \pi K \to \rho K}$ 

0 0 ${I=1/2 \; \pi K \to \rho K}$ 

0 ${\displaystyle\frac{3}{2}}$ 

${I=1 \; \pi \pi \to K \bar{K}^\ast}$ 

0 −1 ${I=0 \; \pi \pi \to K \bar{K}^\ast}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; \pi \pi \to K^* \bar{K}}$ 

0 −1 ${I=0 \; \pi \pi \to K^* \bar{K}}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; \pi \pi \to K^* \bar{K}^*}$ 

0 −1 ${I=0 \; \pi \pi \to K^* \bar{K}^*}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; \pi \rho \to K \bar {K}}$ 

0 −1 ${I=0 \; \pi \rho \to K \bar {K}}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; \pi \rho \to K^* \bar {K}^*}$ 

0 −1 ${I=0 \; \pi \rho \to K^* \bar {K}^*}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; \rho \rho \to K^\ast \bar {K}^*}$ 

0 −1 ${I=0 \; \rho \rho \to K^\ast \bar {K}^*}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; K \bar {K}^* \to \rho \rho}$ 

0 −1 ${I=0 \; K \bar {K}^* \to \rho \rho}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

${I=1 \; K^* \bar {K} \to \rho \rho}$ 

0 −1 ${I=0 \; K^* \bar {K} \to \rho \rho}$ 

0 ${-\displaystyle\frac {\sqrt 6}{2}}$ 

Table 1. Flavor matrix elements.
-
From the transition potential and the mesonic quark-antiquark relative-motion wave functions, we calculated the unpolarized cross sections for the 2-to-2 meson-meson reactions that arise from quark-antiquark annihilation and creation in the first Born approximation. The following reactions were studied:
$K \bar {K} \to K \bar {K}^\ast $ ,$ K\bar{K} \to K^\ast \bar{K}$ ,$\pi K \to \pi K^\ast$ ,$\pi K \to \rho K$ ,$\pi \pi \to K \bar{K}^\ast$ ,$\pi \pi \to K^* \bar K$ ,$\pi \pi \to K^\ast\bar{K}^\ast$ ,$\pi \rho \to K \bar{K}$ ,$\pi \rho \to K^\ast\bar{K}^\ast$ ,$\rho \rho \to K^\ast\bar{K}^\ast$ ,$K \bar{K}^\ast \to \rho \rho$ , and$K^* \bar{K} \to \rho \rho$ . The Hamiltonian of the two mesons contains the quark-antiquark potential, which is equivalent to the transition potential. We derived the commutation relations of the total spin of the two mesons and the Hamiltonian. Owing to the quark-antiquark potential, the commutators may not be zero, and the total spin may not be conserved in the reactions. As the center-of-mass energy of the two initial mesons increases from the threshold energy, the cross sections for the endothermic reactions increase very rapidly to the peak cross sections first, and then decrease or display plateaus for$\pi \pi \to K^\ast\bar{K}^\ast$ and$\pi \rho \to K^\ast\bar{K}^\ast$ at some temperatures. The cross sections exhibit remarkable temperature dependence. To use the cross sections conveniently, we parametrized the numerical cross sections for the ten isospin channels of reactions. Based on the flavor matrix elements, the cross sections for the other isospin channels of reactions can be obtained from the cross sections for the ten channels.
Cross sections for inelastic 2-to-2 meson-meson scattering in hadronic matter
- Received Date: 2018-08-27
- Accepted Date: 2018-10-27
- Available Online: 2019-02-01
Abstract: With quark-antiquark annihilation and creation in the first Born approximation, we study the reactions:





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























 DownLoad:
DownLoad: