-
Due to their large masses, heavy flavors have unique advantages in both experimental and theoretical studies of quantum chromodynamics (QCD). Since
$ J/\psi $ was initially proposed as a probe of the deconfined matter known as “quark-gluon plasma” (QGP) [1], its anomalous yield suppression through parton scattering and enhancement from the recombination of charm and anti-charm quarks in QGP have been widely studied in experiments [2–5] and theoretical models [6–12]. Charmonium is produced by an initial hard-scattering process referred to as “primordial production”, which occurs in hadronic collisions with spectator nucleons [13]. Charmonium states are assumed to form before QGP reaches local equilibrium, they then undergo inelastic scatterings and color screening effects when moving through QGP, which results in dissociations and also transitions between different eigenstates ($ J/\psi $ ,$ \psi^{\prime} $ ,$ \chi_c $ ) [14–20]. These eigenstates are finally detected in experiments through their decay into dileptons. At LHC energies, abundant charm pairs are produced in nuclear collisions, this significantly enhances the probability of c and$ \bar c $ combining to generate new$ J/\psi $ s in the QGP [21–23], in a process called “regeneration”. As most charm quarks are distributed in low and middle$ p_{\rm T} $ regions, the regeneration process dominates the nuclear modification factor and the collective flows of$ J/\psi $ in the low and middle$ p_{\rm T} $ bins [24]. In the high$ p_{\rm T} $ bin, charmonia are mainly produced from the initial hadronic collisions [10].More experimental data about the charmonium excited state
$ \psi(2S) $ has been measured in$ \sqrt{s_{\rm NN}} = 2.76 $ TeV [25] and 5.02 TeV [26] Pb-Pb collisions, across different centralities and transverse momentum bins. The ratio$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ has been measured for these two collision energies, and there is considerable discrepancy between the values reported. At 2.76 TeV,$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ becomes larger than unity in the most central collisions when$ 3<p_{\rm T}<30 $ GeV/c. At 5.02 TeV, the ratio is$ \sim 0.5 $ in a similar centrality and momentum bin. Both sets of experimental data feature large error bars, which prevents any solid conclusions being drawn. In contrast to$ J/\psi $ ,$ \psi(2S) $ is a loosely bound state. Its wavefunction is significantly modified by the high-temperature medium, which can obscure its dissociation and regeneration rates. Having a smaller binding energy,$ \psi(2S) $ is thermally produced more frequently in the lower temperature region than$ J/\psi $ , and inherits larger collective flows from the bulk medium [17, 27, 28]. This sequential regeneration can affect the$ p_{\rm T} $ dependence of the ratio$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ .In this paper, a two-component transport model is employed to study both
$ J/\psi $ and$ \psi(2S) $ production in different centralities and momentum bins for$ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions. The decay rates of excited states are updated with a more realistic formula instead of employing a survival temperature$ T_d $ above which no charmonia can survive. This improvement can explain effectively the ratio of$ \psi(2S)/J/\psi $ in 5.02 TeV Pb-Pb collisions. The rest of this paper proceeds as follows. In Sec. 2, the details of an improved Boltzmann transport model for charmonium evolution, and the hydrodynamic equations for QGP expansion, are introduced. In Sec. 3, realistic calculations for$ J/\psi $ and$ \psi(2S) $ in$ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions are performed and the results are compared with experimental data. A final summary is given in Sec. 4. -
Heavy quarkonium evolution in phase-space has, though the use of Boltzmann transport models, been well-studied for hot deconfined mediums in the SPS [9] and LHC [29, 30], for both p-Pb and Pb-Pb collisions. Focusing on hot-medium effects, one can start quarkonium evolutions after their production in hard-scattering processes. The three-dimensional transport equation for charmonium evolution is simplified as,
$ \left[\cosh(y-\eta){\frac{\partial}{\partial\tau}}+{\frac{\sinh(y-\eta)}{\tau}}{\frac{\partial}{\partial \eta}}+{\bf v}_{\rm T}\cdot\nabla_{\rm T}\right]f_{\Psi} = -\alpha_{\Psi} f_{\Psi}+\beta_{\Psi}, $

(1) $ f_{\Psi} $ is the Ψ phase-space density. y and η are the rapidities in momentum and coordinate space, respectively.$ { v}_{\rm T} = { p}_{\rm T}/E_{\rm T} = { p}_{\rm T}/\sqrt{m_{\Psi}^2+p_{\rm T}^2} $ is the transverse velocity of charmonium, which represents the leakage effects for a cooling system with finite size, i.e., charmonia with large velocities tend to escape from the thermal medium instead of dissociating. Primordially-produced charmonia in the initial hadronic collisions suffer color screening effects and parton inelastic scatterings, which are both included in the decay rate$ \alpha_{\Psi} $ ,$ \alpha_{\Psi} = {1\over E_{\rm T}} \int {{\rm d}^3{ k}\over {(2\pi)^3E_{\rm g}}}\sigma_{{\rm g}\Psi}({ p},{ k},T)F_{{\rm g}\Psi}({ p},{ k})f_{\rm g}({ k},T), $

(2) where
$ E_{\rm g} $ and$ f_{\rm g} $ are gluon energy and density in the thermal medium, respectively.$ F_{{\rm g}\Psi} $ is the flux factor. In the expanding QGP,$ u^\mu $ represents the four-velocity of the fluid. The gluonic Ψ cross-section in a vacuum is extracted from the perturbative calculation with a Coulomb potential approximation. For the thermal medium, this paper takes a similar approach to Ref. [9], using a reduced charmonium binding energy of the form,$ \sigma_{{\rm g}\Psi}(w) = A_0 {(w/\epsilon_{\Psi}-1)^{3/2}\over (w/\epsilon_{\Psi})^5} $

(3) with
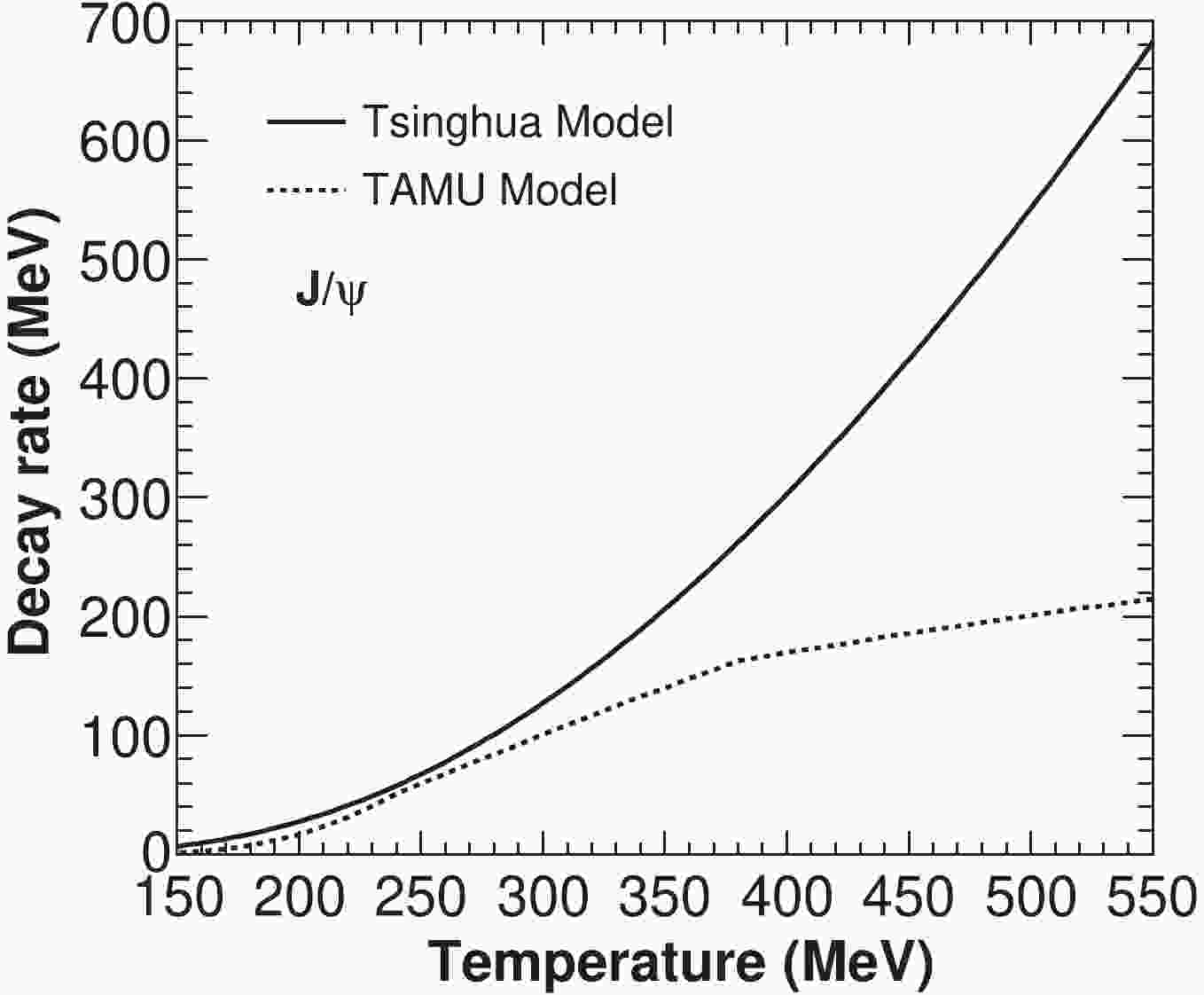
$ A_0 = (2^{11}\pi/27)(m_c^3\epsilon_{\Psi})^{-1/2} $ and$ \epsilon_{\Psi} $ representing the binding energy of Ψ. The charm quark mass is taken as the mass of a D meson, to fit the binding energy of charmonium in a vacuum.$ w = p_{\Psi}^\mu p_{{\rm g}\mu}/m_{\Psi} $ is the gluon energy in the Ψ rest-frame. In Fig.1, the$ J/\psi $ decay rate$ \alpha_{\Psi} $ is compared with the quasi-free dissociation rate [27]. Most$ J/\psi $ s can survive in the relatively low temperature region, and two different transport models of the decay rate present similar final results for the region$ T<300 $ MeV, where most QGP and charmonia are located [7, 30].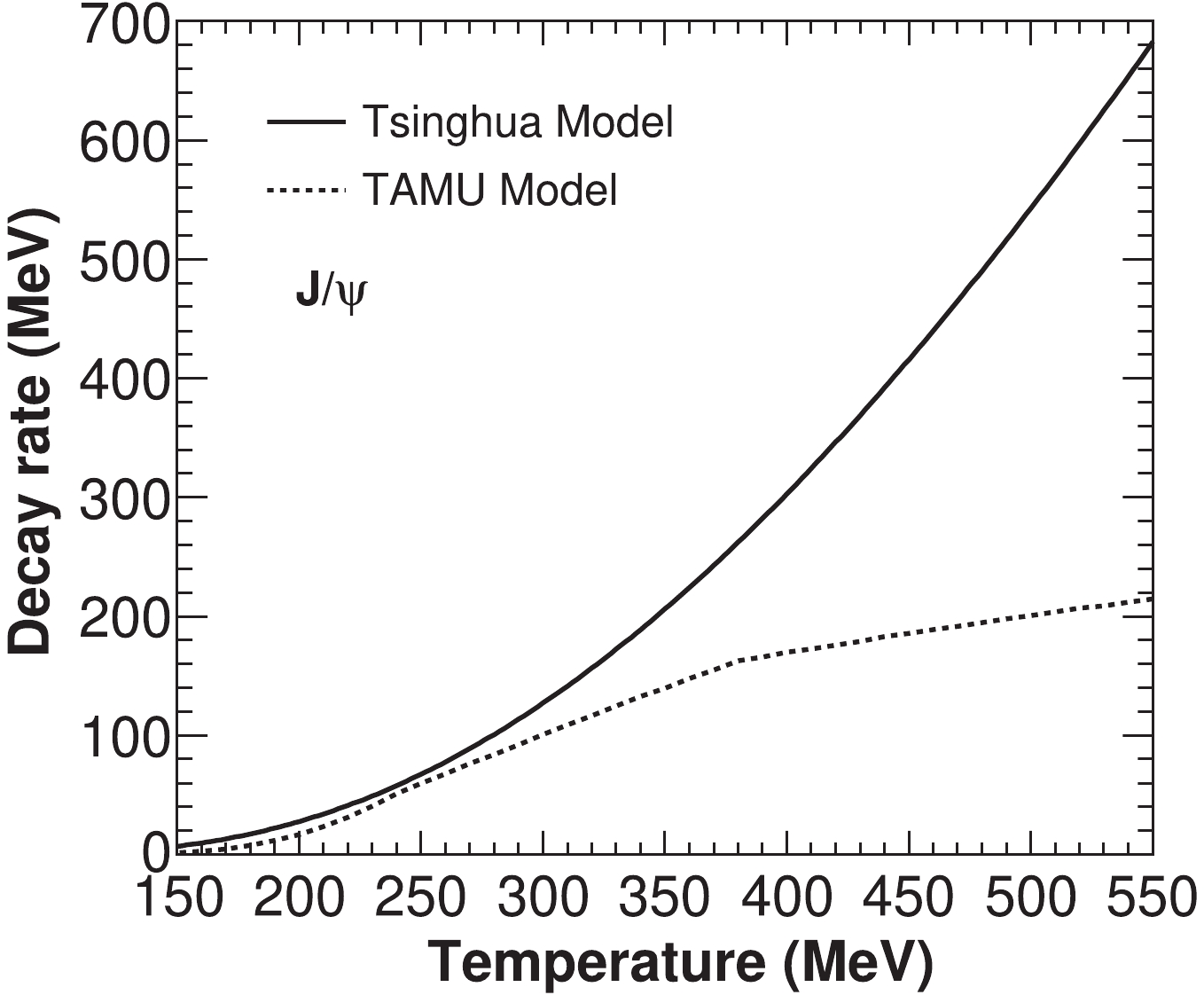
Figure 1.
$ J/\psi $ decay rate in the thermal medium as a function of temperature T. The decay rate from quasi-free dissociation is shown for comparison. The solid line is from the improved version of the transport model, developed by TSINGHUA Group [9, 10, 31], and the dotted line is from the calculations of TAMU Group [6, 7, 27].The heavy quark potential
$ V(r,T) $ can be partially screened by the thermal medium, especially at the large distances and high temperatures suggested by lattice QCD calculations [32]. Charmonium bound states may disappear sequentially in the static medium. The maximum survival temperature of a certain bound state is called the "dissociation temperature"$ T_{\rm d} $ , above this the bound state disappears. In nuclear collisions, the assumption that no bound states survive at$ T>T_{\rm d} $ strongly suppresses the$ \psi(2S) $ production, where no excited states can survive inside the QGP at$ T>T_{\rm d}^{\chi_c,\psi(2S)}\approx 1.1T_{\rm c} $ . Similarly to fast cooling systems, charmonium states might survive in the region$ T>T_{\rm d} $ if the medium quickly cools down to below$ T_{\rm d} $ . In this work, the approximation of$ \alpha_{\Psi}(T>T_{\rm d}) = +\infty $ employed in [33] is replaced by a large but finite value, shown in Fig.1. The new decay rate increases the survival probability of excited states, and weakly affects the production of$ J/\psi $ s due to their large$ T_{\rm d} $ . The$ \psi(2S) $ decay rate is extracted from the nuclear geometry scale,$ \alpha_{\psi(2S)} = \alpha_{J/\psi}\times \langle r\rangle^2_{\psi(2S)}/\langle r\rangle^2_{J/\psi} $ , and$ \chi_c $ is found in a similar way. The mean radius of charmonia in a vacuum is calculated with the potential model$ \langle r\rangle_{J/\psi, \chi_c,\psi(2S)} = (0.5, 0.72, 0.9) $ fm [14].At LHC energies, many charm pairs are also produced in Pb-Pb collisions, which can significantly increase the recombination of uncorrelated charm and anti-charm quarks in the QGP. This process is included in Eq.(1) by the term
$ \beta_{\Psi} $ . The regeneration rate depends on both charm and anti-charm quark densities in the QGP, and also their recombination probability. At high temperatures, charmonium binding energies are reduced significantly, which suppresses the regeneration probability of charmonium. As$ \psi(2S) $ s are loosely bound, they are thermally produced in the hadronization of QGP. Charm quarks with color charges strongly couple with the QGP and lose energy. In relativistic heavy ion collisions, large quench factors and collective flows for charmed mesons have been observed [34–36]. Therefore, one can approximately take the kinetically thermalized phase-space distribution for charm quarks as being at$ \tau\geqslant \tau_0 $ , where$ \tau_0 $ is the time-scale of the QGP local equilibrium [37]. As heavy quarks are rarely produced in the thermal medium due to their large masses, the total number of charm pairs is conserved with spatial diffusions inside the QGP [38]. The spatial density is controlled by the conservation equation.$ \partial_{\mu}(\rho_{\rm c}u^\mu) = 0. $

(4) The initial charm quark density at
$ \tau_0 $ is obtained from nuclear geometry,$ \rho_c({ x}_{\rm T}, \eta,\tau_0) = {{{\rm d}\sigma_{\rm pp}^{c{\bar c}}} \over {\rm d}\eta}{ T_A({ x}_{\rm T})T_B({ x}_{\rm T}-{ b})\cosh(\eta)\over \tau_0}, $

(5) where
$ T_A $ and$ T_B $ are the thickness functions of two colliding nuclei, with the definition$ T_{A(B)}({ x}_{\rm T}) = $ $ \int_{-\infty}^{\infty} {\rm d}z\rho_{A(B)}({ x}_{\rm T},z) $ .$ \rho_{A(B)}({ x}_{\rm T},z) $ is understood to be the Woods-Saxon nuclear density. The rapidity distribution of charm pairs in$ \sqrt{s_{\rm NN}} = 5.02 $ TeV pp collisions is obtained by interpolation of the experimental data for 2.76 TeV and 7 TeV collisions,$ {\rm d}\sigma_{\rm pp}^{c\bar c}/{\rm d}y = 0.86 $ mb in the central rapidity region$ |y|<0.9 $ , and 0.56 mb in the forward rapidity region$ 2.5<|y|<4 $ [39].The momentum distribution of charmonium primordially produced in A-A collisions is scaled from its distribution in pp collisions. The parametrization of the charmonium initial distribution at 5.02 TeV is similar to the form it takes at 2.76 TeV,
$ {{\rm d}^2\sigma_{{\rm pp}}^{J/\psi}\over {\rm d}y2\pi p_{\rm T}{\rm d}p_{\rm T}} = f_{J/\psi}^{\rm{Norm}}(p_{\rm T}|y) \cdot {{\rm d}\sigma_{{\rm pp}}^{J/\psi}\over {\rm d}y}, $

(6) $ f_{J/\psi}^{\rm{Norm}}(p_{\rm T}|y) = {(n-1)\over {\pi(n-2)\langle p_{\rm T}^2\rangle_{\rm pp}}} \left[1+{p_T^2\over {(n-2)\langle p_{\rm T}^2\rangle_{\rm pp}}}\right]^{-n}. $

(7) The charmonium rapidity differential cross-section at 5.02 TeV is
$ {\rm d}\sigma_{\rm pp}^{J/\psi}/{\rm d}y = $ 5.0 µb in the central rapidity$ |y|<1 $ , and 3.25 µb in the forward rapidity$ 2.5<|y|<4 $ , these were found through an interpolation between the experimental results for 2.76 TeV [40] and 7 TeV [41] pp collisions.$ f_{J/\psi}^{\rm{Norm}}(p_{\rm T}|y) $ is the normalized transverse momentum distribution of charmonium with rapidity y. The mean squared transverse momentum$ \langle p_{\rm T}^2\rangle $ and the parameter n are calculated as$ \langle p_{\rm T}^2\rangle_{\rm pp}|_{y = 0} = 12.5\ {\rm{(GeV/c)^2}} $ and$ n = 3.2 $ . For the charmonium momentum distribution in other rapidities, which have less constraints,$ \langle p_{\rm T}^2\rangle_{\rm pp}(y) $ is determined by the relation,$ \langle p_{\rm T}^2\rangle_{\rm pp}^{J/\psi}(y) = \langle p_{\rm T}^2\rangle_{\rm pp}^{J/\psi}|_{y = 0}\times \left[1-\left({y\over y_{\rm{max}}}\right)^2\right], $

(8) where
$ y_{\rm{max}} = \cosh^{-1}(\sqrt{s_{\rm NN}}/(2E_{\rm T})) $ , and is the maximum rapidity of charmonium in pp collisions with zero transverse momentum. As the masses of charmonium excited states ($ \chi_c,\psi(2S) $ ) are similar to$ J/\psi $ s, their initial momentum distributions are approximated to be the same as those in Eqs.(6,7).In nuclear collisions, the charmonium initial distribution is also modified by shadowing effects in the nucleus [42, 43]. This paper employs the EPS09 NLO model [44] to generate the modification factors for primordially-produced charmonium in
$ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions. This suppression factor is$ \sim 0.8 $ depending on the impact parameter. For the regeneration, shadowing effects reduce the number of charm pairs by around 20%, and suppress the regeneration by a factor of$ \sim 0.8^2 $ .The expanding QGP background of charmonium evolution is simulated with the (2+1)-dimensional ideal hydrodynamic equations in the transverse plane, under the assumption of Bjorken expansion in the longitudinal direction.
$ \partial_{\mu} T^{\mu\nu} = 0 , $

(9) $ T^{\mu\nu} = (e+p)u^\mu u^\nu -g^{\mu\nu}p $ , and is the energy-momentum tensor. e and p are the energy density and pressure, respectively.$ u^\mu $ is the four-velocity of the QGP fluid, which can affect charm quark spatial diffusions through Eq.(4) as well as charmonium regeneration. It also determines the collective flows of light hadrons, charmed mesons and regenerated charmonia. The deconfined matter is treated as an ideal gas of massless gluons, u and d quarks and strange quarks with mass$ m_{\rm s} = 150 $ MeV [45]. Hadron gas is an ideal gas made up of all known hadrons and resonances with masses of up to 2 GeV [46]. The two phases are connected by a first-order phase transition with a critical temperature of$ T_{\rm c} = 170 $ MeV. The initial maximum temperature of the QGP is calculated as$ T_0({ x}_{rm T} = 0, \tau_0) = 510 $ MeV in the central rapidity$ |y|<2.4 $ , and 450 MeV in the forward rapidity$ 2.5<|y|<4 $ . Here$ \tau_0 = 0.6 $ fm/c, and is the time-scale for the QGP to reach local equilibrium [37]. The lifetime of QGP is$ \sim 10 $ fm/c for the most central Pb-Pb collisions at$ \sqrt{s_{\rm NN}} = 5.02 $ TeV. -
With the transport model for charmonium evolution and the hydrodynamic equations for QGP collective expansion, one can obtain realistic nuclear modification factors for charmonia in heavy ion collisions. In the left-hand panel of Fig.2, primordially-produced charmonia undergo dissociations from peripheral to central Pb-Pb collisions, shown with the dotted line. The regeneration process
$ c+\bar c \rightarrow J/\psi +g $ is plotted with the dashed line and is proportional to the number of charm quark pairs in the QGP, it dominates total$ J/\psi $ production in central collisions. The experimental data in the left-hand panel of Fig.2 is inclusive production; it includes the non-prompt contribution from B hadron decays, which contributes around 10% of the final inclusive yield. The detailed momentum dependence of the non-prompt fraction in$ J/\psi $ inclusive production is fitted as$f_B = N_{\rm pp}^{B\rightarrow J/\psi}/ (N_{\rm pp}^{\rm{prompt}}+$ $ N_{\rm pp}^{B\rightarrow J/\psi}) = 0.04+0.023p_{\rm T}/({\rm GeV/c}) $ [33], with a weak dependence on the rapidity and colliding energy$ \sqrt{s_{\rm NN}} $ . In nuclear collisions, bottom quarks suffer strong energy losses in the thermal medium. B hadrons and non-prompt charmonia are shifted from high$ p_{\rm T} $ to relatively low$ p_{\rm T} $ . This hot medium modification of the non-prompt charmonium (or bottom quark) momentum distribution is characterized with a quench factor$ R_{\rm Q} $ . In high$ p_{\rm T} $ ,$ R_{\rm Q} $ is smaller than unity, and is calculated as 0.4 for the non-prompt$ J/\psi $ $ R_{AA} $ [33]. This value is employed in the entire$ p_{\rm T} $ region. With both prompt and non-prompt charmonia, one can obtain charmonium's inclusive nuclear modification factors, which are shown in Fig.2. Taking into account the large uncertainties of$ {\rm d}\sigma_{\rm pp}^{c\bar c}/{\rm d}y $ in the transport model, this paper performs two calculations for$ R_{AA} $ under a change in$ {\rm d}\sigma_{\rm pp}^{c\bar c}/{\rm d}y $ of ±20% (see the color band in Fig.2) . In most central collisions, primordial production is strongly suppressed and regeneration dominates the total yield.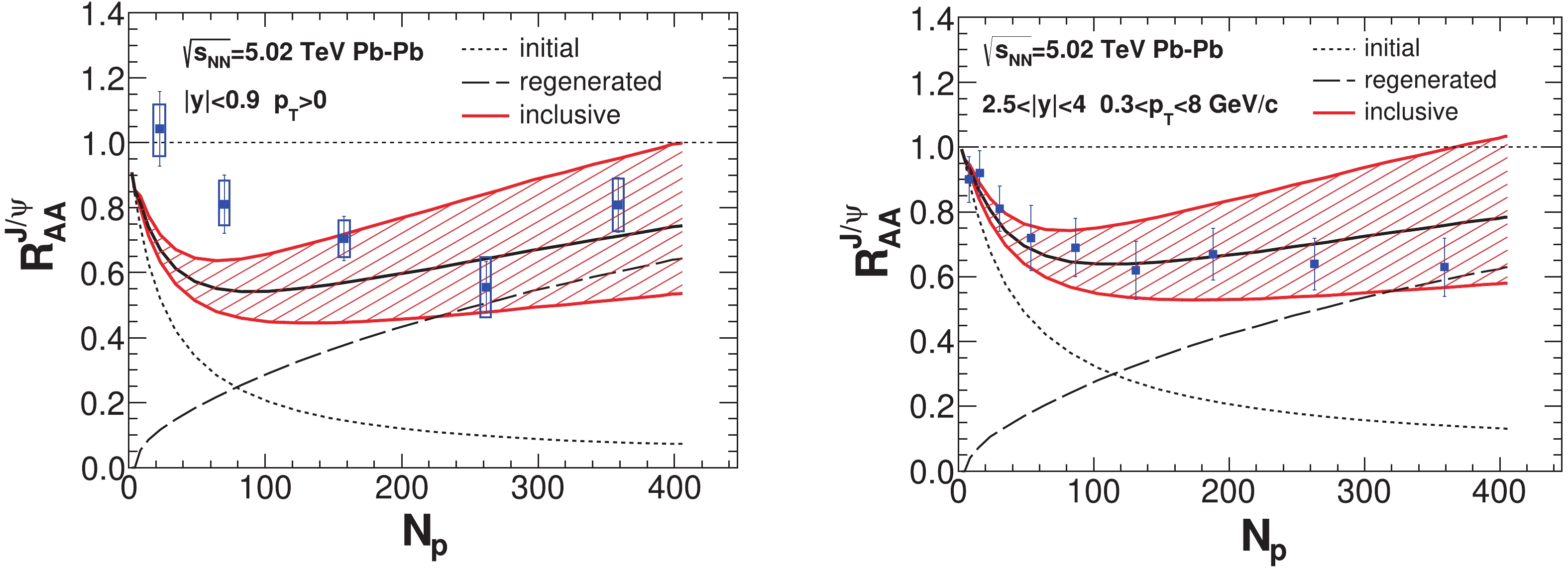
Figure 2. (color online) (left-hand panel) Inclusive nuclear modification factor
$ R_{AA} $ of$ J/\psi $ as a function of the number of participants$ N_{\rm p} $ in central rapidity for Pb-Pb collisions at$ \sqrt{s_{\rm NN}} = 5.02 $ TeV. The dotted and dashed lines represent primordial production and regeneration, respectively. The solid black line in the middle of the band is for$ J/\psi $ inclusive of$ R_{AA} $ . The color band is for the uncertainties of the inputs, with$ {\rm d}\sigma_{\rm pp}^{c\bar c}/{\rm d}y $ changed by ±20%. Experimental data is from the ALICE Collaboration [47]. (right-hand panel) Inclusive$ R_{AA} $ in forward rapidity. The lines and band are similar to the left panel. Experimental data is from ALICE Collaboration [48].In the forward rapidity, both initial conditions of the hydrodynamic equations and transport model are updated by comparison to the central rapidity collisions. In the right panel of Fig.2, the
$ J/\psi $ nuclear modification factor from primordial production (dotted line), regeneration (dashed line), and inclusive production (color band) are plotted separately. The flat tendency of the experimental data at larger$ N_{\rm p} $ is due to the combined effects of the decreased primordial production and increased regeneration in the final$ J/\psi $ yield. The experimental data in the right-hand panel of Fig.2 is plotted for the range$ 0.3<p_{\rm T}<8 $ GeV/c. This excludes the contribution from coherent photoproduction, which occurs below 0.3 GeV/c and can make the total$ R_{AA} $ larger than unity in ultra-peripheral collisions [31].In order to show the contributions of primordial production and regeneration, the
$ p_{\rm T} $ -differential$ R_{AA} $ is also plotted in the left-hand panel of Fig.3. The significant increase of$ R_{AA} $ in the low$ p_{\rm T} $ region is caused by regeneration, and its large suppression in the high$ p_{\rm T} $ region is due to the effects of color screening and the inelastic collisions of partons. The dotted line represents the initial production, and it increases slightly with$ p_{\rm T} $ due to the leakage effect. The theoretical results for$ R_{AA}^{J/\psi} $ in both central and forward rapidities can explain the experimental data well. Note that even the charm pair cross-section$ {\rm d}\sigma_{\rm pp}^{c\bar c}/{\rm d}y $ value is larger in a central rapidity than in a forward one,$ R_{AA} $ is similar across the two rapidities, because in a central rapidity with a hotter medium, the QGP strong expansion “blows” charm quarks to a larger volume, which suppresses the charm quark spatial density and the regeneration rate of charmonium. Meanwhile, the elliptic flows of regenerated charmonia become larger in the central rapidity. These will be discussed in detail below. In the right-hand panel of Fig.3, the contributions of prompt$ J/\psi $ and$ \psi(2S) $ to$ R_{AA} $ , as a function of rapidity, are also presented.
Figure 3. (color online) (left-hand panel)
$ J/\psi $ nuclear modification factor$ R_{AA} $ as a function of the transverse momentum$ p_{\rm T} $ . The dotted line represents initial production, and the solid line is the inclusive production comprising initial production, regeneration and B hadron decay. The color band is due to the uncertainties of$ {\rm d}\sigma_{\rm pp}^{c\bar c}/{\rm d}y $ (see Fig.2). The differences between the solid and dotted lines are mainly due to the contributions of regeneration at low$ p_{\rm T} $ and B hadron decay at high$ p_{\rm T} $ , respectively. Experimental data is from the ALICE Collaboration [49]. (right-hand panel) The contribution of prompt$ J/\psi $ towards$ R_{AA} $ as a function of rapidity in the centrality 0%-100%. Prompt$ \psi(2S) $ s contribution to$ R_{AA}(y) $ is also predicted. The experimental data is from [50].The situation is more complicated for
$ \psi(2S) $ in the hot medium, owing to its dissociation rate compared with the tightly bound$ J/\psi $ . The$ \psi(2S) $ decay rate here is extracted from$ J/\psi $ ' using the nuclear geometry scale of Sec. II. In Fig.4, charmonia at high$ p_{\rm T} $ mainly arise from the primordial production. In moving from peripheral to central collisions, the dissociation rate of$ \psi(2S) $ increases, and the ratio of$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ decreases with$ N_{\rm p} $ . In the most central collisions at LHC, the ratio of charmonium nuclear modification factors is proportional to their decay rates. In peripheral collisions, the charmonium path length in the hot medium becomes smaller. Under weak suppression, the$ J/\psi $ and$ \psi(2S) $ nuclear modification factors approach unity, which entails that$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi}\rightarrow 1 $ as$ N_{\rm {\rm p}}\rightarrow 2 $ , (see left-hand panel of Fig.4). The individual$ R_{AA}^{J/\psi} $ in the high$ p_{\rm T} $ bin is also plotted in the right-hand panel of Fig.4. The decreasing tendencies of$ J/\psi $ and$ \psi(2S) $ $ R_{AA} $ with increasing$ N_{\rm p} $ are explained well.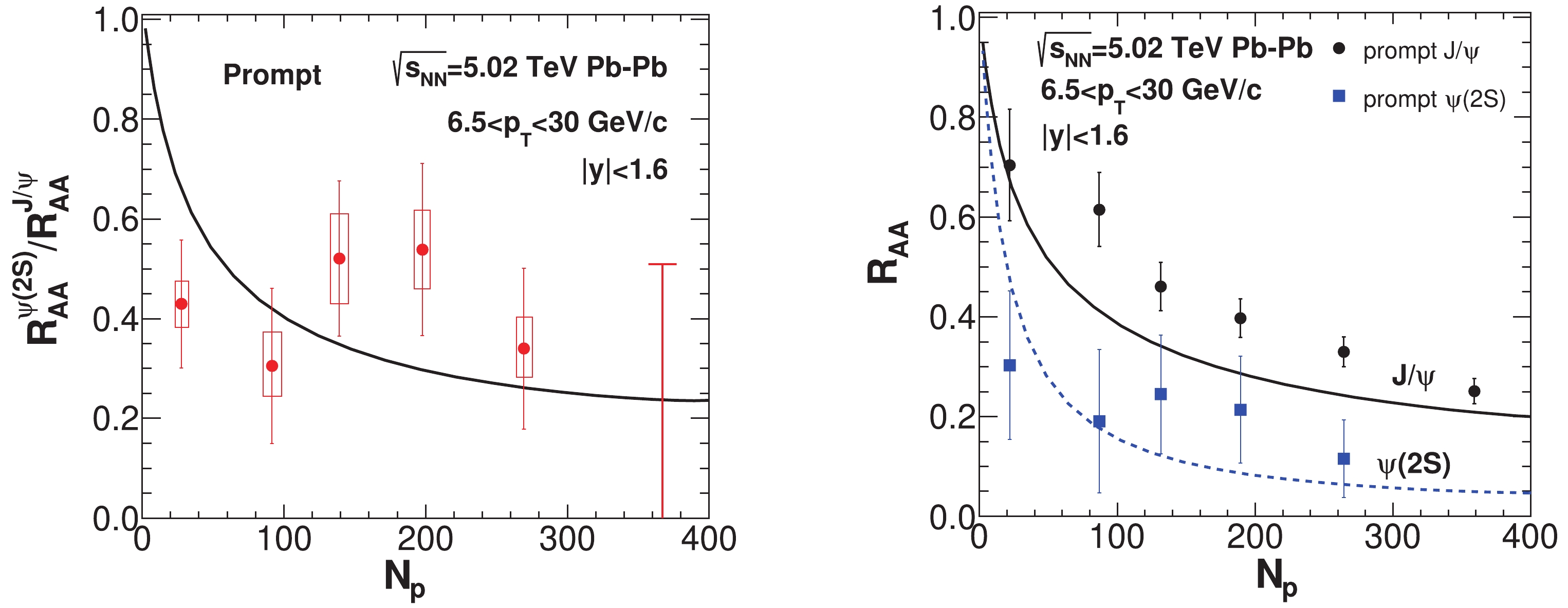
Figure 4. (color online) (left-hand panel) The ratio of
$ J/\psi $ and$ \psi(2S) $ prompt nuclear modification factors in the central rapidity region with momentum cut-offs of$ 6.5<p_{\rm T}<30 $ GeV/c for$ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions. Experimental data is from the CMS Collaboration [26]. (right-hand panel)$ J/\psi $ and$ \psi(2S) $ prompt nuclear modification factors as a function of$ N_{\rm p} $ in the central rapidity region with momentum cut-offs of$ 6.5<p_{\rm T}<30 $ GeV/c for$ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions. The experimental data is from [50].The transverse momentum dependence of
$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ is also studied via the sequential regeneration mechanism. In Fig.5, as$ p_{\rm T}\rightarrow 0 $ , there will be significant regeneration of$ J/\psi $ . The loosely-bound$ \psi(2S) $ can only be thermally produced in the later stages of QGP expansion compared with$ J/\psi $ , which leads to the production of regenerated$ \psi(2S) $ with larger velocities and collective flows inherited from the bulk medium, because of the strong couplings between the charm quarks and the deconfined medium. Therefore, the regenerated$ \psi(2S) $ are distributed at a larger$ p_{\rm T} $ (dashed line in right-hand panel of Fig.5) compared with the regenerated$ J/\psi $ . Due to the different$ p_{\rm T} $ distributions of the thermally produced$ J/\psi $ and$ \psi(2S) $ , the shapes of$ J/\psi $ and$ \psi(2S) $ $ R_{AA}(p_{\rm T}) $ s (solid black and blue lines in right-hand panel of Fig.5) are different. There is a "peak" in the ratio$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ in the left-hand panel of Fig.5 due to the sequential regeneration of$ \psi(2S) $ . In the absence of$ \psi(2S) $ regeneration, the ratio will decrease to zero as$ p_{\rm T}\rightarrow 0 $ (see the solid line in the left-hand panel of Fig.5.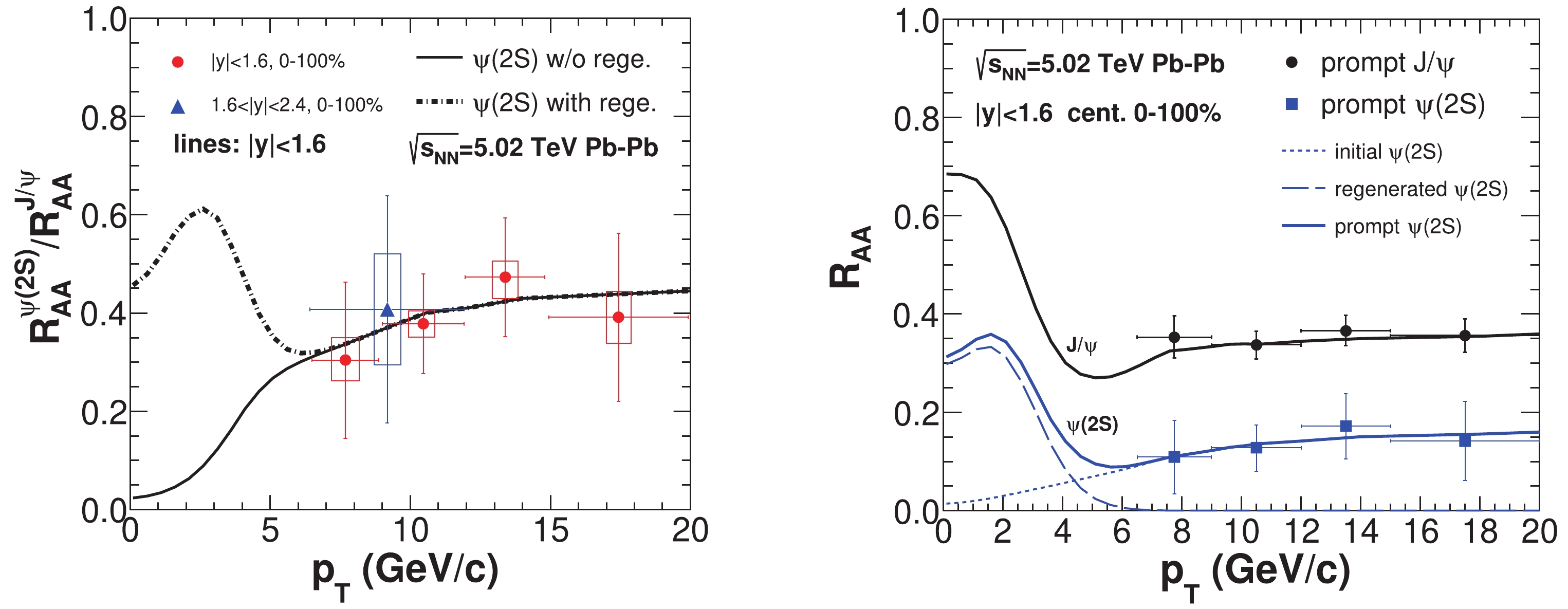
Figure 5. (color online) (left-hand panel) The ratio of the
$ J/\psi $ and$ \psi(2S) $ prompt nuclear modification factors as a function of the transverse momentum$ p_{\rm T} $ in the minimum bias (corresponding to the impact parameter b = 8.4 fm) for$ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions. Dotted-dashed and solid lines are with and without$ \psi(2S) $ regeneration, respectively. Experimental data is from the CMS Collaboration [26, 50]. (Right-hand panel) The$ J/\psi $ and$ \psi(2S) $ nuclear modification factors as a function of transverse momentum. Dotted, dashed and solid black lines are for initial, regenerated and prompt$ \psi(2S) $ , respectively. The prompt$ R_{AA}^{J/\psi} $ is also plotted for comparison. The experimental data is from [26, 50].In the low and middle
$ p_{\rm T} $ regions, regeneration becomes important for$ J/\psi $ and$ \psi(2S) $ , and enhances their$ R_{AA} $ in semi-central and central collisions. In order to show the role of$ \psi(2S) $ regeneration on$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ , this study presents two calculations with and without$ \psi(2S) $ regeneration, respectively, in Fig.6. In Fig.6, neglecting the regeneration of$ \psi(2S) $ (solid line),$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ continues to decrease with$ N_{\rm p} $ due to the stronger QGP suppression of charmonium excited states. The contribution of regeneration increases$ \psi(2S) $ production, most notably in the central collisions, and enhances the value of$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ (see the dotted-dashed line). Note that in Ref. [33], predictions about prompt$ R_{AA}^{\psi(2S)}/R_{AA}^{J/\psi} $ in 2.76 TeV Pb-Pb collisions have been made. Its value is predicted to be around$ \sim 0.15 $ in all$ p_{\rm T} $ bins. The binding energy and regeneration rate for$ \psi(2S) $ in Ref. [33] are smaller, which suppresses the$ \psi(2S) $ production. In this study these calculations are extended from 2.76 TeV [33] to 5.02 TeV, and both calculations are consistent with the experimental data at 5.02 TeV. The difference between the solid and dotted-dashed lines in Fig.6 is due to the$ \psi(2S)$ regeneration component.
Figure 6. (color online) Ratio of the
$ J/\psi $ and$ \psi(2S) $ prompt nuclear modification factors as a function of$ N_{\rm p} $ in rapidity$ 1.6<|y|<2.4 $ with momentum cut-offs of$ 3<p_{\rm T}<30 $ GeV/c. The dotted-dashed line represents the scenario for$ J/\psi $ and$ \psi(2S) $ with both primordial production and regeneration, and the solid line is the scenario without regeneration for$ \psi(2S) $ ($ J/\psi $ regeneration is included in both lines). Experimental data at$ \sqrt{s_{\rm NN}} = 2.76 $ TeV and 5.02 TeV is from the CMS Collaboration [26].Furthermore, the anisotropies of the
$ J/\psi $ and$ \psi(2S) $ momentum distributions are shown in Fig.7. Charmonia moving inside the QGP are likely to be in a color-neutral bound state, thus they are weakly coupled with the bulk medium, and less affected by the collective expansion of the QGP compared with unbound charm quarks. The non-zero elliptic flow of primordially-produced$ J/\psi $ at$ p_{\rm T}>6 $ GeV/c is mainly due to the effects of path length differences in the transverse plane (see the solid line in the left-hand panel of Fig.7). At low$ p_{\rm T} $ ,$ J/\psi $ production is dominated by the regeneration component. These heavy quarks are strongly coupled with the thermal medium and inherit collective flows, which results in a peak of$ v_2 $ at$ p_{\rm T}\sim 3 $ GeV/c. The elliptic flows of the prompt$ \psi(2S) $ are also displayed as a dotted line. As$ \psi(2S) $ are regenerated in the later stages of QGP anisotropic expansion, their elliptic flow is larger than that of$ J/\psi $ '. In the high$ p_{\rm T} $ region, the momentum anisotropy of$ \psi(2S) $ is larger than that of$ J/\psi $ ', as they are easily dissociated and sensitive to the anisotropy of the bulk medium.
Figure 7. (color online) (left-hand panel) The elliptic flows of the prompt
$ J/\psi $ and$ \psi(2S) $ as a function of the transverse momentum$ p_{\rm T} $ in centrality 20%-40% for the forward rapidity$ 2.5<|y|<4 $ $ \sqrt{s_{\rm NN}} = 5.02 $ TeV Pb-Pb collisions. Solid and dotted lines are used for the prompt$ J/\psi $ and$ \psi(2S) $ , respectively. (right-hand panel) The elliptic flows of inclusive$ J/\psi $ as a function of the transverse momentum$ p_{\rm T} $ . The solid and dotted lines represent the inclusive$ J/\psi $ in forward and central rapidities, respectively. Experimental data is from the ALICE Collaboration [51].In the right-hand panel of Fig.7 the experimental data is for the inclusive
$ J/\psi $ , and includes a non-prompt contribution from the B hadron decay. The solid line represents the inclusive$ J/\psi $ , assuming the kinetic equilibrium for bottom quarks as the upper limit [30]. The non-prompt contribution becomes important at high$ p_{\rm T} $ and therefore the kinetically thermalized bottom quarks can enhance the inclusive$ v_2^{J/\psi} $ by$ \sim 2 $ % at$ p_{\rm T}\sim 8 $ GeV/c.$ v_2^{J/\psi} $ in central rapidity is also calculated and shown as a dotted line for comparison. The situation for inclusive$ \psi(2S) $ is connected with the energy loss of bottom quarks in QGP, and has been comprehensively studied in Ref. [33]. -
In summary, this work employs an improved transport model to study the thermal production of
$ J/\psi $ and$ \psi(2S) $ in Pb-Pb collisions at$ \sqrt{s_{\rm NN}} = 5.02 $ TeV. Charmonium nuclear modification factors are dominated by regeneration at low$ p_T $ and primordial production at high$ p_{\rm T} $ , respectively. With different binding energies,$ J/\psi $ and$ \psi(2S) $ can be sequentially produced in the different stages of QGP anisotropic expansion, resulting in different$ p_{\rm T} $ distributions of the regenerated$ J/\psi $ and$ \psi(2S) $ . This explains well both the$ J/\psi $ and$ \psi(2S) $ $ R_{AA} $ s and their ratio in 5.02 TeV Pb-Pb collisions, and clearly shows how the open charm quark evolution can affect the final charmonium production. The sequential regeneration of$ J/\psi $ and$ \psi(2S) $ describes the charm quark diffusion histories and QGP expansion in heavy-ion collisions.I acknowledge instructive discussions with Prof. Pengfei Zhuang and Jiaxing Zhao. I am also grateful to Prof. Carsten Greiner for the kind hospitality during this study.
Thermal production of charmonia in Pb-Pb collisions at ${ \sqrt{{ s}_{\bf{ {\rm NN}}}}{\bf {=5.02}}}$ TeV
- Received Date: 2019-07-09
- Available Online: 2019-12-01
Abstract: This work uses the Boltzmann transport model to study the thermal production of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: