-
The
$ np\to \pi^0\pi^0d $ reaction presents a sharp peak around$ 2370 $ MeV with a narrow width of approximately$ 70 $ MeV; this peak is also observed in the$ pp\to \pi^+\pi^-d $ reaction but with approximately double the strength [1–3]. In the absence of a conventional reaction mechanism that can explain the occurrence of these peaks, they have been interpreted as signals of a dibaryon labeled as$ d^*(2380) $ . Based on this hypothesis, other features observed in π production experiments and$ NN $ phase shifts have also been interpreted (see [4] for a recent review). Notably, the narrow peak in$ np\to \pi\pi d $ affects the inelasticity of the$ NN $ phase shifts and is expected to influence these$ NN $ phase shifts, as emphasized in [5, 6]. Previously, several mechanisms of the two pion production leading to$ \pi\pi d $ have been studied [1–3] based on the model reported in [7] for$ NN\to NN\pi\pi $ ; this system features double Δ production with subsequent$ \Delta\to \pi N $ decay or$ N^*(1440) $ production with the decay of$ N^* $ to$ N\pi\pi $ or$ N^*\to \pi\Delta(N\pi) $ . In all these cases, the resulting$ np $ particles are fused into a deuteron. However, the results of these calculations lead to cross sections with smaller strengths compared to the peak of the$ np\to \pi^0\pi^0d $ reaction and produce no peaks with the energy of the observed peak. Such conclusions have already been drawn in a previous study [8], and we explicitly recalculated the cross sections based on these mechanisms to corroborate all previous findings. Interestingly, in the same study [8], a peak with poor statistics, already visible for the$ np\to \pi^+\pi^-d $ reaction, was explained using a different mechanism, namely two step sequential π production$ np\to pp\pi^- $ followed by$ pp\to \pi^+d $ . The cross section for the$ np\to \pi^+\pi^-d $ reaction was evaluated by factorizing the cross sections for the two latter reactions based on an "on-shell" approach, which, however, required further tests for accuracy. Notably, such a mechanism has not been further invoked considering the availability of new improved data on the$ np\to \pi^+\pi^-d $ and$ np\to \pi^0\pi^0d $ reactions [1–3].Meanwhile, the time reversal reaction involved in
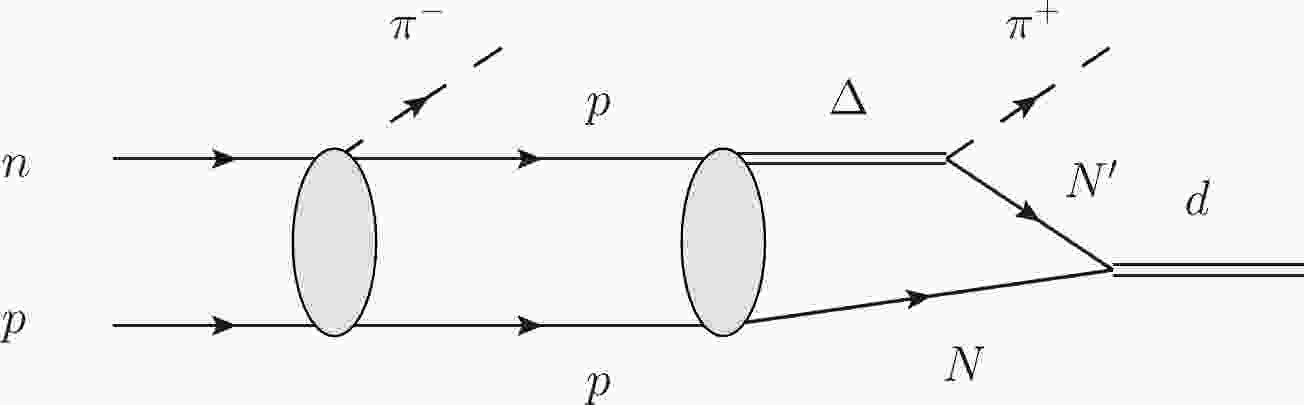
$ pp\to \pi^+d $ , that is,$ \pi^+ $ absorption in a deuteron,$ \pi^+d\to pp $ , has been studied in the past [9–11]. Such investigations have revealed that this reaction has a neat peak corresponding to the Δ excitation. Combining the results of previous studies [9–11] with the idea reported in [8] on the$ np\to \pi^+\pi^-d $ reaction, the mechanism underlying the$ np\to \pi^+\pi^-d $ reaction can be expressed diagrammatically, as shown in Fig. 1.After several years, the availability of more refined data and new theoretical developments suggest the need to revisit this issue based on the same idea:
$ 1) $ Recent data on$ np\to \pi^+\pi^-d $ and$ np\to \pi^0\pi^0 d $ have excellent precision [1–4].$ 2) $ The$ np\to \pi^0\pi^0d $ reaction involves$ \pi^0\pi^0 $ in isospin state$ I=0 $ , and hence, the inital$ np $ state must also be in state$ I=0 $ .In [3], the
$ np\to \pi^+\pi^-d $ reaction was split into$ I=0 $ and$ I=1 $ states, and as expected, the same peak visible for the$ np\to \pi^0\pi^0 d $ reaction was observed for the$ np\mathrm{(I=0)}\to \pi^+\pi^-d $ reaction with approximately double the strength. This implies that in the$ np\to \pi^-pp $ reaction, the first step of the sequential single pion production mechanism, i.e., the inital$ np $ state, is also in state$ I=0 $ . Recently, the first step, shown in Fig. 1 as$ np\to \pi^-pp $ with$ np $ in$ I=0 $ , has been singled out with a relatively good precision [12] (see revision about normalization in [12, 13]).$ 3) $ New developments concerning triangle singularities [14] facilitate our understanding of the high strength of the$ pp\to \pi^+d $ reaction with a triangle singularity, as depicted in the triangle diagram shown in the last section of Fig. 1. This corresponds to the simultaneous occurrence of Δ and two nucleons on shell and collinear. A simplification of the formalism on the triangle singularities, as accomplished in [15], allows immediate localization of the peak of the$ pp\to \pi^+d $ cross section based on Eq. (18) presented in [15]; here, the mass d is considered slightly unbound to determine a solution to the given equation. One predicts that a peak of the cross section should appear around$ M_{\mathrm{inv}}(pp)\sim 2179 $ MeV, which is very close to the location of the peak found in the experiment reported in [16]. The Coleman-Norton theorem [17] clarifies this case to visualize the process. The theorem states that a triangle singularity appears if the process visualized in the triangle diagram can occur at the classical level. In our case, this would occur as follows: the$ pp $ system produces$ \Delta N $ back to back in the$ pp $ rest frame; Δ decays into a$ \pi^+ $ along the direction of Δ and$ N' $ along the opposite direction, which is along the direction of N. Following this,$ N' $ moves faster than N (encoded by Eq. (18) in [15]) and approaches N to fuse into a deuteron. The fusion of the two nucleons into a deuteron occurs naturally when the discussed mechanism has a triangle singularity, producing a neat peak and a cross section that are notably large compared with those of typical fusion reactions [18]. We reanalyzed the$ pp\to \pi^+d $ reaction based on this new perspective [19]; however, corresponding details are nonessential for the derivation of the$ np\to\pi^+\pi^-d $ cross section, which, as reported in [8], relies on experimental cross sections, using the new$ np {(I=0)}\to \pi^-pp $ cross section [12, 13] and the data available for$ pp\to \pi^+d $ [16]. We also improved the on shell approach adopted in [8]. It is worth mentioning that while the mechanism for$ pp\to\pi^+d $ described in [9–11] could not be identified as a triangle singularity, the authors of [11] demonstrated that the cross section blew up when the Δ width was set to zero, a characteristic of the triangle singularity. In [19], the authors demonstrated that the dominant term in$ pp\to \pi^+d $ is the partial wave$ ^1D_2\,(^{2S+1}L_J) $ , which is in agreement with the experimental observations reported in [20]. Along similar lines, one may trace back$ J^P=1^+,3^+ $ for the$ d\pi^+\pi^- $ system, with some preference for$ 3^+ $ and$ ^3D_3 $ in the initial$ np $ system, i.e., the preferred quantum numbers associated with the$ d^*(2380) $ peak [4].It is also worth mentioning that the dominance of the
$ ^1D_2 $ partial wave leads to a structure indicative of a resonance in the$ pp\to \pi d $ reaction [21]: a dibaryon other than "$ d^*(2380) $ ." Theoretical groups also suggest bound states of$ N\Delta $ , three body$ \pi NN $ [22], or$ N\Delta $ [23] to explain the peak produced by this reaction; however, in [24], the authors could not prove adequate binding. In fact, as presented in [25], the Argand plots corresponding to a resonance and the triangle singularity are similar. We strictly follow the basic rule stating that if one phenomenon can be explained using conventional, well established facts, this interpretation should be favored over less conventional ones. Previous studies [9–11, 19] explaining the$ pp\to \pi d $ reaction on conventional grounds have proved that a new dibaryon is not essential to explain the foregoing reaction. -
The derivation of the
$ np\to \pi^+\pi^-d $ cross section follows the steps involved in the optical theorem [26]. Let us denote t as the amplitude for the isoscalar$ np {(I=0)}\to \pi^-pp $ reaction,$ t' $ as the amplitude for$ pp\to\pi^+d $ , and$ t^{\prime\prime} $ as the amplitude for$ np {(I=0)}\to \pi^+\pi^-d $ . The differential cross section for the isoscalar$ np {(I=0)}\to \pi^-pp $ reaction is given by$ \frac{{\rm d}\sigma_{np\to \pi^-pp}^I}{{\rm d} M_\mathrm{inv}(p_1p_1')}=\frac{1}{4ps}(2 M_N)^4\frac{1}{16\pi^3}p_\pi\tilde{p}_1|\bar{t}|^2\frac{1}{2}, $

(1) where
$ \sigma^I $ stands for the isoscalar cross section,$ \sqrt{s} $ is the center-of-mass (CM) energy of the inital$ np $ state,$ M_{\mathrm{inv}}(p_1p'_1) $ is the invariant mass of the final two protons involved in this reaction, p is the CM momentum of the inital n or p particles,$ p_\pi $ is the pion momentum in the$ np $ rest frame, and$ \tilde{p}_1 $ is the momentum of the final protons in the$ pp $ rest frame. We use the$ (2M_N)^4 $ factor of the fermion field normalization for nucleons following the formalism proposed by Mandl and Shaw [27]. The magnitude$ |\bar{t}|^2 $ indicates the angle averaged value of$ |t|^2 $ , and the factor$\dfrac{1}{2}$ considers the identity of the two final protons.Similarly, the cross section for
$ pp\to \pi^+d $ in the second part of the diagram of Fig. 1 is given by$ \sigma_{pp\to \pi^+d}=\frac{1}{16\pi M_{\mathrm{inv}}^2(p_1p_1')}\frac{p_\pi'}{\tilde{p}_1}|\bar{t}\,'|^2 (2M_N)^2(2M_d) , $

(2) where
$ p'_\pi $ is the$ \pi^+ $ momentum in the$ pp $ rest frame, and$ |\bar{t}'|^2 $ stands for angle averaged$ |t'|^2 $ . We choose to normalize the deuteron field in the form of nucleons, and we added a factor$ 2M_d $ (which disappears from the final formulas). Meanwhile, the amplitude for the$ np\to\pi^-\pi^+d $ process in Fig. 1 is given by$ \begin{aligned}[b] -{\rm i} t^{\prime\prime}=&\frac{1}{2}\int\frac{{\rm d}^4p_1}{(2\pi)^4}\frac{(2M_N)^2}{2E_N(p_1)2E_N(p'_1)}\frac{\rm i}{p_1^0-E_N(p_1)+{\rm i}\epsilon}\\&\times\frac{\rm i}{\sqrt{s}-p_1^0-\omega_\pi-E_N(p'_1)+{\rm i}\epsilon}\,(-{\rm i})t\,(-{\rm i})t' . \end{aligned} $

(3) Here, the factor
$ \dfrac{1}{2} $ accounts for the intermediate propagator of two identical particles. In the$ d^4p_1 $ integrations, t and$ t' $ would be off shell. In [8], the pion and two protons in the intermediate state were assumed to be on shell, and t and$ t' $ were used with the on shell variables. However, theoretical advances [28] allow us to proceed beyond this approximation. Indeed, the chiral unitary approaches reported in [28] for meson-meson interactions or in [29] for meson-baryon interactions factorize the vertices on-shell and perform a loop integral of the two intermediate states. A different justification has been provided in [30], wherein a dispersion relation is derived for the inverse of the hadron-hadron scattering amplitude. Another justification has been provided in [31, 32], wherein with the aid of chiral Lagrangians, the authors demonstrated that the off shell parts of the amplitudes appearing in the approach canceled with counterterms provided by the same theory. This implies that in Eq. (3), we can take$ tt' $ outside the$ dp_1^0 $ integral with the on-shell values and evaluate the remainder of the integral.On performing the
$ p_1^0 $ integration analytically with Cauchy's residues, we obtain$ \begin{aligned}[b] t^{\prime\prime}=&\frac{1}{2}\int\frac{{\rm d}^3p_1}{(2\pi)^3}\frac{(2M_N)^2}{2E_N(p_1)2E_N(p'_1)}\\&\times\frac{tt'}{\sqrt{s}-E_N(p_1)-E_N(p'_1)-\omega_\pi+{\rm i}\epsilon} , \end{aligned} $

(4) where
$ \vec{p}_1 $ ,$ \vec{p}_1\,' $ denote the momenta of the intermediate$ pp $ particles in Fig. 1, and$ \omega_\pi $ is the$ \pi^- $ energy. The$ t,t' $ amplitudes are Lorentz invariant, and we choose to evaluate the$\int \dfrac{{\rm d}^3p_1}{2E_1(p_1)}$ integral in the$ pp $ rest frame, where$|\vec{p}\,'_1|= |\vec{p}_1|$ and$ \sqrt{s}-\omega_\pi $ becomes the invariant mass of the two protons. This integral is logarithmically divergent and requires regularization. The result smoothly depends on a cut off$ p_{1,\mathrm{max}} $ for$ |\vec{p}_1| $ , which is used to regularize the$ d^3p_1 $ integral. We set some values for$ p_{1,\mathrm{max}} $ within a reasonable range. Despite this, we anticipate that the on shell part given by Eq. (5) below provides the largest contribution to the$ t''$ amplitude. Given that$ \tilde{p}_1= 552 $ MeV/c for$M_{{\rm inv}(p_1p_1')}= 2179$ MeV, the triangle singularity would appear for$ t' $ and Δ with a zero width or a pronounced peak when the width is considered; thus, values of$ p_{1,\mathrm{max}} $ around$ 700-800 $ MeV seem reasonable.The on-shell approximation used in [8] allows one to express the cross section for
$ np\to\pi^+\pi^-d $ in terms of the cross sections for$np {(I=0)}\to \pi^-pp$ and$ pp\to\pi^+d $ . This approximation is obtained in the present formalism by considering the imaginary part of the two nucleon propagator:$ \begin{aligned} & \frac{1}{M_{\mathrm{inv}}(p_1p_1')-2E_N(p_1)+{\rm i}\epsilon}\\\equiv& {\cal P}\left[\frac{1}{M_{\mathrm{inv}}(p_1p_1')-2E_N(p_1)}\right]-{\rm i}\pi\delta(M_{\mathrm{inv}}(p_1p_1')-2E_N(p_1)).\\ \end{aligned} $

(5) Following this, we have
$ t^{\prime\prime}_\mathrm{on}=-{\rm i}\frac{1}{2}\frac{\tilde{p}_1}{8\pi}\frac{(2M_N)^2}{M_\mathrm{inv}(p_1p_1')}\bar{tt'} , $

(6) where we factorized the angle averaged value of
$ tt' $ ,$ \bar{tt'} $ . Using the analogous expression in Eq. (1) for${\rm d}\sigma_{np\to\pi^+\pi^-d}/ {\rm d}M_{\mathrm{inv}}(\pi^+\pi^-)$ and the on-shell approximation given by Eqs. (6) and (1), we can write the following:$ \begin{aligned}[b] \frac{{\rm d}\sigma_{np\to\pi^+\pi^-d}}{{\rm d}M_{\mathrm{inv}}(\pi^+\pi^-)}=&(2M_N)^2(2M_d)p_d\tilde{p}_\pi\frac{1}{4}\frac{\tilde{p}_1^2}{64\pi^2}\\&\times\frac{1}{M^2_\mathrm{inv}(p_1p_1')}\frac{1}{p_\pi\tilde{p}_1}2|\bar{t}'|^2\frac{{\rm d}\sigma_{np\to\pi^- pp}}{{\rm d}M_\mathrm{inv}(p_1p_1')} , \end{aligned} $

(7) where
$ p_d $ is the deuteron momentum in the original$ np $ rest frame,$ |\bar{t}'|^2 $ is the angle averaged$ |t'|^2 $ , and$ \tilde{p}_\pi $ is the pion momentum in the$ \pi^+\pi^- $ rest frame. In Eq. (7), we assumed that$|\bar{tt'}|^2=|\bar{t}|^2|\bar{t'}|^2$ . Note that the amplitudes$ t,t' $ in [12, 16] have some angular structures, but these are smooth enough to consider this assumption a sensible approximation.Next, we use physical arguments to express the
$ np\to \pi^+\pi^-d $ cross section in the form of an easy compact formula. Note that$ \pi^0\pi^0 $ or$ \pi^+\pi^- $ in state$ I=0 $ , as discussed earlier, require even values for their relative angular momentum l, and when$ l=0 $ ,$ \pi^0\pi^0 $ or the symmetrized$ (\pi^+\pi^-+\pi^-\pi^+) $ behave as identical particles, which revert to a Bose enhancement when the two pions move together. Certainly, if these pions are exactly together, we also have the phase space factor$ \tilde{p}_\pi $ in the term${\rm d}\sigma/{\rm d} M_\mathrm{inv}(\pi^+\pi^-)$ of Eq. (7), which makes this distribution null in the two pion threshold; however, some enhancement for small invariant masses is still expected. Our argument is supported by the results reported in [1, 2] for$ \pi^0\pi^0 $ (see Fig. 2 in [1] and Fig. 4 in [2]) and in [3] for charged pions, although the natures of$ I=0 $ and$ I=1 $ in this case slightly distort the mass distribution compared to the clean$I=0 \;\pi^0\pi^0$ case.We could consider certain
$ M_\mathrm{inv}(\pi^+\pi^-) $ distributions as inputs. However, to make the results as model independent as possible, we set$ \bar{M}_\mathrm{inv}(\pi^+\pi^-)\sim 2m_\pi+60 $ MeV, which is not far from the threshold; however, we varied this value to evaluate the dependence on$ \bar{M}_\mathrm{inv} $ . The stability of the results with varying values of$ \bar{M}_{\mathrm{inv}}(\pi\pi) $ justifies this approximation a posteriori. Thus, we can write$ \frac{{\rm d}\sigma_{np\to\pi^+\pi^-d}}{{\rm d}M_{\mathrm{inv}(\pi^+\pi^-)}}=\sigma_{np\to\pi^+\pi^-d}\delta(M_{\mathrm{inv}}(\pi^+\pi^-)-\bar{M}_{\pi\pi})\ . $

(8) The approximation given by Eq. (8) is sufficiently good and provides a more transparent picture of the reason responsible for the appearance of the peak in the
$ np\to \pi^+\pi^-d $ reaction. In this case, the energy of the two pions is obtained as$ \begin{equation} E_{2\pi}=\frac{s+M^2_\mathrm{inv}(\pi\pi)-M^2_d}{2\sqrt{s}}\ , \end{equation} $

(9) and given that both pions move relatively together, we set
$ E_\pi=E_{2\pi}/2 $ , which allows relating$ M_\mathrm{inv}(p_1p_1') $ with$ \sqrt{s} $ via$ \begin{array}{*{20}{l}} M^2_\mathrm{inv}(p_1p_1')=(P(np)-p_{\pi^-})^2=s+m^2_\pi-2\sqrt{s}E_\pi \end{array} $

(10) and formally
$ \begin{aligned}[b] & 2M_{\mathrm{inv}}(p_1p_1'){\rm d} M_\mathrm{inv}(p_1p_1')\\=&-2\sqrt{s}{\rm d} E_\pi=-M_\mathrm{inv}(\pi\pi){\rm d} M_\mathrm{inv}(\pi\pi)\ . \end{aligned} $

(11) Using this relationship, we can integrate Eq. (8) with respect to
$ M_\mathrm{inv}(\pi\pi) $ , and using Eqs. (2) and (7), we obtain$ \begin{equation} \sigma_{np\to\pi^+\pi^-d}=\frac{M_\mathrm{inv}(p_1p_1')}{4\pi}\frac{\sigma_{np\to\pi^-pp}\sigma_{pp\to\pi^+d}}{M_\mathrm{inv}(\pi\pi)}\frac{\tilde{p}_1^2}{p_\pi p'_{\pi}}p_d\tilde{p}_\pi . \end{equation} $

(12) Here, one last detail is required. As stated, we considered the two step
$ np {(I=0)}\to\pi^-pp $ reaction followed by$ pp\to\pi^+d $ . An appropriately symmetrized$ t^{\prime\prime} $ amplitude requires the addition of$ np {(I=0)}\to\pi^+nn $ followed by$ nn\to \pi^-d $ . Evidently, considering the isospin, the amplitudes$ np {(I=0)}\to \pi^-pp $ and$ np {(I=0)}\to \pi^+nn $ are identical up to the phase of$ \pi^+ $ ($ -1 $ in our formalism), and the same is true for$ pp\to\pi^+d $ and$ nn\to \pi^-d $ for the same configuration of the particles. Hence, the product of the amplitudes is the same. If$ \pi^+ $ and$ \pi^- $ move exactly together, both amplitudes will be identical and will add coherently. However, we observe that the phase space factor$ \tilde{p}_\pi $ in Eq. (12) eliminates this contribution. When considering integration over the five degrees of freedom of the three body phase space, the terms are expected to mostly sum incoherently. Consequently, we must multiply Eq. (12) by$ 2 $ . Similar arguments can be made with respect to the spin sums and averages. Investigations on the$ pp\to \pi^+d $ reaction conducted in [19] indicate the presence of a certain angular dependence on the different spin transitions, and we should expect an incoherent sum over spins. Subsequently, by including the average over initial spins and the sum over final spins in$ |\bar{t}|^2 $ , we would be considering the average over spins of the initial$ np $ and the sum over spins of the deuteron in our formula, in addition to the intermediate sum over the$ pp $ and$ nn $ spins.Equation (12) still relies on the on-shell approximation expressed by Eq. (6). To consider the off shell effects discussed above, we realized that by factorizing the angular averaged
$ t,t' $ amplitudes in the term$ t" $ of Eq. (4) while maintaining their energy dependence as a function of$ M_\mathrm{inv}(p_1p_1') $ , the on shell energy of the intermediate two nucleons (Eq. (4)) presented a remaining structure as the G function of two protons,$ G=\int\frac{{\rm d}^3p_1}{(2\pi)^3}\frac{1}{E_N(p_1)E_N(p_1)}\frac{1}{M_\mathrm{inv}(p_1p'_1)-2E_N(p_1)+{\rm i}\epsilon}\ .\\ $

(13) Following this, we obtain
$ \begin{equation} \mathrm{Im}G=-\frac{1}{2\pi}\frac{\tilde{p}_1}{M_{\mathrm{inv}}(p_1p_1')} \ , \end{equation} $

(14) where, as mentioned after Eq. (1),
$ \tilde{p}_1 $ is the momentum of both protons in their rest frame. The on shell factorization of the terms t and$ t' $ outside the G function has been justified in the discussion following Eq. (3) from different perspectives. We proceed along a different direction with respect to the derivation of Eq. (6): we now retain the two terms in Eq. (5) rather than retaining only the imaginary part. In Eq. (6), we considered the imaginary part of the integral of Eq. (4). This is equivalent to taking$ \mathrm{Im}\,G $ of Eq. (14) instead of G in the integral of Eq. (13). To revert this approximation and approximately determine the effects of the off shell part of the integral, we replace the following in Eq. (12):$ \left(\frac{\tilde{p}_1}{2\pi M_\mathrm{inv}(p_1p_1')}\right)^2\to |G(M_\mathrm{inv})|^2\ . $

(15) The last step in the evaluation of
$ \sigma_{np\to\pi^+\pi^-d} $ requires the use of experimental data for$ np(I=0)\to\pi^-pp $ and$ pp\to \pi^+d $ . We directly extracted$ \sigma_{pp\to \pi^+d} $ from the experiments reported in [16]. For$ \sigma_{np\to\pi^-pp} $ in$ I=0 $ , additional analysis is however required. In [33, 34], the isoscalar$ NN\to\pi NN $ amplitude was obtained via isospin symmetry from$ \sigma_{np\to pp\pi^-} $ and$ \sigma_{pp\to pp\pi^0} $ , and relatively precise results were reported in [12] based on improved measurements of these cross sections. In the erratum of [12] and in [13], it has been clarified that the actual value$ \sigma_{pn(I=0)\to NN\pi} $ is one half that of the value of$ \sigma_{NN(I=0)\to NN\pi} $ reported in [12]. The required cross section is$ \sigma_{pn(I=0)\to pp\pi^-} $ . Thus, using isospin symmetry, we can observe that$ \sigma_{pn(I=0)\to pp\pi^-} $ ,$ \sigma_{pn(I=0)\to nn\pi^+} $ , and$ (\sigma_{pn(I=0) \to pn\pi^0}+\sigma_{pn(I=0)\to np\pi^0 }) $ are all equal. Following this, we express the relationship among the results of [12, 33, 34] as$ \begin{aligned}[b] \sigma_{np(I=0)\to pp\pi^-}= &\frac{1}{3}\sigma_{np(I=0)\to NN\pi} = \frac{1}{6}\sigma_{NN(I=0)\to NN\pi}\\=&\frac{1}{6}3(2\sigma_{np\to pp \pi^-}-\sigma_{pp\to pp\pi^0}) \end{aligned} .$

(16) For the above, we consider the data for
$ \sigma_{np(I=0)\to NN\pi} $ from Fig. 1 in [13]. Notably, statistical and systematic errors have been considered in [12, 13]. To ensure a realistic fit for the data, we also included systematic errors from the uncertainty given in Eq. (16) when using isospin symmetry. We assumed a typical$5$ % violation of the isospin in each of the last two terms of Eq. (16) and summed the errors in quadrature. The systematic errors obtained were of the order of$ 0.5 $ mb in$ \sigma_{np(I=0)\to NN\pi} $ , which were also added in quadrature to the errors reported in [13]. With these errors, we obtained several good fits with reduced$ \chi^2 $ , ($ \chi^2_r $ ), smaller than$ 1 $ . We selected two of these, one peaking on the lower side of$ \sqrt{s} $ and the other on the upper side for the$ np\mathrm{(I=0)}\to NN\pi $ cross section, and we parameterized the cross section as given below.$ \sigma_i=\left|\frac{\alpha_i}{\sqrt{s}-\tilde{M}_i+{\rm i}\dfrac{\tilde{\Gamma}}{2}}\right|^2 $

(17) Here, set I has the following set of parameters:
$ \tilde{M}_1=2326 $ MeV,$ \tilde{\Gamma}_1=70 $ MeV, and$ \alpha^2_1=2.6\left(\frac{\tilde{\Gamma}_1}{2}\right)^2 $ mb MeV$ ^2 $ ($ \chi^2_r= $ 0.50); set II has the following set of parameters:$ \tilde{M}_2= $ 2335 MeV,$ \tilde{\Gamma}_2=80 $ MeV, and$ \alpha^2_2=2.5\left(\frac{\tilde{\Gamma}_2}{2}\right)^2 $ mb MeV$ ^2 $ ($ \chi^2_r=0.52 $ )①. The$ pp\to\pi^+d $ cross section has accurate data, and we parameterize it as$ \sigma_3=\left|\frac{\alpha_3}{M_\mathrm{inv}(p_1p'_1)-\tilde{M}_3+{\rm i}\frac{\tilde{\Gamma}_3}{2}}\right|^2 ,$

(18) with
$ \tilde{M}_3=2165\; {\rm MeV} $ ,$ \tilde{\Gamma}_3=123.27\; {\rm MeV} $ , and$\alpha^2_3= 3.186\times \left(\frac{\tilde{\Gamma}_3}{2}\right)^2$ mb MeV$ ^2 $ .Based on the above discussions, our final formula on shell can be expressed as
$ \sigma_{np\to\pi^+\pi^-d}=\frac{M_{\mathrm{inv}}(p_1p'_1)}{6\pi}\frac{\sigma^I_{np\to NN\pi}\sigma_{pp\to\pi^+d}}{M_{\mathrm{inv}}(\pi\pi)}\frac{\tilde{p}_1^2}{p_\pi p'_\pi}p_d\tilde{p}_\pi,$

(19) with
$ \sigma^I_{np\to NN\pi}=\sigma_{np(I=0)\to NN\pi} $ from [12, 13]. The corresponding results are depicted in Fig. 2.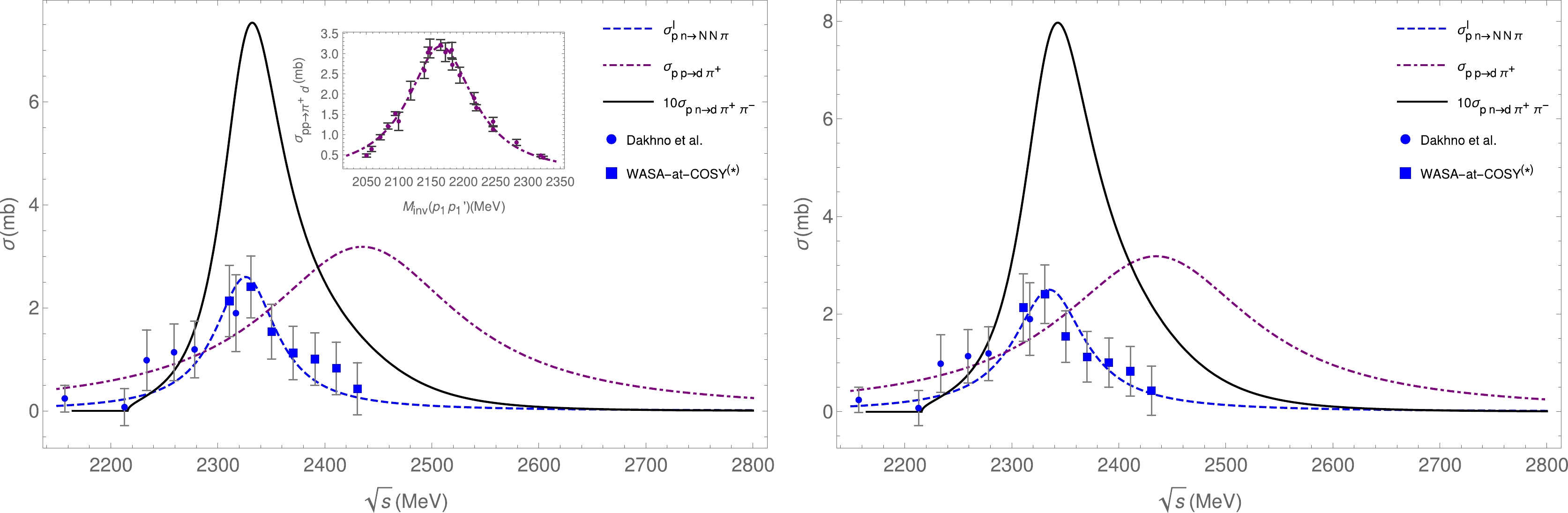
Figure 2. (color online) Plots of
$ \sigma_{np\to\pi^-pp}(I=0) $ and$ \sigma_{pp\to\pi^+d} $ as functions of$ \sqrt{s} $ and$ M_{\mathrm{inv}}(p_1p_1') $ , respectively, where$ M_{\mathrm{inv}}(p_1p_1') $ is evaluated using Eq. (10). The results with$ \sigma_{np\to\pi^+\pi^-d} $ in$ I=0 $ of Eq. (19) are multiplied by$ 10 $ for better comparison. Left: Results for set I. Right: Results for set II.$ \bar{M}_{\pi\pi}=2m_\pi+60 $ MeV. Inset:$ \sigma_{pp\to\pi^+d} $ as a function of$ M_{\mathrm{inv}}(p_1p'_1) $ . Data for$ pp\to\pi^+d $ extracted from [16]. Data for$ np\mathrm{(I=0)}\to\pi NN $ extracted from Dakhno et al. [33] and WASA-at-COSY$ ^{(*)} $ [12, 13], including systematic errors from isospin violation.We can observe that the cross sections of
$ pp\to \pi^+d $ and$np (I=0) \to NN\pi$ overlap around the center of their energy distributions such that their product in Eq. (19) produces a narrow peak around$ \sqrt{s}=2340 $ MeV, which is close to the position of the experimental$ np\to\pi^+\pi^-d $ peak around$ 2365 $ MeV.Table 1 summarizes the results obtained using sets I and II for the strength of
$ \sigma_{np\to\pi^+\pi^-d} $ at the peak, peak position, peak width, varying$ \bar{M}_{\pi\pi} $ , and$ p_{1,\mathrm{max}} $ for the off shell calculations. The results appear stable with changes in$ \bar{M}_{\pi\pi} $ , justifying the use of Eq. (8). Note that the off shell effects resulting from Eq. (15) are small, justifying the on shell approximation used in [8]. The strength at the peak between$ 0.72-0.96 $ mb can be considered good compared to the experimental one around$ 0.5 $ mb, given the different applied approximations (note: the fits to the$ np {(I=0)}\to \pi^-pp $ cross section with systematic errors presenting$ 20\%-30\% $ smaller strengths at the peak are still acceptable; hence, such uncertainties in the resulting$ np\to\pi^+\pi^-d $ cross section are expected). The peak position from$ 2332-2345 $ MeV can also be considered good compared to the approximate peak positions at$ 2365 $ MeV, as experimentally reported previously [1–3, 12]. The narrow width observed in the experiment with$ 70-75 $ MeV is also well reproduced by our results in the range of 75–88 MeV.$\delta\bar{M}_{\pi\pi}/{\rm MeV}$ 

$ p_{1,\mathrm{max}}^{\mathrm{o.s.}}/{\rm MeV} $ 

Set I $ 40 $ 

$ 60 $ 

$ 80 $ 

$ 700 $ 

$ 800 $ 

strength/mb $ 0.72 $ 

$ 0.76 $ 

$ 0.75 $ 

$ 0.82 $ 

$ 0.95 $ 

position/MeV $ 2332 $ 

$ 2332 $ 

$ 2332 $ 

$ 2332 $ 

$ 2332 $ 

width/MeV $ 76 $ 

$ 76 $ 

$ 81 $ 

$ 75 $ 

$ 75 $ 

Set II strength/mb $ 0.75 $ 

$ 0.80 $ 

$ 0.80 $ 

$ 0.85 $ 

$ 0.96 $ 

position/MeV $ 2342 $ 

$ 2345 $ 

$ 2345 $ 

$ 2343 $ 

$ 2342 $ 

width/MeV $ 86 $ 

$ 87 $ 

$ 88 $ 

$ 87 $ 

$ 84 $ 

Table 1. Values of the peak strength ("strength"), peak position ("position"), and width for intermediate particles on shell (columns with
$ \delta \bar{M}_{\pi\pi} $ ,$ \bar{M}_{\pi\pi}=2m_\pi+\delta \bar{M}_{\pi\pi} $ ) and off-shell ("o.s."), where we set$ p_{1,\mathrm{max}}=700 $ and$ 800 $ MeV and$ \delta\bar{M}_{\pi\pi}=60 $ MeV.The appeareance of the peak at approximately
$ 25 $ MeV below the experimental one is not significant given that as discussed in [12], the authors achieved a resolution in$ \sqrt{s} $ with a value of approximately$ 20 $ MeV; in addition, the$ pp\to pp\pi^0 $ and$ pn\to pp\pi^- $ cross sections, based on which$ \sigma_{np\mathrm{(I=0)}\to pp\pi^-} $ is obtained using Eq. (16) with large cancellations, were measured using data bins of$ 50 $ MeV in$ T_p $ .The derivation involves the use of basic ingredients of dynamics in a skilled manner, resulting in some approximations that are reliant on experimental cross sections. It is remarkable that a narrow peak at approximately the correct position, with a strength and width comparable to those of the experimental peak of
$ np\to\pi^+\pi^-d $ , appears despite the considered approximations, and the stability of the results allows us to conclude that a peak with the properties of the experimental one associated with the "$ d^*(2380) $ " dibaryon is unavoidable according to the evaluated mechanism.Based on the fact that the
$ np\to\pi^+\pi^-d $ reaction is involved in the particular reaction mechanism shown in Fig. 1, with a two step sequential one pion production, it is easy to understand why the narrow peak of the$ np\to \pi^+\pi^-d $ reaction cannot be observed for the$ \gamma d\to \pi^0\pi^0d $ reaction, despite the same final state [35]. The first reaction is a fusion reaction, with the last step connected to a triangle singularity. The$ \gamma d\to \pi^0\pi^0d $ reaction is a coherent reaction; here, d is already present in the initial state, and the reaction mechanisms are drastically different. -
In summary, we investigated the reaction mechanism producing a narrow peak in the
$ np\to \pi^+\pi^-d $ reaction cross sections without invoking the "dibaryon" resonance. Based on this perspective, it is easy to understand why the peak is not observed in other investigated reactions, despite the fact that the peak contributing to the inelastic channels of$ pn\to all $ presents traces in the$ NN $ phase shifts, as anticipated in [5, 6] and discussed in [4]. -
Previous studies have claimed the occurrence of the
$ d^*(2380) $ state in other reactions (see review in [4]). Moreover, the results presented in the previous section, posted on arXiv (arXiv: 2102.05575), have been further analyzed in [36], where apparent contradictions with experiments have been reported. In this section, we address the different points raised in [36] to indicate that our approach does not contradict previous experimental results and that the "proofs" presented in favor of the dibaryon hypothesis are unsupported. We follow the points presented in [36] in the discussion below.As mentioned in the previous section, studies on the
$ np\to \pi^0\pi^0d $ and$ np\to \pi^+\pi^-d $ reactions [2, 3] have revealed an unexpected narrow peak in the cross section around$ 2380 $ MeV. This peak has been attributed to a dibaryon, labeled as$ d^*(2380) $ , by an experimental team. It is interesting to note that, based on earlier data pertaining to the reaction, the peak was attributed to a reaction mechanism based on sequential one pion production, that is,$ np\to \pi^-pp\to \pi^-\pi^+d $ together with$ np\to\pi^+nn\to \pi^+\pi^-d $ , in a study conducted by Bar-Nir et al. [8]. The second step,$ pp\to\pi^+d $ , was the object of theoretical investigation in [9–11], and it has been demonstrated to be driven by$ \Delta(1232) $ excitation. We propose a reformulation of the idea of these former works, which has been done in [19] from a Feynman diagrammatic point of view, indicating that the process develops a triangle singularity (TS) [9, 14, 15]. This finding is relevant for the present discussion because it is well known that a TS produces an Argand plot that is similar to the one of an ordinary resonance, even if the origin is a kinematical singularity rather than a genuine physical state [25, 37].The idea adopted by Bar-Nir et al. has been revisited in the former reaction, and with some reasonable approximations and experimental data on the
$ np(I=0)\to pp \pi^- $ and$ pp\to \pi^+d $ reactions, a peak could be obtained for the$ pp\to\pi^+\pi^-d $ reaction; this peak was in qualitative agreement with previous experimental results with regard to its position, width, and strength. Even with the approximations involved and the resulting qualitative agreement, it is important to note that such an agreement, together with the results reported by Bar-Nir et al., is extremely unlikely to be a mere coincidence and hence offers an alternative explanation of the experimentally observed peak.In [36], the authors present a few arguments. We address these arguments as follows.
i) In point 1), the authors note that the error resulting from the proposed approach increases in the
$ pn (I=0) \to \pi^- pp $ reaction. The reason for this increase is that the cross section for this reaction is obtained using isospin symmetry with the following relation:$ \qquad\qquad \sigma_{np(I=0) \to pp \pi^-} = ( \sigma_{np \to pp \pi^-} - \sigma_{pp \to pp \pi^0}/2)\ . $

(20) However, note that this formula involves extensive cancelations, and the result is ten times smaller than each individual term. Thus, we assumed a
$ 5 $ % uncertainty in the terms obtained from isospin violation and determined the errors in the results. These correspond to systematic uncertainties that should have been considered by the experimentalists; however, they were ignored, which is why we accounted for these errors in our analysis. In the high energy region of the spectrum, where the cross section decreases and produces the shape of the cross section, the systematic errors are much greater than the statistical ones. Therefore, the manner in which the statistical errors are summed is inconsequential. The magnitude depends on the systematic errors. In any case, the obtained cross sections are not influenced by these errors.ii) In point 2), the authors claim that our analysis lacked a precise description of the data. With the approximations mentioned above, we cannot possibly pretend to have achieved precise agreements. However, in our opinion, the fact that for such a complicated reaction, we could qualitatively obtain a peak with the correct energy, width, and strength is an accomplishment.
iii) For this argument, first, let us note that in a previous study [19] on the
$ pp\to \pi^+d $ reaction, we proved the dominance of$ ^1D_2 $ , as determined experimentally in [38, 39]. Second, the argument states that because in the$ np(I=0)\to\pi^-pp $ reaction, the invariant mass of$ \pi^-p $ is large, the mass of$ pp $ is small, and it only accommodates$ L=0,L=1 $ waves and not D-waves that are necessary for the overlap of the two-step mechanism. It is interesting to make this argument more quantitative. Let us consider two situations wherein$ M(pp) $ can be easily evaluated. They correspond to the case of$ M(\pi^-p)\vert_{\mathrm{min}}=m_p+m_{\pi^-} $ and$ M(\pi^-p)\vert_{\mathrm{max}}=\sqrt{s}-m_p $ . In the first case, p and$ \pi^- $ move together along a direction opposite to that of the other proton. In the second case, one proton is produced at rest. Note that$ M(pp) $ is trivially evaluated in the foregoing two cases, and for an energy of$ T_p=1200 $ MeV in Fig. 6 of [12], we find the following:a)
$ M(pp) $ (at$ M(\pi^-p)\vert_{\mathrm{min}} $ )$ =2239.47 $ MeV, with an excess energy of the two protons =$ 362.9 $ MeV.b)
$ M(pp) $ (at$M(\pi^-p)\vert_{\mathrm{max}}) =1920.2$ MeV, with an excess energy of$ 43.65 $ MeV.c) Another situation allowing such easy evaluation also exists. This is at the peak of the distribution around
$ M(\pi^-p)=1370 $ MeV, where$ M(\pi^-p) $ from either of the protons is approximately the same and enhances the contribution in this region. Here, we have$2M^2(\pi^-p)+M^2(pp) = s+2m_p^2+m_{\pi^-}^2;$

from this, we obtain
$ M(pp)\simeq 1951 $ MeV corresponding to an excess energy of approximately$ 75 $ MeV for the two protons. Assuming a relative distance of$ r\simeq 2.13 $ fm for the produced two protons, the same as the radius of the deuteron, which corresponds to the range of pion exchange, we determined that the angular momentum,$ L\sim r\times p $ , could reach up to$ L=6 $ in case a),$ L=2 $ in case b), and$ L=3 $ in the most favorable case c).In [36],
$ L=2 $ was already ruled out, and with no calculations, the sequential pion production cross section was deemed to be very small, contradicting the conclusions made in [8]. However, with the dominance of the Roper excitation, as claimed in [36], we could observe that$ S=0 $ for both protons is the dominant mode in$ np(I=0)\to\pi^-pp $ , as in the second step of [19] for the$ pp\to \pi^+d $ reaction, and several L values are allowed. Notably, research along these lines is still underway, given that Roper excitation is not the only ingredient of the$ np(I=0)\to\pi^-pp $ reaction.iv) We would like to state that point 4) is illustrative. Two independent studies, [5] and [6], have proved the existence of a relationship between the
$ pn (I=0) \to \pi^+ \pi^- d $ reaction and the one where the$ np $ of the deuteron emerge as free states. The existence of the peak for the$ pn (I=0) \to \pi^+ \pi^- d $ reaction also consequently produces a peak in$ pn \to \pi^+ \pi^- n p $ and related reactions at the same energy. However, this is the case regardless of the reason responsible for the appearance of the peak in the fusion reaction. This is a key point. Notably, to calculate the cross section of the open reactions, the authors of [36] used the results reported in these references and added the contribution to the results of the standard model, which were also obtained from [7]. Despite the fact that the authors of [5, 6] indicated that the new contribution was necessary regardless of the reason for the fusion reaction, the authors of [36] considered the above as an evidence of a dibaryon.v) In point 5), the authors state that we do not to calculate differential distributions. This is true; however, we did not need the above to prove our points. At the considered qualitative level, we demonstrated that the distribution had to peak at small invariant masses of the two pions because we had two contributions:
$ pn (I=0) \to \pi^- pp $ followed by$ pp \to \pi^+ d $ , together with$ pn (I=0) \to \pi^+ nn $ followed by$ nn \to \pi^- d $ . We could prove that when the momenta of the two pions were equal, the two amplitudes were identical, and they summed to produce a Bose enhancement. In this case, the invariant mass of the two pions has the smallest value. This is why the cross section peaks at a low$ \pi \pi $ invariant mass.vi) Next, the authors claim that the picture proposed by Bar-Nir [8] presented in the former section is not adequate to explain the observed pole in
$ ^3D_3-^3G_3 np $ partial waves. This statement is incorrect. The$ NN $ ,$ I=0 $ phase shifts are affected by the peak in the$ pn (I=0) \to \pi^+ \pi^- d $ reaction because one can have$ pn(I=0) \to \pi^+ \pi^- d \to pn(I=0) $ , where$ \pi^+ \pi^- d $ is in an intermediate state and contributes to the inelasticities. This will be particularly the case in the quantum numbers preferred by the$ pn (I=0) \to \pi^+ \pi^- d $ reaction discussed in our previous papers, in particular the$ ^3D_3 $ partial wave (see the discussion at the end of [19]). At the energy of the peak of the$ pn(I=0) \to \pi^+ \pi^- d $ reaction, the$ np \to np $ amplitude will have an enhanced imaginary part according to the optical theorem. This has an impact on the phase shift at this energy. This can also be stated for most of the reactions claiming to observe the dibaryon. In these reactions, what is actually observed is a consequence of the peak observed in the$ pn(I=0) \to \pi^+ \pi^- d $ reaction, regardless of reason for this peak. This is an important point. The peak of the$ pn(I=0) \to \pi^+ \pi^- d $ reaction will have effects on numerous observables; however, this does not indicate that the reason for the peak is a dibaryon. Nevertheless, it will have consequences. In fact, the effect of the peak of the$ pn(I=0)\to \pi^+\pi^-d $ reaction on the$ ^3D_3 $ and$ ^3G_3 $ partial waves has already been discussed in [5, 6]. Although it appears that the$ pn\to \pi^+\pi^-d\to pn $ process would provide a small contribution to the$ pn \to pn $ amplitude, the relatively large strength of the$ pn \to \pi^+\pi^-d $ peak makes this two step process not too small, as demonstrated in [5, 6]. It is also worth mentioning that small terms in an amplitude can often emerge more clearly in polarization observables than in direct cross sections, as shown in [40].The pole or resonant structure is guaranteed by the triangle singularity of the last step
$ pp\to\pi^+d $ , as shown in [19]. It is well-known that a triangle singularity produces an Argand plot similar to that of a resonance [25, 37].vii) The argument made here is rather weak. The authors mention that "
$ d^*(2380) $ " has been observed in the$ \gamma d\to d\pi^0\pi^0 $ and$ \gamma d\to pn $ reactions. In fact, in [41, 42], one can observe a deviation of the experimental cross section from the theoretical results reported by [43, 44] at low photon energies. These calculations are based on the impulse approximation, and the π rescattering terms are neglected. However, the rescattering contributions of pions are important, particularly at low energies because the momentum transfer is shared between two nucleons, and one picks up smaller deuteron momentum components, where the wave function is larger. Thus, concluding that the discrepancies observed between experiments and calculations based on the impulse approximation are attributable to the dibaryon is incorrect.Let us further extend this discussion. The authors of [41, 42] also studied the
$ \gamma d\to \pi^0 \eta d $ reaction [45, 46]. This reaction was throughly studied theoretically in [47], and the authors discovered that the pion rescattering mechanisms were particularly important, and the most striking feature of the reaction, i.e., the shift of the shape of the invariant mass distributions, was well reproduced. In the$ \gamma d\to \pi^0\eta d $ reaction, η rescattering had a small effect, and only the π rescattering was relevant. In the$ \gamma d\to \pi^0\pi^0 d $ reaction, the two pions could rescatter, making the rescattering mechanism in$ \gamma d\to \pi^0\pi^0 d $ even more important than that in$ \gamma d\to \pi^0\eta d $ .The
$ \gamma d\to \pi^0\pi^0 d $ reaction was measured more accurately in [48]. The same comments can be made with regard to this analysis, given that the comparison with the data was conducted with the impulse approximation in [43, 44]. Notably, in the foregoing study, three dibaryons were claimed to be observed. While it is not the purpose of our discussion to criticize these conclusions, we must point out that a fit to the data with a straight line provides a better$ \chi^2 $ value than the one obtained with three dibaryons.With regard to the
$ \gamma d\to p n $ (or$ pn\to \gamma d $ ) signals observed in polarization observables in [49–51], the following considerations are in order. The cross section for the$ \gamma d\to pn (pn\to \gamma d) $ reaction has a clear peak attributed to the$ \Delta(1232) $ excitation around$ E_\gamma=260 $ MeV [52, 53]. This reaction is similar to the$ pp\to \pi^+d $ reaction studied in [19], which develops a triangle singularity. It is easy to conclude based on the procedure adopted in [19] that the$ \gamma d\to pn $ reaction is also driven by the same triangle singularity. In the cross section, no trace of "$ d^*(2380) $ " can be observed. However, it is well known that polarization observables are sensitive to small terms of the amplitude, which are not present in integrated cross sections [40]. Thus, the combined reaction$ np\to \pi^+\pi^-d\to \gamma d $ provides a contribution to the$ np\to \gamma d $ reaction through an intermediate state with a peak in the "$ d^*(2380) $ " region. As already reported in [40], this small amplitude can emerge in polarization observables, justifying the observation reported in [49–51]. However, this cannot be considered a proof of the existence of a dibaryon, given that it will occur regardless of the reason for the$ pn(I=0)\to\pi^+\pi^-d $ peak.viii) The next point is also somewhat illustrative. The authors claim that the cross section for the
$ pn (I=I) \to \pi^+ \pi^- d $ reaction obtained based on our approach should be approximately$ 4 $ times larger than the one for$pn(I=0) \to \pi^+ \pi^- d$ . However, it is approximately$ 10 $ times smaller according to the experiments. This can be rather easily explained. As mentioned before, the two step process has two amplitudes:$ pn (I=0) \to \pi^- pp $ followed by$ pp \to \pi^+ d $ and$ pn (I=0) \to \pi^+ nn $ followed by$ nn \to \pi^- d $ . For equal momenta of the pions, both amplitudes sum and produce an enhancement in the cross section. By contrast, for$ I=1 $ , we have$pn (I=1) \to \pi^- pp$ followed by$ pp \to \pi^+ d $ and$ pn (I=1) \to \pi^+ nn $ followed by$ nn \to \pi^- d $ . However, in this case, both amplitudes cancel exactly. We have proved this analytically; however, such an explanation is the only possible one because the two pions are in state$ I=1 $ , implying a p-wave, and therefore, they cannot move together.ix) Finally, the comment regarding the Argand plot has an easy explanation. Given that the final step of our mechanism contains a triangle singularity, it creates a structure similar to that of a normal resonance, as discussed in a paper by the COMPASS collaboration [25].
-
We thank Luis Alvarez Ruso for a careful reading of the paper and useful suggestions. R. M. acknowledges support from the CIDEGENT program with Ref. CIDEGENT/2019/015 and from the spanish national grant PID2019-106080GB-C21. The work of N. I. was partly supported by JSPS Overseas Research Fellowships and JSPS KAKENHI Grant Number JP19K14709. This work is also partly supported by the Spanish Ministerio de Economia y Competitividad and European FEDER funds under Contracts No. FIS2017-84038-C2-1-P B and No. FIS2017-84038-C2-2-P B. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 824093 for the STRONG-2020 project.
Sequential single pion production explaining the dibaryon "d*(2380)" peak
- Received Date: 2022-11-08
- Available Online: 2023-04-15
Abstract: In this study, we investigate the two step sequential one pion production mechanism, that is,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: